After all this time, I’m still trying to wrap my head around the idea of massive objects in space as lenses, their distortion of spacetime offering the ability to see distant objects at huge magnification. On Friday we saw how the lensing effect caused by galactic clusters can be used to study dark energy. And consider the early results from the Herschel-ATLAS project, conducted by ESA’s Herschel Space Observatory. Herschel is scanning large areas of the sky in far-infrared and sub-millimeter light. Many of its brightest sources turn out to be magnified by gravitational lenses, where light from a very distant object passes a galaxy much closer to the Earth, bending that light so that the image of the more distant galaxy is magnified and distorted.
Because Herschel has only covered one-thirtieth of the entire Herschel-ATLAS survey area, it’s likely that the project will uncover hundreds of gravitational lenses, offering astronomers the chance to probe galaxies in the early universe that would otherwise be hidden. Thus we learn about the evolution of galaxies from a time when the universe was only a few billion years old, not to mention the possibilities of studying dark matter and its effect on galactic lensing.
Lensing on the Small Scale
Closer to home, we’ve talked a lot in these pages about using the Sun’s gravitational lens for studies of everything from the cosmic microwave background (CMB) to exoplanets around nearby stars. The Sun’s lens is at 550 AU, but the focal line extends to infinity, meaning the spacecraft keeps moving outward while continuing its observation program. In fact, getting beyond 550 AU is a good idea, because it progressively diminishes the problem of solar coronal distortions.
The Tau Zero Foundation is continuing to advocate Claudio Maccone’s FOCAL mission, which would be the first attempt to get a spacecraft to our own Sun’s gravitational lens. In a recent visit, Maccone and I discussed the paper on FOCAL he had delivered at the International Astronautical Congress in Prague. Just as EPOXI’s second cometary pass has shown us how much a spacecraft’s mission can be extended by intelligent marshaling of its resources, so a mission to 550 AU offers up an entirely new set of observations as the vehicle continues to move outward from the Sun. These observations would be progressively more difficult, but they are worth examining for a potential mission trajectory into interstellar space.
For Maccone realized that even as observations of the Sun’s gravitational focus proceeded, a successor to the FOCAL spacecraft could, as it pushed ever deeper into space, tap the lenses of individual planets. The question of planetary gravitational lenses has come up on Centauri Dreams before, and Maccone has now gone into the specifics. If we must reach a minimum of 550 AU to make use of the Sun’s lens, how far do we travel to tap the lenses of the planets?
A Widening Series of Focal Spheres
Jupiter is the most massive planet, and we find that its focal sphere is about 1.1 light months out, or 6100 AU. That’s a useful number to remember, because it’s always possible that the Sun’s coronal effects may distort what we’re trying to look at on the other side of the Sun. If that is the case, we still have a lens at 6100 AU, and that becomes an obvious next target. Beyond this, Neptune’s focal sphere appears at 13,525 AU (2.6 light months). The fact that Neptune is next in line is due to the surprisingly high ratio of the square of its radius to its mass — Maccone demonstrates that the ratio of radius squared to mass is the key factor in this analysis.
Thus Saturn’s lens effect actually comes into play beyond Neptune’s, at 14,425 AU despite the difference in planetary size. As you see, we are now deep into the Oort Cloud, at a distance from the Sun farther than that of Proxima Centauri’s distance from Centauri A and B. Remarkably, the focal sphere of the Earth is found at 15,375 AU, closer than the focal sphere of Uranus, the point being that Earth is the body with the highest density (ratio of mass to volume) in the entire Solar System. Getting to the Earth’s gravitational lens would be useful because we know the composition of our planet’s atmosphere and surface better than that of any other planet. We would thus have maximum data for using its lens for observations.
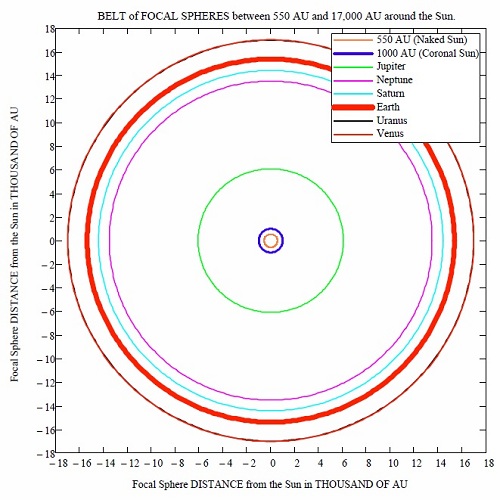
Image: The complete BELT of focal spheres between 550 and 17,000 AU from the Sun, as created by the gravitational lensing effect of the sun and all planets, here shown to scale. The discovery of this belt of focal spheres is the main result put forward in this paper, together with the computation of the relevant antenna gains. Credit: C. Maccone.
A good part of Maccone’s presentation on the matter goes into the question of effective ‘gain’ — Maccone calculates numerical values for the gains at five selected frequencies, from the hydrogen line (1.420 GHz) to the CMB peak at 160 GHz, and evaluates each for planetary gravitational lenses as well as the Sun’s. Clearly, the Sun emerges as our primary target given the poor gain afforded by planets like the Earth, but if future antenna technologies emerge that make it possible to study the weak signatures of the latter, a number of advantages emerge.
The Beauty of Movable Lenses
Obviously, a FOCAL mission that could reach these distances would also qualify as a cometary observer, a spacecraft that would cross the inner Oort Cloud, and that has advantages of its own. But if we can develop the technologies for such a mission, we’ll also have an interesting new take on lensing. For if we start thinking in terms not of a single gravitational lens (the Sun’s) but a series of focal spheres between 550 and 17,000 AU — a series that the spacecraft would cross as it departs our system — then we can take advantage of the fact that we now have a selection of moving targets that paint the background sky with a broader brush.
From the paper:
…while the Sun does not move in the Sun-centered reference frame of the Solar system, all the planets do move. This means that they actually sweep a certain area of the sky, as seen from the spacecraft, so that a spacecraft enjoys a sort of moving magnifying lens. How many extrasolar planets would fall inside this moving magnifying lens? Well, we don’t know nowadays, of course, but the over 400 exoplanets found to date are a neat promise that many more such exoplanets could be detected anew by a suitably equipped spacecraft crossing the distances between 550 and 17,000 AU from the Sun thanks to the gravitational lenses of the planets.
A moving, magnifying series of lenses that we study as the planets sweep out their orbits, on a mission that offers not only observations of distant astronomical phenomena but direct exploration of the Kuiper Belt and the Oort Cloud along the way. Maccone adds:
…looking back to the work done thus far about the possibilities of a truly interstellar flight, it seem fair to say that all planners of the Alpha Centauri missions, in their efforts to reach 277,000 AU, have missed what was at hand at just 17,000 AU. Or, in terms of light time, in order to get all the way to 4.37 light years in a single shot, they have missed what was just three light months away, like the Earth’s focal sphere.
Pushing FOCAL to Its Limits
This is not the FOCAL mission we have discussed in these pages before. That mission is designed to be our first exploration of the Sun’s gravitational lens, one that will demand new developments in propulsion to accomplish its task within a fifty-year timeframe, but one that in the broader scheme of things is reasonably near-term. Think of the ‘moving lens’ mission as a follow-on, a more futuristic concept, one we can consider as a motivator to develop still faster technologies and the hugely sensitive antennae needed to pull down the data, not to mention the sophisticated communications demanded to relay the information back to Earth.
These are ambitious mission ideas, but it’s by thinking about what the universe offers us by way of observation and analysis that we set our goals. From the discovery of new exoplanets to the close study of galactic and extragalactic objects, the crossing of the space between 550 AU to 17,000 AU would be profitable in ways we have not before considered. Evaluate nearby space in terms of lensing opportunities and you begin to see the Solar System and neighboring stars in a different light, one that may even have SETI implications, as we’ll see in an upcoming story.
The paper is Maccone, “A New Belt Beyond Kuiper’s: A Belt of Focal Spheres Between 550 and 17,000 AU for SETI and Science.” I’ll update this with the complete reference when the paper is published.



I have to wonder if I misunderstand how the lensing phenomenon is to be used, because it seems to me the practicalities of causing a spacecraft to maintain a position on a focal sphere in synchrony with planetary motions, in order to conduct observations, would be difficult… especially causing the outbound spacecraft to decelerate sufficiently to use any of these surfaces more than instantaneously as they are crossed.
How much magnification would earth as a gravitational lens provide?
Why are we not using other suns as a way to look at exo-planets?
If a FOCAL mission satellite were in an orbit around the sun at 600 AU would allow a viewing area to ‘sweep’ across the sky as well (at like 1.5 arc-minutes a year). Depending on fuel restrictions, a probe could also actively ‘visit’ different suns by flying into the line that these have with our sun.
What would the ring look like if Jupiter or any other planet was lined up with the Sun as well
Istvan writes:
Remember that the focal line extends to infinity. The spacecraft does not cross the focal sphere and then lose the ability to use the lens. Once past the focal distance, useful observations can continue to be made. This is why the mission to 550 AU assumes continued observations well past the Sun’s gravitational lensing distance.
ant6n writes:
At these distances, the ‘gain’ of the signal is so minuscule that it’s well beyond our capability to pick up. Much the same can be said of planetary signatures like the Earth’s, which is why this is a futuristic concept that would demand major advances in our detection technologies.
Michael writes:
An interesting question, and I’ll have to ask Claudio Maccone about this. Hope I can get an answer for you soon. I’ll also run the other two issues past him — he’s obviously far more qualified to answer them in detail than I am.
A moving field of view could be a real problem for gravitational lensing. The field of view being very small, and at much reduced gain from a planet to boot, we could easily end out with a situation where we’d be lucky to obtain a single photon from a target as it whizzes by. That would be a real showstopper.
Has this been considered?
I once calculated the feasibility to track a moving object, like a planet, and concluded that it is not a big problem. A moving lens, though, is a completely different animal.
To my understanding, objects of greater mass create more gravitational lensing – thus, galaxy clusters exhibit strong lensing, while a nearby star does not give us much. Wouldn’t it make sense to say that using the suns focal line would be by far the best way of conducting astronomy through gravitational lensing? ( at least within our solar system) The planets could be seen as smaller additions to this main lens.
Calling it a focal line helps in understanding the difference between gravitational lensing and optical lensing. However, at great distances, gravitational lensing decreases, right? So, while you could go past the Suns lensing point, would it still be beneficial to go further out? Would the bonus effects of planet lenses offset the distance from the Sun?
In any case, gravitational lensing in the solar system could function as an enormously powerful telescope. I’m sure that making use of this could take our astronomy even further.
Agreed, Eniac. A much better situation would be to orbit a high-mass object with a close-in gravitational focus, an idea that’s been discussed and I’m hunting now for the reference. Of course, that presumes the ability to get to a nearby neutron star or other such object.
bigdan201, yes, absolutely, the Sun is the primary tool for gravitational lensing in our system. One thing about it that is problematic is the possibly distorting corona, which is why Maccone recommends distances greater than the minimum 550 AU to minimize these effects. If we did find that coronal distortions made closer lensing problematic, Jupiter remains a lensing candidate, though obviously at a much greater distance.
Re distance from the Sun, Maccone’s book shows that there are optimum lensing distances for particular kinds of EM radiation. Thus keeping the spacecraft observing as it moves outward in its trajectory is worthwhile. Claudio could obviously explain this better than I can and I wish he weren’t traveling so he could do so, but I’ll see if I can get a comment later.
I see, that makes things clearer. I would definitely appreciate Maccone’s input on the specific constraints and benefits of this.
But regardless of how the details work out, I’m confident that the Sun could work as one of our greatest telescopes. Perhaps it will make it easier to directly image exoplanets, opening up new possibilities in research and discovery.
Hi Guys
The Sun’s putative brown dwarf companion might be even better suited for the job. If it masses in at 20 Jupiter masses then its radius is about ~0.1 Solar and the focal distance is ~110 AU, making it somewhat easier to use than the Sun. Of course if the Sun had a white-dwarf binary companion, obscured for some reason, then it would make an even better gravitational lens…
Perhaps I also misunderstand something here. It seems to me that while we truly do have a Solar focal sphere (that is to say that we could locate a FOCAL mission at any angle in relation to the orbital plane of the solar system), we don’t seem to have a true focal sphere for one or more planets; rather it would be a focal plane or torus: such would be about the same as the plane of the solar system. At least this would be so if we are studying the effects of the interaction of lensing effects of multiple objects within the plane; planets and or Sun. Perhaps my confusion is due to the fact that the planetary minimum lensing distances are centered on the Sun in the illustration.
Are you instead referring to such lenses as centering on each planet? Its true that the Sun’s planetary system at such a resolution as the illustration depicts would seem to be in the same location as the Sun itself.
Hi Again
A 1 solar mass white dwarf has a radius of ~0.01 solar radii. That means its focal distance is just (0.01)^2 * 550 AU = 0.055 AU. Just 8.228 million km from the white-dwarf. The interesting thing is that the atmosphere of a white dwarf is really, really shallow due to its immense gravity, thus the focal distance really is just 0.055 AU. Makes me wonder what the effect would be inside a globular cluster – how intense would the light of all those nearby stars be, focused into a sphere of light, surrounding the white-dwarf?
Enticing notions to be sure, Paul. How does one conjure the result of this imaging, I wonder? How would the images appear, and at what sort of resolution? The images we see now of very distant galaxies behaving in like manner are, to the casual layman, quite difficult to comprehend, even though the scientists among us are quite ecstatic: far away galaxies are mangled, repeated, and radially torn nearly beyond recognition.
Perhaps this is simply the nature of lensing.
A ‘sweeping lens’ such as Jupiter could be useful to ‘sweep across’ an entire neighboring galaxy, particularly Andromeda, revealing a host of exoplanets, even e representative sample in the process.
I understand that the signal (and hence magnification effect) gets weaker with distance, so neighboring stars are poor gravitational lenses, unfortunately.
It is a fascinating thought that a civilization orbiting a (sunlike) star with a neutron star as a binary companion could be exploiting that opportunity as a very nearby and extremely powerful gravitational lense. They would only have to move the space craft a small distance to get different targets into view. Reminds of the book Magnascope.
BTW, an extra added advantage of such a craft at about 600 AU would be the opportunity to do very precise parallax measurements, i.e. direct (triangular) distance measurements.
Dispatcher writes:
Yes, Maccone is looking at the gravitational lensing effects of each planet individually, which could be studied from any position as long as the spacecraft reached the appropriate distance.
and Michael Spencer asks:
High resolutions would be possible with the Sun’s gravitational lens, but I need to have Dr. Maccone answer this re the planets, and I’ll try to have him stop by to do that when his travels slow down.
A bit further to my previous post and Adam’s most recent before mine: if there is a relatively nearby white dwarf or even neutron star between us and the Andromeda galaxy, could such a star be used as a gravitational lens to sample (part of) Andromeda for exoplanets, given its enormous gravitational lensing power and the relatively great distance and ‘density’ of targets of Andromeda?
Sirius B @ 8.6ly might be the closest white dwarf, it is pretty much solar mass and earth size, great for lensing, but 8.6ly is one of the hurdles.
IMHO, 550-700AU solar focal mission sounds interesting, forget about lensing using other planets.
I don’t want this to be taken as in any way questioning the value of the FOCAL proposal or similar missions to the gravitational focus or beyond, but I just had a stray thought about a possible alternative. The idea of the gravitational focus is that it’s the distance at which a gravity-lensed image or signal comes into focus; but as my physicist uncle pointed out to me when I was talking with him about this recently, that image is still detectable from here on Earth, just distorted and out of focus so we don’t get as much information from it. Right?
But that made me think about adaptive optics — about computing the imperfections in a lens or the distortions in an intervening medium and calculating how to correct for them to bring out more clarity in the image. So it occurs to me to wonder: might it be possible to develop a similar technique for gravity-lensed images, a similar way of correcting for the distortion? Maybe then you could bring them into focus without needing to go all the way out to 55o AU or beyond. It might not work as well as actually being on the focal line, but it might work as a cheap-and-dirty alternative.
Or is this analogy completely off-base?
Another possibility would be to use a nearby star as the lens. Are there two fairly close stars in the sky, nearly aligned, such that we could fly into their focal line at a distance of less than 550 au?
Michael,
The “image” is projected along the focal line. The spacecraft would act as the retina of the “big eye”, i.e. consist of an array of detectors. Or just one that is scanning the focal area. A good way to scan is a rotating tether, with the detector(s) traveling along the tether to scan out a spiral. The detectors would only be interested in light coming from the Einstein ring, so optical detectors would be telescopes with an aperture of around 10 cm, which should be enough to resolve the ring and block out sunlight.
Resolution would be extremely good. There are two limits: Refraction and detector size. The latter dominates. A typical nearby star is ~1000 times further than the focus, so a 10 cm detector would cover a 100 m spot on an exoplanet. There are two problems: Because only light through the Einstein ring is gathered, not the full area, there may not be enough light from a planet. The other problem is the anomalous point spread function, which would produce a “glare” which could obscure features and cause starlight to drown out planet light.
As to whether to keep going further out, we don’t have much choice in this matter. We will want to use all our propellant to get there as fast as we can, and will be much to fast then to go into any kind of orbit. As Ronald points out, there are also other very attractive missions for such far-out spacecraft.
Christopher,
This is an interesting thought. However, the lensing effect depends on light from a single point arriving through a large area (the Einstein ring) and then again converging onto a single point. This is not happening closer than 550 AU, and no amount of computing can make up for that, I think.
Parker Shaw’s remark about Sirius B is quite interesting, it indeeb being by far the closest white dwarf at 8.6 ly. 40 Eridani B is the second closest at 16.5 ly.
A neutron star would probably do an even better job at gravitational lensing, but the closest is PSR J0108-1431 at a distance of 424 ly.
Could Sirius B indeed be used as a gravitational lens? Of course the great disadvantage of such a lens is that because of its great distance one would have to move the spacecraft an enormous distance to change target, practically a fixed telescope. Might be most suitable for observing very distant objects, such as a neighboring galaxy. What interesting objects, particularly a galaxy (cluster), are in its line of sight?
I could also turn my previous question around: are there any suitable white dwarfs and/or neutron stars aligned with neighboring galaxies, in particular Andromeda and M33 (Triangulum)?
Ronald writes:
This is so well-timed — at our recent meetings in Austin, the subject of Sirius B was kicked around a good bit in these terms. I’m holding off on going any further into it because I’m trying to get permission to refer to a still unpublished paper on the matter. But expect more later.
If a mission was sent that far out it could also be used for other important observations such as parallax measurements of surrounding stars to high accuracy.
Just have calculated the diffraction limit and found that truly impressive, an order of 10^-11 arcseconds for the visible light is great motivation to go into the Oort cloud…
Besides, this article made me thinking again about space interferometer missions, especially TPF-I-like ones… Since all communication units and precise ion thrusters can be made very small, why are light-collecting satellites so big? Instead, concept of many flat satellites-mirrors made of thin reflecting film with shape controllers flying in paraboloid-like formation may be possible, and about one hundred of them can be launched simultaneously by the single Proton-like launcher. Then another launcher can deliver satellite with beam combiner and detector into the focus, and we have telescope with about 1000 m2 of light collecting area, and extremely versatile and failure-resistant mirror which doesn’t stop working if one of satellites is broken. The diameter of such mirror is bounded, theoretically, only by uniformity of gravitational fields at the location. In Lagrange points it can be many thousand kilometers wide with microarcsecond resolution, and in L4 and L5 – possibly some millions kilometers! More, it can be launched firstly into L2 point, and then sent into L4 or L5, with ability to add another mirrors at any stage if light collecting power isn’t satisfying. It’s the project that could be started “now” and gradually extended for centuries…
Also tried to evaluate the FOCAL concept as a common telescope, and this is what I’ve found:
1) the “diameter” of effective aperture, is about some millions of kilometers, so the resolution limited by diffraction is about 5*10^-11 arcseconds for visible light, if the gravitational perturbations of wavefront aren’t an issue. I can hardly even imagine exoplanetary science with such resolution!! (it’s on order of 1000 meters from one kiloparsec…)
2) huge f-ratio, about 20000:1 for the Sun, so very big detector areas will be needed. For Jupiter it is even much more bigger, along with much more distant focus, and perturbation of wavefront by Sun’s gravity would possibly be the issue.
2,5) “Re distance from the Sun, Maccone’s book shows that there are optimum lensing distances for particular kinds of EM radiation…” That’s not clear, why it is so? as deflection angle isn’t affected by radiation wavelength, then focal lengths for all wavelengths should be the same… And no optical observation of bright gamma ray sources, unless there are filters or different types of detectiors…
3) at any given focus distance, effective aperture is some sort of a thin ring around the Sun, with thickness depending on how much defocusing is allowed, and surface area on order of 10^10 – 10^14 square meters, but that’s very crude estimation since I cannot calculate it directly. Possibly it will depend inversely proportional on needed angular resolution and can be greatly increased with the same resolution by moving outwards on the focal line.
4) for the solar lens and 1000 AU of focal length, the scale of focus plane is 700m/microarcsecond, and 0,01m/(one diffraction limit). So the suggestion is that the best architecture of detectors for diffuse targets such as active galactic nuclei is many independently floating “pixels”, possibly in form of film diodes, each with it’s own sunshield and ion propulsion, or some sort of similar, and more compact arrangement of CCD’s – for exoplanets.
So, for 512*512 pixel image of earth-sized planet 10000 light years away:
20 km/pixel, or 4*10^11 arcseconds/pixel, so the pixel is 3 cm in diameter, and “matrix” is 15 meters wide. Then, assuming 100% detection of incoming photons, 10^10 m2 of effective aperture area, and +41 mag of planet’s brightness (1*10^-24 W/m2), incoming flux will be 1*10^-14 W or ~ 30000 photons per secong of incoming light total, or ~0,05 cps on every pixel, so the exposure of around several minutes would be enough. No hunt for single photons whizzing by, and the planet wouldn’t even have time to rotate! Possibly architecture from Eniac’s November 16, 2010 at 23:53 comment would work very well.
That’s very raw estimation, of course, since as it was posted that each pixel-detector would measure entire brightness of Einstein ring from it’s position, with subsequent deconvolution… alternatively, each detector can have conventional CCD matrix which takes picture of Einstein’s ring and then calculates brightness and spectrum of it’s part at fixed distance from center…
For Jupiter the aperture area will be ~10 times less, and focal plane scale 10 times more, so 1000 times longer exposures are needed. But at the same distances the Sun’s lens effective apperture area will be much bigger!
Nuclear-powered electric propulsion will be needed to get there, and with it there is no need to rely on detector’s orbital motion around the Sun at such distance. Possibly, some sort of mothership with deployable detectors of different types…
torque_xtr: great job! Could you do similar calculations for a planet at 30 ly distance and one at about 3 million ly distance, say in the Andromeda galaxy.
I made a rough estimate myself and came to the conclusion that, if you want to use the white dwarf Sirius B as a gravitational lens at 8.6 ly to use on a target planet in the Andromeda galaxy at about 3 million ly distance, and then next on a different target planet some 3 ly away from the the first one (in a horizontal plane as seen by the observer), one would have to move the craft about 100 million kilometers to get the required angular change. When using the sun as a gravitational lens at 600 AU (about 0.01 ly), one would only have to move the craft about 100 thousand kilometers for the same change of target.
first, let me correct some errors, f-ratio is 59000:1 for 550 AU and it’s increasing proportional to square root of distance. If someone finds another, please correct me…
More, it seemed to me after doing some maths that measuring the part of Einstein’s ring at the selected distance from the center to avoid defocusing is totally useless, since the thickness of the selected part is forbiddingly small
and to build an image of it accurately enough a VERY big telescope is needed at all practical ranges, not only 550 AU… So some sort of deconvolution from whole ring is necessary. If it’s possible, then effective apperture area increases by great factor, with inverse effects on exposure. Bot for such details I guess one should read Maccone’s book :)
at 3 million ly resolution will be ~10000 km/diffraction limit for 1390000 km of aperture, but since effective apperture increases as sqrt(focal_length) for gravitational lens, possibly some detalization can be obtained at thousands of AU (for example, are there continents or single continuous ocean…) But very likely, precise spectroscopical measurements can be done well, due to enormous light collecting power, and all other methods of extraction of data from light curve will be available.
at 30 ly theoretical resolution is on order of tens of meters, as Eniac said, possibly – precise mapping and who knows what else, but the projected “image” is 40 km wide, and the “detector” has to be no smaller. The needed exposure to planet rotation rate won’t be an issue for all cases possibly except very distant “Scattered disc analog” objects with very low surface brightness, due to quadrillions of square meters of light collecting area. Another issue is Sun’s changing radiation and corona into account, as it was said, so I guess that the best focal distance will be much bigger than 550 AU. Also, precise targeting can be possibly difficult. At that focal lengths any uncertainty in planet’s position – and it is projected many thousands kilometers away in the unknown direction from the calculated point… So I hardly can imagine detection of something not previously known by FOCAL method…
Yes, it would be possibly intersting to look at some of the nearest stars’ Einstein rings, with their diameters on order of 50 mas, and white dwarfs’ especially because of their small radius and luminosity, but it will be very difficult to get into some another position on their focal spheres. Probably a search for more luckily aligned white dwarfs in the nearest hundreds of ly will be more effective, say if whide dwarf is at 50 ly and a star with planetary system at 5000 ly and 2 arcminutes away, than 1800 AU away from us they will be perfectly aligned and imaging is possible with great resolution due to ~100 million km of aperture and great focal length…
torque_xtr: very interesting, thanks!