A note the other day from astrodynamics wizard Edward Belbruno (Princeton University) has put me in mind of the ongoing study of the L4 and L5 points being conducted by the STEREO mission. STEREO is a two-spacecraft observatory designed to study solar activity, but in September and October the craft will be making their closest approach to the two gravitational wells at L4 and L5, and it’s possible we’ll discover a resident population of asteroids in the process. If so, we may be looking at material from the birthplace of a long-gone planet.
Call this hypothetical world, as Belbruno does, Theia. We looked at this secondary mission for STEREO last February, but as Belbruno passed along a link to the 2005 paper on the subject of Theia for which he was lead author, it’s time to revisit it. The paper is a lively piece of work, noting that current thinking is that our Moon was the result of a giant impactor, a planetary-sized object that hit the Earth and produced debris that eventually formed the satellite. Formation from the iron-poor debris from the impactor’s mantle helps us explain the Moon’s low density relative to the Earth and also why the Earth and the Moon have the same oxygen-isotope abundances.
That impactor — Theia — is quite interesting. From the paper:
[The theory] explains why Earth and the Moon have the same oxygen-isotope abundances — Earth and the giant impactor came from the same radius in the solar nebula. Meteorites originating from the parent bodies of Mars and Vesta, from different neighborhoods in the solar nebula, have different oxygen-isotope abundances. The impactor theory is able to explain the otherwise paradoxical similarity between the oxygen-isotope abundance in Earth combined with the difference in iron. This is perhaps its most persuasive point.
How does STEREO fit in? The spacecraft will be studying the Lagrange points because it is there that the gravitational pull of the Sun and the Earth balance out, as shown in the diagram below. Belbruno and co-author Richard Gott speculate in this paper that planetesimals could have been trapped in L4 and L5, leading to the accretion of a planet at one of these locations. They point to the Trojan asteroids at Jupiter’s L4 and L5 points and similar objects associated with Mars and Saturn.
Note in the diagram that L4 and L5 allow a unique balance of forces, as explained in the accompanying caption.
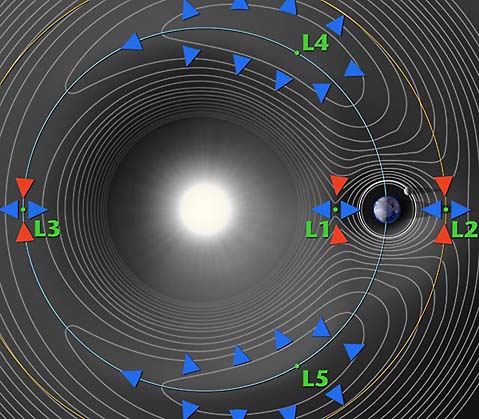
Image: In the above contour plot we see that L4 and L5 correspond to hilltops and L1, L2 and L3 correspond to saddles (i.e. points where the potential is curving up in one direction and down in the other). This suggests that satellites placed at the Lagrange points will have a tendency to wander off (try sitting a marble on top of a watermelon or on top of a real saddle and you get the idea). A detailed analysis confirms these expectations for L1, L2 and L3, but not for L4 and L5. When a satellite parked at L4 or L5 starts to roll off the hill it picks up speed. At this point the Coriolis force comes into play – the same force that causes hurricanes to spin up on the earth – and sends the satellite into a stable orbit around the Lagrange point. Credit: NASA/Neil J. Cornish (WMAP).
But although both L4 and L5 are stable, gravitational perturbations from other planetesimals could eventually cause Theia, our Mars-sized impactor, to escape. The paper examines the mechanisms by which this could happen in considerable detail, concluding with this scenario:
Debris remains at L4 (as the Trojan asteroids prove). From this debris a giant impactor starts to grow like Earth through accretion as described above. As the forming giant impactor reaches a sufficient mass (~0.1mE), it gradually moves away from L4 through gravitational encounters with other remaining planetesimals and it randomly walks in peculiar velocity. It gradually moves farther and farther from L4 approximately on Earth’s orbit in a horseshoe orbit at 1 AU, until it acquires a peculiar velocity of approximately 180 m s-1. The giant impactor then undergoes breakout motion in which it performs a number of cycles about the Sun, repeatedly passing near Earth. In a time span roughly on the order of 100 years, it collides with Earth on a near-parabolic orbit.
Thus STEREO’s ongoing task will be to look for evidence of asteroids at L4 and L5, ancient planetesimals that never became part of the impactor. As this NASA news release from last April notes, telescopic searches from Earth have turned up no such objects, but have only been able to rule out kilometer-sized asteroids. STEREO will be looking at much closer range. As the above diagram shows, the L4 and L5 Lagrange points are actually large regions of space (some fifty million kilometers wide, according to this NASA news release) so the examination will be lengthy.
Public participation is encouraged and you can get involved in the L4/L5 campaign here. Meanwhile, the paper in question is Belbruno and Gott, “Where Did the Moon Come From?” Astronomical Journal Vol. 129 (March, 2005), pp. 1724-1745, available online. More on asteroid detection and its attendant problems on Monday.



>> the Lagrange points are actually large regions of space some fifty kilometers wide
I think they’re wider than this. Fifty thousand kilometers?
Hi Paul
Is the size limit for asteroids in the L points so low?
Got to wonder if Mercury was abraded by a Venusian version of Theia. Or could both Mercury and Mars be “Theias” that got away when Venus and Earth formed?
I guess the L-points might be full of dust and we’d never know from the Zodiacal glow confusing the signal. Seems so strange that such “terra incognita” might be so close to us… that’s what makes exploration fun!
Tom, absolutely right. I left out the critical word ‘million.’ They’re fifty million kilometers wide. I just adjusted the entry for the omission and added a link to a NASA news release on the STEREO mission that uses this number.
Adam, it is indeed fascinating that these exotic places are so close to us, as you say. A mission to an asteroid found here would be made even more interesting by the possibility of checking the oxygen-isotope abundances on these bodies. Assuming, of course, that STEREO finds evidence of them.
If found, would L-point asteroids be easier to get to than NEOs because of lower delta V? Would one make a good 1st manned mission to something further than the moon?
Elon, that’s a good question. Let me see if I can get Greg Matloff’s opinion on this. He’s investigated asteroid missions extensively.
paul,the legrange points are that BIG!!! WOW – how dumb would a person have to be to not see all the cool opportunites!!!!! very very neat and thank you sir for the cool info! your friend george
Missions to the Earth-Sun L4/L5 points would require fairly low delta V, similar to many other asteroid missions. Lagrange missions have other favorable features though. The launch window constraints are small, you can launch pretty much whenever you are ready, whereas with NEO asteroid missions the launch window will tend to be some few number of days every year or more. Similarly, the return launch window is large, allowing for shorter missions (in case of emergency), or extended missions. Also, the mission can be in constant contact with Earth (the Sun will never pass between) and the light time delay will be constant and relatively short (~8 mins).
If there were a sizeable asteroid at either L4 or L5 it would definitely jump to very high on the list of targets for a manned space mission.
Elon has made an excellent suggestion. Accessing an L-point requires a “walking orbit” which usually doesn’t require a lot of propellant. I’ll have to go read my astrodynamics notes on this one.
Hmmm… in one orbit the delta-v is 1655 m/s. Roughly. That’s pretty good. Of course that’s the heliocentric dv, so from LEO it’s a 3.333 km/s burn. Trip time is 1 year… bummer. To do it in six months takes a heliocentric dv of ~3.31 km/s – just 3.7 km/s from LEO. That’s better.
wedge,can not agree more! seems like something we should get done as soon as is possible no foolin! respectfully your friend george
Interesting question is, how we would find out whether there is something in earths L4 and L5 at all. Is the gravity of other planets not enough to kick things out of there ? I mean, jupiter has trojans, does saturn have ones ? If no, maybe the gravity of jupiter is enough to destabilize all lagrange points of inner planets as well, so there is actually no asteroid around our lagrange points ?
Hi All
Seems I messed up my sums. A minimal orbit to the L-points needs to lag or gain on the Earth by 60 degrees in one orbit and the velocity change is tangential to the starting orbit. Thus in heliocentric terms the dv is 0.75 km/s, but applied twice, once to change the initial orbit and once to return to it. Thus from LEO the total dv is ~4 km/s. That’s not bad, but the trip time is 1.167 or 0.833 years, depending on if you’re going to the leading or lagging L-point respectively. That’s not so good. Quicker to flyby Venus or Mars, but then the L-points are ~1 AU away, unlike the ~0.3-0.4 AU to Venus or Mars at their closest.
That’s for a minimal orbital change, in one orbit, which is what automation or big payloads would be sent on. Longer trips, for smaller impulses, can be used, but they’re trickier to design and take multiple years. A quicker trip needs a partial ellipse connecting Earth and the L-point – which takes a lot more heliocentric impulse.
May be a stupid question but someone has to ask it… Why not just aim Hubble at the L4/L5 points and have a look at what’s there, if anything?
Also why would it take so long to get to L4? Why can’t you just escape from earth orbit, then come to a “full stop” and wait for whatever’s at L4 to come barreling up behind you at earth’s orbital speed? Then if you see something you like there, fire up the main engine and go into orbit around it?
Maybe I watch too much Star Trek…
Mark, keep in mind that the Earth is revolving around the Sun at about 30 kilometers per second. If you wanted to let L4 come up behind you, you’d have to kill that velocity first. Not an easy task with today’s technology — the fastest probes we’ve ever built — the Voyagers and New Horizons — move at about two-thirds that speed.
Dual Orion capsules studied for manned asteroid missions (and Lagrangian Points)
BY CRAIG COVAULT
SPACEFLIGHT NOW
Posted: August 17, 2009
A manned asteroid mission using two Orion spacecraft, docked nose-to-nose to form a 50-ton deep space vehicle, is being studied by Lockheed Martin Space Systems as an alternative to resumption of U.S. lunar landing missions.
The Orion asteroid mission concept is being unveiled just as the Presidential committee reviewing U.S. human space flight is citing asteroid missions after 2020 as a less costly alternative to NASA’s proposed lunar landing infrastructure.
Results of the review will be briefed to President Obama by Norman Augustine, committee chairman, by the end of August.
Full article here:
http://www.spaceflightnow.com/news/n0908/17orion/
To quote:
“The presentation also discussed use of single Orion spacecraft to service geosynchronous orbit military and civilian satellites and the potential for them to travel to Lagrangian points to service telescopes like the giant new Webb space telescope set for launch in about four years. Lagrangian points balance out gravity from the sun, Earth and moon allowing spacecraft to remain parked at those locations. They are about 1 million mi. from Earth, about the same distance as some asteroids passing near Earth. This means Orions configured for missions to telescopes, like Webb, at Lagrangian points would have a life support capability also generally suitable for asteroid missions.”
Energy-wise it is easier to escape from the solar system than it is to reach the Sun: the Earth’s orbital velocity is more than half of the solar escape velocity. (For a circular orbit, the orbital velocity is 1/sqrt(2)?71% of the escape velocity from the Sun)
Thus it is easier to get to a star near the ecliptic, for example the Regulus quadruple system than it is to reach the Sun. Unfortunately, the time it would take you to actually get there makes this rather less practicable. (And I said nothing about stopping yourself at the destination either)
One problem with stopping dead – aside from ~30 km/s delta-vee – is one begins falling into the Sun… reaching it in ~64 days. Not healthy.
I looked harder at the short elliptical trips to the L-points… quite fuel intensive. A bit counter-intuitive to design with just pen and paper.
A satellite proposal rom 1962:
http://beyondapollo.blogspot.com/2009/09/libration-point-satellite-1962.html
Mark raises a good point, why can we not point hubble telescpoe. Is something distorting our view from getting a accurate image.