SETI always makes us ask what human-centered assumptions we are making about extraterrestrial civilizations. When it comes to detecting an actual technology, like the starships we’ve been talking about in the last two posts, we’ve largely been forced to study concepts that fit our understanding of physics. Thus Robert Zubrin talks about how we might detect a magsail, or an antimatter engine, or a fusion-powered spacecraft, but he’s careful to note that the kind of concepts once studied by the Breakthrough Propulsion Physics Project at NASA may be undetectable, since we really don’t know what’s possible and what its signature might be.
I mentioned zero-point energy in a previous post because Zubrin likewise mentions it, an idea that would draw from the energy of the vacuum at the quantum level. Would a craft using such energies — if it’s even possible — leave a detectable signal? I’ve never seen a paper on this, but it’s true that one classic paper has looked at another truly exotic mechanism for interstellar travel, the wormhole. These shortcuts through spacetime make space travel a snap. Because they connect one part of the universe to another, you go in one end and come out the other, emerging into another place and, for all we know, another time.
The fact that we don’t know whether wormholes exist doesn’t mean we can’t think about how to detect one, although the authors of the classic paper on wormhole detection make no assumptions about whether or not any intelligent species would actually be using a wormhole. The paper is “Natural Wormholes as Gravitational Lenses,” and it’s no surprise to find that its authors are not only wormhole specialists like Matt Visser and Michael Morris, but physicists with a science fiction connection like John Cramer, Geoffrey Landis, Gregory Benford and the formidable Robert Forward.
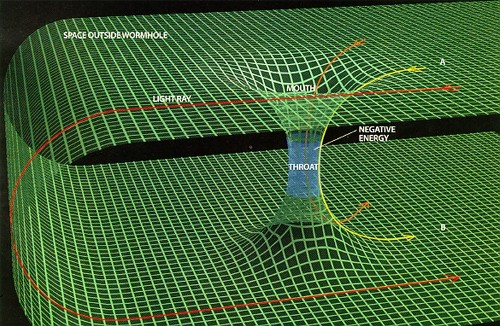
Image: A wormhole presents a shortcut through spacetime. Can one be detected? Credit: Wikimedia Commons.
The analysis assumes that the mouth of a wormhole would accrete mass, which would give the other mouth a net negative mass that would behave in gravitationally unusual ways. Thus the GNACHO (gravitationally negative anomalous compact halo object), which playfully echoes the acronym for massive compact halo objects (MACHOs). Observationally, we can look for a gravitational lensing signature that will enhance background stars by bending light in a fundamentally different way than what a MACHO would do. And because we have MACHO search data available, the authors propose checking them for a GNACHO signature.
In conventional gravitational lensing, when a massive object moves between you and a much more distant object, a greatly magnified and distorted image of the distant object can be seen. Gravitational lensing like this has proven a useful tool for astrophysicists and has also been a means of exoplanet detection. But when a wormhole moves in front of another star, it should de-focus the light and dim it. And as the wormhole continues to move in relation to the background star, it should create a sudden spike of light. The signature, then, is two spikes with a steep lowering of light between them.
The authors think we might find the first solid evidence for the existence of a wormhole in our data by looking for such an event, saying “…the negative gravitational lensing presented here, if observed, would provide distinctive and unambiguous evidence for the existence of a foreground object of negative mass.” And it goes without saying that today’s astronomy, which collects information at a rate far faster than it can be analyzed, might have such evidence tucked away in computer data waiting to be discovered by the right search algorithms.
Would a wormhole be a transportation device? Nobody knows. Assuming we discover a wormhole one day, it would likely be so far away that we wouldn’t be able to get to it to examine its possibilities. But it’s not inconceivable that a sufficiently advanced civilization might be able to create an artificial wormhole, creating a network of spacetime shortcuts for instantaneous travel. Matt Visser has discussed a wormhole whose mouth would be held open by negative energy, ‘…a flat-space wormhole mouth framed by a single continuous loop of exotic cosmic string.’ A primordial wormhole might survive from the early universe. Could one also be created by technology?
Civilizations on the Brink
More conventional means of transport like solar or laser-powered sails present serious problems for detection. In Jerry Pournelle and Larry Niven’s The Mote in God’s Eye, an alien lightsail is detected moving at seven percent of the speed of light, its spectrum the same as the star that it is approaching but blueshifted, which is how analysts have determined it is a sail. The novel’s detection occurs with far more sophisticated observatories than we have in our day, when finding a solar or lightsail in transit would be a tricky thing indeed. A fusion rocket, for example, would emit largely in the X-ray range and could be detectable for several light years, but a lightsail is a highly mutable catch.
I remembered reading something about this in Gregory Matloff’s Deep Space Probes (Springer, 2005) and checked the book to extract this:
If ET prefers non-nuclear travel, he might utilise a laser or maser light sail. If the starship is near enough and the laser/maser is powerful enough, reflections from the sail might be observable as a fast-moving and accelerating monochromatic ‘star.’ However, detection will depend on sail shape and orientation as well as other physical factors.
Therefore, it is not as easy to model the spectral signature of these craft as it is energetic nuclear craft. A starship accelerated using lasers or masers may be easier to detect during deceleration if a magsail is used.
Writing in the comments to yesterday’s post, Centauri Dreams reader James Jason Wentworth recalls Larry Niven’s short story “The Fourth Profession,” which has a lightsail detection something like the one in The Mote in God’s Eye:
“All right. The astronomers were studying a nearby nova, so they caught the intruder a little sooner. It showed a strange spectrum, radically different from a nova and much more constant. It got even stranger. The light was growing brighter at the same time the spectral lines were shifting toward the red.
“It was months before anyone identified the spectrum.
“Then one Jerome Finney finally caught wise. He showed that the spectrum was the light of our own sun, drastically blue-shifted. Some kind of mirror was coming at us, moving at a hell of a clip, but slowing as it came.”
Some sails could be truly gigantic, and we can imagine worldships large enough to require sails the size of a planetary radius, which could be detected when near their home or destination stars, but would be hard to find when in cruise. Matloff goes on to suggest that any search for this kind of ship should look near stars from which an entire civilization might be emigrating. A star like Beta Hydri is a possibility, a nearby (21 light years) solar-type star now expanding from the main sequence. This is the longest shot of all, but finding unusual signatures in visible light near a star leaving the main sequence would at least compel a second look.
The wormhole paper is John Cramer, Robert L. Forward, Gregory Benford et al., “Natural Wormholes as Gravitational Lenses,” Physical Review D (March 15, 1995): pp. 3124-27 (available online). See also Matloff and Pazmino, “Detecting Interstellar Migrations,” in Astronomical and Biochemical Origins and the Search for Life in the Universe, ed. C. B. Cosmovici, S. Bowyer and D. Werthimer, Editrici Compositori, Bologna, Italy (1997), pp. 757-759.



About Lorentz force turning:
“You are wrong. At q/m of 10, you’d have to be skimming the sun’s surface. As you go farther away, you have to increase the charge.”
Indeed. As it turns out, I missed 3 orders of magnitude, underestimating the distance from the Sun you’ll be at (despite saying: At a q/m of 10, you will be so far away from the Sun that you’ll wish you were closer.)
Which means your concept of a light-driven interstellar ship is a failure.
My, concepts, on the other hand:
For the “steam” interstellar ship: passes.
For the light-driven interstellar ship – which has a stationary sail near the Sun, collecting the light and transmitting it to the ship on a Lorentz turning driven by interstellar magnetic fields (for deceleration, see above) – also passed.
“Which is why, as I have said, there is no need for Lorentz turning in this situation. You can pick up the fuel on a straight path just as well.”
You think, Eniac?
This must be why I’ve said in precious posts about the steam interstellar ship concept: “Lorentz turning would be useful, but it’s not necessary in order to accelerate the ship.”
The paper is quite clear on this:
, at equation 14. Multiply 9*10^5 V/m by 10 km, and you get the potential difference between the plates: 9 gigavolts. Independent of the number of times you have stated the contrary.
And, you see, in as much as it does the laws that were good for the plate do no longer apply. A wire behaves like a wire, not like a plate, and that includes the formula for its surface field at the given potential. The plate approximation is only valid at a distance that is large compared to the grid spacing. This should be obvious, and I marvel at your stubborn refusal to understand it.
As I recall, you stumbled upon the idea of Lorentz turning when it became clear that it would be impossible to focus the fuel beam onto the craft over interstellar distances. This remains true. Lorentz turning would have enable us to accelerate the ship without it leaving the solar system, and would have made your scheme somewhat more plausible, although still very far from actually plausible.
Lorentz turning around Jupiter (the only place in the solar system with a suitable field) is still a worthwhile consideration, provided a way can be found to pump energy into the forced orbit, preferably from resources available in the environment. Or, alternatively, using laser or microwave beams (the only kinds of beam that can be collimated to the extent required).
“The paper is quite clear on this”
The paper is clear on the contrary, Eniac.
Meaning, it’s clear in that each 2 grids form a capacitor.
For a capacitor, the electric field between the plates is constant (=charge density/permittivity).
“And, you see, in as much as it does the laws that were good for the plate do no longer apply. A wire behaves like a wire, not like a plate, and that includes the formula for its surface field at the given potential.”
Not according to the paper. But, if you can post/link to papers which supports your affirmation and are more than implausible sounding rhetoric, by all means, do so.
You can even take the 2 grids as being plates with a smallish opening in the center for fuel intake. The mass: ~10^-2 kg/m^2; all 4 grids would weigh only ~3,2 tonnes.
“The plate approximation is only valid at a distance that is large compared to the grid spacing.”
Whitmire even addressed this: ‘To avoid undesirable fringe effects, the grid dimension should be comparable to l1, i.e. 1-10 km.’
I took its dimension to be ~10 km.
“This should be obvious, and I marvel at your stubborn refusal to understand it.”
Eniac, you are the one refusing to accept the evident – such as the ideas described in the quoted paper.
“As I recall, you stumbled upon the idea of Lorentz turning when it became clear that it would be impossible to focus the fuel beam onto the craft over interstellar distances.”
Hardly.
That focus problem was solved first by my lenses (your dictums, again, having no influence on their feasibility – especially since you were unable to come up with a basis for said dictums other than your own incredulity), then by making the travel distance of the pellets very short (by arranging the accelerators in a circle, the ship using Lorentz force in order to turn).
As for the electric field – for the accelerators, it is on the order of 10^4 v/m.
I moved to the steam interstellar ship concept not because the half-circles accelerators were unfeasible, but because they required more resources to build and function.
As for the interstellar dust/interstellar magnetic fields problems – I solved them in the context of the half-circles accelerators by using containers for the fuel.
Finally, with regards to my quote “Lorentz turning would be useful, but it’s not necessary in order to accelerate the ship.”, I wrote it in the context of the steam interstellar ship concept.
“For l1 = 10 km ~6 miles , E = 9 x 105 V/m, at equation 14. Multiply 9*10^5 V/m by 10 km, and you get the potential difference between the plates: 9 gigavolts. Independent of the number of times you have stated the contrary.”
This seems to be the crux of your counterargument.
In a capacitor, the formulas are E=V/d, V=Ed.
For a distance of 10 km, V is 9GV.
Let’s make the 2 grids 1 km distant, without decreasing the beta emitters output – V is 9*10^8.
Let’s make them 1 m distant, without decreasing the beta emitters output – V is 9*10^5.
Or let’s make the 2 grids 100 km distant, without increasing the beta emitters output – V is 9*10^10.
Why this? Have we discovered a way to break conservation of energy?
Hardly.
It’s because the voltage difference between the two plates can be expressed in terms of the work done on a positive test charge q when it moves from the positive to the negative plate.
Work done =Fd; in this context, it means you getting more (or less) out of the voltage you put in a system, NOT increasing said voltage.
E=charge density/permittivity
E=9*10^5 V/m
e=1e0=8,854187817620*10^-12 F/m
This gives charge density=7,96876903586*10^-6 C/m^2
For a grid – a circle with a diameter of 10 km, total charge on the grid Q=625,867120076 C
Capacitance C=e*A/d =6,95407911*10^-8
Voltage V=Q/Capacitance =9*10^9
Hm. You are, indeed, correct, Eniac. I missed the capacitance decreasing with the distance between the grids.
VERY WELL. PLAN B:
A grid made of 10 micrometer wires. The wires have a weight of 10^-7 kg/m; they are positioned 1 cm apart: 100 and 100 perpendicular to the first in a m^2. There are 200 wires per m^2. Mass: 200*10^-7 kg/m2.
A grid has a diameter of 1 km; it has a mass of 15,708 kg.
A capacitor has 2 grids; it has a mass of 31,416 kg. These 2 grids are stationed 10 meters apart.
For decelerating the fuel to the speed of the ship (from the perspective of the ship) I need 1000 such capacitor grids – total mass 31416 kg.
For accelerating the used fuel I need another 31416 kg.
Total mass of the grid capacitors – 62832 kg (62,832 tonnes). The total mass of the ship is 1000 tonnes (meaning, I can afford to make them so heavy).
Now:
E=charge density/permittivity
E=9*10^5 V/m
e=1e0=8,854187817620*10^-12 F/m
This gives charge density =7,96876903586*10^-6 C/m^2
For a grid capacitor, total charge on the grid Q=(7,96876903586*10^-6)*(3,1416*500^2)
Capacitance C=e*A/d =(8,854187817620*10^-12)*(3,1416*500^2)/10
Voltage V=Q/Capacitance =9*10^6 V; achievable with beta emitters.
Note, Eniac – this is for a top speed of the ship (with thorium 232 – 90 protons – as fuel) of ~0,2 c (delta v of 0,4 c).
20 years to Alpha centauri.
The numbers are even more favorable than I have just posted:
Voltage in a capacitor V=charge density*d/e
For E=9*10^5 V/m in vacuum I have charge density =7,96876903586*10^-6 C/m^2.
In vacuum e=8,854187817620*10^-12
Meaning, I can make a grid 10 meters in diameter; a grid capacitor being made of 2 grids separated by 1 meter.
This gives voltage V=9*10^5; easily within the beta emitters’ capabilities.
The weight of the grid capacitors: 0,0015708 kg per grid; 0,0031416 kg per grid capacitor.
The entire fore grid capacitor is 15,708 kg; 31,416 kg for both forward and aft grid capacitors.
That’s TRIVIALLY light (and I could make it even lighter, by making the grids 1 m in diameter).
On plan B: (Aren’t we somewhere near P or Q, already?)
If I understand correctly, your plan B is to stack your 1000 capacitors on top of each other? You must then have missed the inconvenient fact that the gap between two capacitors forms another capacitor with the opposite field direction. Whatever energy an ion loses to one capacitor, it regains in the gap between it and the next.
The voltage requirement is very simple, and there is no way around it: If you want to stop a singly charged particle with an energy of X eV, you need to create a potential of X Volts.
The ramjet paper specifies a gamma factor of 10, at which protons have an energy of 9 GeV. Your velocity requirement is more modest: at 0.1c, a proton has an energy of 100 MeV. Unfortunately, that is still a little more than all but the fastest beta electrons, so beta emitters are just not suitable. If you are talking heavy ions instead of protons, as I think you do, you need 10-100 times higher voltage, putting you right back at ~10 GV or so.
You seem to think that the fact that the fine structure of the grids was not considered in the paper means that it does not matter. That is very naive: Few publications can (or do) claim to have considered everything there is about a problem. Certainly not in the case of a highly speculative problem like this one.
As for links, publications are not necessary. This is elementary physics. I have previously linked to a hyperphysics page treating the electric field around wires. Go and calculate the field around a 10 micrometer wire at 9 GV, and you will find it is on the order that I have indicated, roughly 10^15 V/m close to the surface. If you can show it is substantially less, I will bow my head in shame.
In fact, you do not even need a formula. The applicable rule of thumb is: “field equals potential divided by length scale”. I readily admit that that is all I did to arrive at that number. I am fairly confident of its validity, give or take an order of magnitude.
Error correction:
“The entire fore grid capacitor is 15,708 kg; 31,416 kg for both forward and aft grid capacitors.”
This should be:
The entire fore grid capacitor is 31,416 kg; 62,832 kg for both forward and aft grid capacitors.
“Aren’t we somewhere near P or Q, already?”
You’re not at plan A yourself, Eniac.
“You must then have missed the inconvenient fact that the gap between two capacitors forms another capacitor with the opposite field direction. Whatever energy an ion loses to one capacitor, it regains in the gap between it and the next.”
Eniac, A CAPACITOR HAS 2 PLATES; BEYOND THEM, THE ELECTRIC FIELDS OF OPPOSITE POLARITY ALL BUT NULLIFY EACH OTHER (feel free to check any paper discussing capacitors for confirmation).
If you put 2 such capacitors near each other, there will be 4 plates; 2 adjoining. Between the 2 adjoining plates there’s no electric field to speak of.
If I put 10000 such capacitors near each other (each capacitor having 2 plates; none using common plates), between each 2 adjoining plates there’s no electric field to speak of.
Meaning – no “Whatever energy an ion loses to one capacitor, it regains in the gap between it and the next.”
“Go and calculate the field around a 10 micrometer wire at 9 GV”
A 10 micrometer wire? Not quite, Eniac.
That’s quite different from calculating the field generated 1 meter away by a grid of such wires positioned 1 cm (or 1 mm – I can afford it, weight-wise) from each other.
This is far closer to – go calculate the field generated by a plate – or better, between the plates of a capacitor.
Simply pointing to the formula for the electric field generated by a lone wire just won’t do in this instance, Eniac.
9 GV? Again, not quite, Eniac.
With 1 m capacitors, this is 1*10^5 V.
Error correction:
“With 1 m capacitors, this is 1*10^5 V.”
This should be:
With 1 m capacitors, this is 9*10^5 V.
For finding the electric field generated by a wire mesh, Gauss’s law is adequate (the formula is true for any plane which carries uniform charge per unit area).
The formula is for the electric field is E=charge density/2e0. As you can see, the electric field strength does not decrease with distance (for an infinite plane or for close to a finite one).
For a capacitor with 2 plates with a diameter of 10 m, 1 m apart, it’s an adequate approximation.
No wonder Whitmore, Bussard (which complimented Whitmore’s work), etc didn’t consider this a problem – or bothered with the obvious (for them) demonstration of how a mesh behaves like a “plane”.
If there is no field, then there is no potential difference. That means the adjoining plates are at the same potential, and the voltage adds up across all the capacitors. You are back to 9 GV.
Sure it is different. It is, however, what is required to calculate the surface field. The surface field is what is relevant for field emission, and it is of the order I have indicated.
Except, a wire mesh carries a extremely non-uniform charge per unit area.
Far from the plates, it is. But not near the surface of the wires, where it counts for field emission.
Whitmore and Bussard would never make such a trivial mistake. When you write a paper, you have to watch the scope, and pick your battles. They chose not to go into field emission or tensional stability, for whatever reason.
I said we, didn’t I? :-)
I am not sure what the problem is you are having with the concept that the field at the surface of the wires is different from that between the grids. Are you claiming the field must be the same? Why? That would obviously be incorrect.
Perhaps there is just a misunderstanding of some sort?
“If there is no field, then there is no potential difference. That means the adjoining plates are at the same potential, and the voltage adds up across all the capacitors. You are back to 9 GV.”
?
Eniac, between the 2 plates of any capacitor, the field/potential has a non-zero value. Beyond these plates, the field/potential is essentially 0 (the oppositely charged fields nullifying each other).
AKA
Between the 2 grids of a capacitor (1 m apart), the field is 9*10^5 v/m; the potential 9*10^5 v. If you pot 2 grid capacitors near each other, the field between the adjoining 2 plates (1 belonging to each capacitor) will be 0; the voltage will be 0, too – WHICH IS A GOOD THING, Eniac; I don’t want an electric field there.
“Except, a wire mesh carries a extremely non-uniform charge per unit area.”
Except a wire mesh behaves very much like a plane which carries uniform charge per unit area, if the unit area is 1 m and the grid is dense enough (the wires being 1 cm distant – of course, I can easily make this 1 mm or smaller if so I want).
Meaning, Gauss’s law very much applies – E=charge density/2e0 (no decrease with distance).
Which means, near or 1 m away from the grid the field is 9*10^5 – AKA field emission is not a problem.
All of the above meaning – with my system, the fuel will experience 9*10^5 v/m for 10 km (due to 10000 capacitors placed near each other); for each capacitor, voltage is 9*10^5 v.
“Are you claiming the field must be the same? Why?”
Because Gauss’s law claims just that, Eniac; and it is most definitely not a “trivial mistake”, regardless of what your intuition tells you.
And Whitmore, Bussard and many other scientifically literate critics, of course, knew Gauss’s law – and read Whitmore describe his contraption as a capacitor, calculate the electric field as such, etc.
You, only the other hand, came up only with rhetoric to support the opposite position – highly unconvincing.
“Whitmore and Bussard would never make such a trivial mistake.”
No, they wouldn’t.
And you, again, are proving unable to support with anything but rhetoric the opposite claim.
You know what, Eniac – I came up with figures (Gauss’s law) to support my claim. You came up with nothing except rhetoric.
Come up with figures; rhetoric is worthless when faced with physical laws.
Apparently you did not understand at all what I am saying. So, I will try to put it in as simple of terms as I can, step by step: Say, the first plate of the first capacitor is at 0 V. The second plate of the first capacitor is at 900 kV. The first plate of the second capacitor is at 900 kV, also (remember, no field, same potential). The second plate of the second capacitor is then at 1800 kV (it must be 900 kV higher than the other plate, or else no field). Capacitor three brings that to 2700 kV, and so on. I hope you will understand, even though I skip the other 9997 explanations, that the second plate of the last capacitor needs to have a potential difference of 9 GV compared with the first plate of the first capacitor. I cannot put it in any simpler terms for you to understand.
In other words, we might as well leave out all the intermediate plates, they accomplish nothing and are dead weight. And, unfortunately, we still have to charge the plates to 9 GV.
I more college level physics: Voltage is the same as electrostatic potential, and potential is conservative (this means you have to do the same work, independent of the path you take from one point to another). So, to brake a 9GeV particle to a stop, you need it to go from 0 to 9GV. There is no way to avoid the 9 GV, because the potential is conservative. It does not matter how many grids or funnily curved paths you ask your particle to go through, if it is going to be stopped by the field, 9 GV is going to be the voltage at the point where it comes to rest.
I have already tried to patiently explain that what counts is not the field near the grid, but the field directly at the surface of the wire, and that is obviously much higher than that at distances where the plate approximation is valid. Between the plates, the field is parallel, as you say, but all field lines need to end at the wires, so they have to converge there. I cannot put it in any simpler terms for you to understand.
You did nothing of the sort. This is what you came up with:
Where are the figures? In any case, you are apparently aware that the charge has to be uniform for your argument to apply, which it obviously isn’t, for a grid. This makes it very hard to understand why you persist in your hopeless, nonsensical position.
This is laughable. If you look back, you will see that I beat you at least 10:1 in terms of figures vs. rhetoric.
We are now at a point where you refuse to understand the most basic physical laws and principles. I cannot continue in this manner.
“Say, the first plate of the first capacitor is at 0 V. The second plate of the first capacitor is at 900 kV. The first plate of the second capacitor is at 900 kV, also (remember, no field, same potential). The second plate of the second capacitor is then at 1800 kV (it must be 900 kV higher than the other plate, or else no field). Capacitor three brings that to 2700 kV, and so on. I hope you will understand, even though I skip the other 9997 explanations”
Only if you want to power all your capacitors with one generator, Eniac.
I want to put one generator per each 1 m capacitor – each generator only needing to generate 9*10^5 v for that one capacitor (meaning, beta emitters can do it).
10000 beta emitters will generate the necessary voltage for all 10000 capacitors – without any generator exceeding what’s possible for beta emitters.
And yes, their combined output will go to 9*10^9 V (potential being conservative) – but without any single generator needing to generate this voltage alone (but spread out among 10000 generators), nor any single grid needing to support it (spread out among 10000 capacitors, 20000 grids).
“Where are the figures? In any case, you are apparently aware that the charge has to be uniform for your argument to apply, which it obviously isn’t, for a grid.”
Gauss’s law for for any plane which carries uniform charge per unit area:
E=charge density/2e0.
Take a grid. Take a 1 m^2 square and put it anywhere on this grid; the charge within the 1 m^2 square will be the same. As per the definition, there is uniform charge per unit area. Meaning, the formula applies, as well.
“I have already tried to patiently explain that what counts is not the field near the grid, but the field directly at the surface of the wire, and that is obviously much higher than that at distances where the plate approximation is valid.”
Eniac, the wires are 1 mm distant – AKA, after ~1 mm, Gauss’ law applies.
The electric field is obviously much higher near the wire that at ~1 mm distance from the wire? When the field generated by wires decreases only linearly with distance? Not really.
“If you look back, you will see that I beat you at least 10:1 in terms of figures vs. rhetoric.”
Not quite 10:1, but yes, you did ‘beat me’.
This is a case where I beat you, though.
Eniac, the wires are 1 mm distant – AKA, after ~1 mm, Gauss’ law applies.
The electric field is obviously much higher near the wire that at ~1 mm distance from the wire? When the field generated by wires decreases only linearly with distance? Not really.
For a wire:
E=charge per length unit/2*pi*r*e0
10 microns is 10^-5 meters
1 millimeter is 10^-3 meters
Indeed, at 1 mm, the difference in strength is 2 orders of magnitude – for 9*10^5 v/m at 1 mm distance, I need 9*10^7 v/m near the wires.
Very well. I put the wires 0,1 mm distant:
The entire fore grid capacitor is 3141,6 kg; 6283,2 kg for both forward and aft grid capacitors.
Near the wires have 9*10^6 v/m near the 10 micron wire; 9*10^5 at 0,1 mm distance and between the plates of the grid capacitor.
I am relieved that you finally realized that the wire surface field is much stronger than the “plate” field. Although, I had in my mind a version of the grid with thin wires and a large distance (meters) between them, because that is needed to let particles through and avoid excessive weight. The distance should be smaller than the Debye length of the surrounding plasma, which is around 7 meters in the solar system, if I remember correctly.
That alleviates the surface field issue somewhat. Now, recalculate the mass of your grids. See if it is still reasonable. Also, observe that each grid will now absorb ~11% of the particles impinging on it, which does not augur well for the number of particles that will make it through 10,000 grids. Or for the survival of the grids in the hail of high energy heavy ions.
Luckily, 9999 of them are totally useless, so we can leave them out. The remaining grid, at +9GV, could theoretically stop your fuel atoms before they hit, were it not vaporized by impacting electrons from the surrounding plasma, or torn to shreds by electrostatic repulsion. Whichever happens first, likely within nanoseconds.
The voltage from end to end is 9GV, regardless of the number of “generators”, or their nature.
Absolutely not. Any beta emitter at a positive potential of more than 10-100 MV will have its beta particles loop right back. They do not have enough energy to escape, and they will either be re-absorbed or stick around and shield the charge. Most of your grids are charged well above 10-100 MV, and no beta emitter can keep them charged.
Hardly. I’ll call it even, though, as my 10^15 V/m estimate was clearly too high. The true surface field is equal to the plate field times the ratio of plate area to wire surface area. Fot the 1m/10um grid, then, the surface field would be around 10^11 V/m, 4 orders of magnitude below my estimate, but still about 6 orders of magnitude above what’s feasible.
Ooops, that should be ~19%, of course.
“Most of your grids are charged well above 10-100 MV, and no beta emitter can keep them charged.”
Each grid is charged to 9*10^5 V – below the maximum capacity of beta emitters generators.
Eniac – I take a capacitor with 1 m distance between its plates – and connect it to a 9*10^5 V generator.
I take another capacitor with 1 m distance between its plates – and connect it to another 9*10^5 V generator – on a different circuit.
I repeat this operation 10000 times.
Each generator only achieves 9*10^5 V; each individual 1 m capacitor is powered by only this voltage.
I put these 10000 capacitors one atop each other (resulting a 10000 m long structure); total voltage will be 10000*9*19^5=9 GV – achieved by 10000 9*10^5 V generators.
“Now, recalculate the mass of your grids. See if it is still reasonable.”
I took the component wires to be 10 micron in diameter, placed 10^-4 m from each other (20000 per m^2); the wires’ weight is 1*10^-7 kg/m.
To avoid undesirable fringe effects, the grid dimension should be comparable to the distance between the grids – 1-10 m for 1 m between the grids.
If I take the capacitors to have plates 10 m in diameter – total weight of 10000 1 m capacitors is 3141,6 kg.
If I take the plates to be 1 m in diameter – total weight of 10000 1 m capacitors is 31,416 kg.
As you can see, weight is not a problem.
“Also, observe that each grid will now absorb ~19% of the particles impinging on it, which does not augur well for the number of particles that will make it through 10,000 grids. Or for the survival of the grids in the hail of high energy heavy ions.”
The first grids may absorb ~19% of the particles.
The next grids, not (the absorbtion rate will drop abruptly). Why? As seen from the front of the ship (from the direction the heavy ions have) the wires that make the subsequent grids are placed directly behind the wires that make the first grid.
Also – after going beyond the first grid, the heavy ions will be deflected by the magnetic fields the all charged grids in front of them will have (these grids having an electric charge and traveling at high speed relative to the fuel ions).
When I think beta emission, I think of a beta emitter that generates charge by sending electrons into space, never to come back. You could call this an “open-circuit beta generator”. Those would not work for grids that are charged to more than 100 MV, which is most of them. Perhaps you have some other kind of generator in mind? Please explain.
Really? Would that not negate the shadow effect you were counting on to let ions through? Also, would it not knock the fuel away from the stack of grids entirely?
These grids have gotten awfully small. How was it again that you wanted to lay out the fuel in front of the vessel in a straight line of such precision? Without any of it getting away?
Also, you should calculate the amount of fuel per second you need to collect and the energy deposited by the 20% (at the very least) that won’t make it past the first few grids. Hint: Each atom will deposit 9 GeV of energy. Then, calculate the number of nanoseconds it takes for the grid to reach its boiling temperature.
“When I think beta emission, I think of a beta emitter that generates charge by sending electrons into space, never to come back. You could call this an “open-circuit beta generator”. Those would not work for grids that are charged to more than 100 MV, which is most of them.”
Until we go further, this problem must be cleared.
Each of my 10000 1 m capacitors is charged to only 9*10^5 V (NOT MORE). The total voltage for the 10000 capacitors is 9 GV.
You seem to say that only the first 1 m capacitor can be charged to 9*10^5 V; that the second must be charged to 2*9*10^5;…; the 10000st must be charged to 10000*9*10^5 V.
Eniac, in your configuration, the total voltage of the 10000 capacitors is far, FAR above 9 GV (the last 1 m capacitor alone is charged to 9 GV)
Also, the average electric field of your 10000 capacitors is 5000*9*10^5 V/m – FAR above 9*10^5 V/m.
You seem to think that, after we charged the first capacitor to 9*10^5 V, something would oblige us to charge the second to 2*9*10^5 V, etc.
What?
Each beta emitter is on a different circuit – meaning, it cannot influence the activity of any other beta emitter.
And each capacitor generates NO VOLTAGE AND NO ELECTRIC FIELD outside its plates. Meaning, it CANNOT oblige the next capacitor to be charged to 2*9*10^5 V.
Let’s try a gedankenexperiment:
We have 2 capacitors (1 m thick) – put some distance away.
Each is charged to 2 V (not more, not less), by a separate generator. The electric field of each generator will be 2 V/m.
The combined electric field of the 2 capacitors is 2 V/m (but 2 m of it).
The combined voltage is 4 V – and for this, the second capacitor need not be charged to 4 V; only 2 V, Eniac. You see, the first capacitor did not oblige the second to be charged at a higher voltage in order to function.
You seem to say that only the first 1 m capacitor can be charged to 9*10^5 V; that the second must be charged to 2*9*10^5;…;No, you misunderstand. That is not what I am saying.
This is the correct way of saying it. What you still do not seem to understand fully is that even though each capacitor is charged to 9*10^5 V, because they are connected in series, the absolute potential of each increases by 9*10^5 V until, at the end, the plates of the last capacitor are at the potentials of 9GV – 9*10^5V and 9GV, respectively. Between the plates there is a 9*10^5 V potential difference, meaning the capacitor is charged to 9*10^5 V, as you say. However, both plates are intensely charged (i.e. depleted of electrons) to such an extent that no beta electron would have a chance of escaping.
Your misunderstanding is obvious here. You see, with the two capacitors, the first plate is at 0 V. The second is at 2 V, the third also at 2V, and the fourth at 4V. An electron escaping from the first plate loses no energy. One escaping from the second and third plates loses 2 eV. The one escaping from the fourth plate loses 4 eV. If the electron had started out at 3 eV, say, the one emitted by the fourth plate would simply turn back and be reabsorbed by the plate, being of no help whatsoever in maintaining the charge.
“Between the plates there is a 9*10^5 V potential difference, meaning the capacitor is charged to 9*10^5 V, as you say. However, both plates are intensely charged (i.e. depleted of electrons) to such an extent that no beta electron would have a chance of escaping.”
Let’s take the 2nd – 10000 beta generator as not yet functioning.
Eniac, as I said – Why would both plates of the 2nd – 10000th capacitor be “intensely charged” to more than 0?
There is no voltage/electric current being leaked by the first capacitor, Eniac – nothing whatsoever to charge the second capacitor to above 0. For the second capacitor, the voltage is 0 to 9*10^5.
And so forth.
“You see, with the two capacitors, the first plate is at 0 V. The second plate is at 2 V, the third also at 2V, and the fourth at 4V.”
Again, let’s take the second capacitor’s generator as not functioning. As established, the capacitors are quite some distance away and are…well, capacitors – voltage and electric field does not escape beyond the their plates.
What exactly do you postulate as charging the third plate, Eniac? It’s definitely not the generator of the first capacitor.
“When I think beta emission, I think of a beta emitter that generates charge by sending electrons into space, never to come back. You could call this an “open-circuit beta generator”.”
The electrons are sent by the beta emitter NOT into space, but to the other plate (grid) of the 1 m capacitor.
“Between the plates there is a 9*10^5 V potential difference, meaning the capacitor is charged to 9*10^5 V, as you say. However, both plates are intensely charged (i.e. depleted of electrons) to such an extent that no beta electron would have a chance of escaping.”
Let’s take only the first capacitor as being charged. And the 2nd beta generator (to the 10000st beta generator) is not yet functioning.
Eniac, as I said – In this situation, why would both plates of the 2nd capacitor be “intensely charged” to more than 0?
There is no voltage/electric current being leaked by the first capacitor, Eniac – nothing whatsoever to charge the second capacitor to above 0. For the second capacitor, the voltage – when it will be charged – will be from 0 V to 9*10^5 V.
And so forth from the 2nd capacitor to the 10000st.
“You see, with the two capacitors, the first plate is at 0 V. The second plate is at 2 V, the third also at 2V, and the fourth at 4V.”
Again, let’s take the second capacitor’s generator as not functioning. As established, the capacitors are quite some distance away and are…well, capacitors – voltage and electric field do not escape beyond their plates.
What exactly do you postulate as charging the third plate, Eniac? It’s definitely not the generator of the first capacitor.
Not my postulate. Yours. It is the requirement that there not be a reverse field between the capacitors, which would speed the ions right back up. If the third plate were at 0, then the second and third plate would form a third capacitor charged to the opposite polarity of the other two.
Like this:
| —- d —- | —- l —- | —- d —- |
1) | <– 2V/d — | no field | <– 2V/d — |
4V 2V 2V 0V
1) | | <– 2V/d — |
2V 0V 2V 0V
Anyway, this is just too obvious, I will not discuss it any further.
That is a different beast. Very low efficiency and power density. Can’t be a grid, because most electrons would fly through between the wires, then turn back and return to where they came from. If it’s a plate, it is much too heavy. A lot of electrons would escape at the sides. An RTG with conventional high-voltage generator would be much better.
Rats, looks like WordPress ate part of my beautiful “graphics”. The second configuration was supposed to look just like the first, but with a field of V/l in a direction opposite to the other two fields.
In the middle.
The electrons are sent by the beta emitter NOT into space, but to the other plate (grid) of the 1 m capacitor.
A capacitor looks like this:
E~0 | E=V/d | E~0
As you see, there’s no electric field and voltage beyond the plates/grids.
And, if you add another plate (without charging it):
E~0 | E=V/d | E~0 |
As you see, there is not a capacitor of opposite polarity between plates 2 and 3.
Add another plate, charge the second capacitor and you have:
E~0 | E=V/d | E~0 | E=V/d| E~0
“That is a different beast. Very low efficiency and power density. Can’t be a grid, because most electrons would fly through between the wires, then turn back and return to where they came from. If it’s a plate, it is much too heavy. A lot of electrons would escape at the sides. An RTG with conventional high-voltage generator would be much better.”
D. Whitmore showed in the paper I quoted that the CNO cycle (low energy, as nuclear reactions go) generates the necessary power – 1,25*10^17 W – for charging and maintaining the charge of all 20000 capacitors.
As for the required voltage, 900 KV: this voltage – indeed, voltages higher than this – are already achieved, today.
And about the electrons leaving the wires of a grid and returning to where they came from – what exactly do you name as the cause of this, Eniac?
NOT field emission, that’s for sure.
You see, field emission only becomes a significant at electric fields of 1 GV/m or more (you mentioned above that it happens with electron microscopes at a few volts – this is because the tips of electron microscopes have electric fields of above 1 GV/m at an applied voltage of a few volts).
In my case, the electric field near the wires of the grid is significantly below 1 GV with the wires of the grid arranged 1 millimeter apart:
-for an electric field of 9*10^5 v/m at 1 mm distance from the wires, near the wires the electric field is only 9*10^7 v/m.
Your graphs look much nicer than mine. Alas, you forgot to pencil in the voltages. Remedy this, and your eyes may be opened. Remember, for there to be zero field between two plates, they must be at the same voltage.
Yes, there is enough power. I have said so before. Is this supposed to address my objections, somehow?
Let me repeat as you seem to not have understood: In your proposed beta-voltaic device, the anode cannot be a grid, as most electrons would simply fly through and be wasted. It needs to be a plate, and that would be too heavy. An RTG has better power density and efficiency.
“Remember, for there to be zero field between two plates, they must be at the same voltage.”
They ARE at the same voltage:
Beyond the 2 plates of a capacitor, E~0; V~0 (Remember, V=Ed, Eniac).
As in between two charged capacitors, E~0, V~0.
Here, Eniac:
E~0; V=Ed~0 | E=V/d | E~0; V=Ed~0 | E=V/d| E~0; V=Ed~0
As I already said, the + and – fields nullify each other beyond the 2 plates of an accelerator.
FEEL FREE TO READ THIS IN ANY DESCRIPTION OF HOW A CAPACITOR WORKS.
“In your proposed beta-voltaic device, the anode cannot be a grid, as most electrons would simply fly through and be wasted. It needs to be a plate, and that would be too heavy. An RTG has better power density and efficiency.”
In my system, the power is generated by fission or fusion reactors.
RTGs? I don’t need them.
As for the voltage, voltage in the megavolts range – as said – is already achieved today – by using high-voltage rectifiers, etc.
For how when two plates of different charge are placed near each other, the two E-fields between the plates add while the E-field outside the plate cancel – and, of course, the voltage outside the plates is 0, as well (just to give a link):
http://faculty.wwu.edu/vawter/PhysicsNet/Topics/Capacitors/ParallCap.html
You can find this information in any somewhat detailed presentation of capacitors, Eniac.
PS:
“As I already said, the + and – fields nullify each other beyond the 2 plates of an accelerator.”
This should be:
“As I already said, the + and – fields nullify each other beyond the 2 plates of a capacitor.”
You have annotated the differential voltage between plates. You should annotate the absolute potential of each plate. This is what counts when it comes to beta-emission, Coulombic repulsion, and discharge into the surrounding plasma, i.e. all the things that matter. You will get the following voltages:
v=0 | v=Ed | V=Ed | V=2Ed | V=2Ed | V=3Ed | … | V=10,000 ED (aka 9GV)
Notice how the differential potential between odd and even plates is Ed (your capacitors), and that between even and odd plates is zero (your field-free spaces). You are somehow confusing fields with potentials, or absolute potentials with differential ones, or some such thing that makes you miss the point so stubbornly.
I am also still marveling why you insist on the intermediate plates, when plate 1 and plate 20,000 could do the same job much better, by themselves. Given, of course, you can maintain the 9GV charge (with or without the intermediate plates) for more than the few nanoseconds it would take the grid/plate to disintegrate and/or discharge, which you can not.
Good thing you finally gave up on the betavoltaics. Of course, your nuclear drive would be even better suited to power the thing than RTGs. IF you can keep it fueled, that is.
Eniac
E1,V1 | E2,V2 | E3,V3
– +
That’s a capacitor; one plate – charged, one + charged; 1 m between the plates; electric field between the plates is 900 KV/m.
What is the absolute voltage V1, V2, V3?
What is the absolute electric field E1, E2, E3?
“I am also still marveling why you insist on the intermediate plates, when plate 1 and plate 20,000 could do the same job much better, by themselves.”
Not even close.
To avoid fringe effects, plate 1 and 20000 must be 1-10 km in diameter.
My 20000 plates can be 1 m in diameter (even smaller), and avoid said effects (their total area/weight is much lower).
As for the other reason – I await first your answer to the ‘problem’ I posted above.
That is the first capacitor. On the second, one plate needs to be charged +, the other ++. Then, ++ and +++. Then, +++ and ++++. And so on. Otherwise, you get a reverse field in between. This is not so difficult to understand. Please try harder.
“That is the first capacitor.”
Eniac, I asked you for the specific formulas and numbers.
It’s obvious words alone will not make you understand.
So:
E1,V1 | E2,V2 | E3,V3
– +
That’s a capacitor; one plate – charged, one + charged; 1 m between the plates; electric field between the plates is 900 KV/m.
What is the absolute voltage V1, V2, V3?
What is the absolute electric field E1, E2, E3?
Do write the formulas and numbers for these absolute voltages and electric fields.
Hope the below is enough formulas and numbers for you. I think you can fill in the other 19,981 lines by yourself.
d: length of capacitor
l: distance between proximal plates of adjoining capacitors
plate 1 potential: V1 = 0
field: (V2-V1)/d = 900kV/d
plate 2 potential: V2 = 900kV
field: (V3-V2)/l = 0
plate 3 potential: V3 = 900kV
field: (V4-V3)/d = 900kV/d
plate 4 potential: V4 = 1800kV
field: (V5-V4)/l = 0
plate 5 potential: V5 = 1800kV
field: (V6-V5)/l = 900kV/d
plate 6 potential: V6 = 2700kV
field: (V7-V6)/l = 0
plate 7 potential: V7 = 2700kV
field: (V8-V7)/l = 900kV/d
plate 8 potential: V8 = 3600kV
field: (V9-V8)/l = 0
plate 9 potential: V9 = 3600kV
field: (V10-V9)/l = 900kV/d
….
Look at it as 10000 capacitors connected in series. If each is charged to 900kV, what is the total voltage differential from plate 1 to plate 20,000? Further assume that none of the plates can be negatively charged, because of electron field emission. What then is the minimum absolute positive voltage on the 20,000th plate?
Hint: start with “9” and ends with “GV”
Correction: Some of the l’s in my formulas should be d’s. I think it is clear which ones….
“Hope the below is enough formulas and numbers for you. I think you can fill in the other 19,981 lines by yourself.”
Eniac, the formulas I asked were for a standard capacitor.
Very well. I will write them.
First – the electric field generated by a charged plate alone: E=charge density/2*e0
Now – the electric fields generated by a parallel plate capacitor:
E1,V1 | E2,V2 | E3,V3
– +
That’s a capacitor; ONE PLATE – CHARGED, ONE + CHARGED; 1 m between the plates; electric field between the plates is 900 KV/m.
What is the absolute voltage V1, V2, V3?
What is the absolute electric field E1, E2, E3?
E2= charge density/2*e0 + charge density/2*e0 =900 KV/m (the fields, between the plates of the capacitor, add up)
V2=E2*1=900 KV
E1= -charge density/2*e0 + charge density/2*e0 (the fields, beyond the plates of the capacitor, cancel each other)
V1=0*1=0
E3=charge density/2*e0 – charge density/2*e0
V3=0*1=0
What does this mean?
It means that for any NON-CHARGED object, found beyond the plates of the capacitor, the capacitor will have an electric field of 0 V/m and a voltage of 0 V.
As such, you do NOT have to charge this NON-CHARGED object in order to get no potential difference between it and the capacitor.
What this means for my system?
It means I don’t have to charge the second capacitor’s first plate to 900 KV (forcing me to go to 1800 KV for the next plate) ONLY for there to be no potential difference between it and the charged first capacitor.
If the second capacitor’s first plate is at 0 V, there is NO potential difference between it and the charged first capacitor.
PS – Feel free to verify my formulas in ANY work done on capacitors.
“Further assume that none of the plates can be negatively charged, because of electron field emission.”
What?
No, Eniac: In each of my capacitors, one plate is charged positively and ONE NEGATIVELY.
I told you this repeatedly in my posts – as I have told you this is why I don’t need to charge the second capacitor to 1800 KV, etc.
As for electron field emission FOR ELECTRONS (as in, not protons), this becomes a major problem (AKA it increases sharply) ONLY when the electric field reaches ~1 GV/m (and I am far below this value).
These are for multiple standard capacitors in series. That is what we are talking about, here, still, I assume. Otherwise, please explain what the new situation is.
Here is your problem: This is actually V1 = 0*1 + C, with C an arbitrary constant.
The field is zero between any two plates at the SAME voltage, that voltage does not have to be zero.
If V1 and V3 were both zero, as you say, there would be no voltage difference across the capacitor, and thus no charge and no field.
It is now clear that you have no understanding whatsoever of the relationship between fields and potentials. You should read up on the subject. This here might be a good starting point: http://en.wikipedia.org/wiki/Electric_potential
“It is now clear that you have no understanding whatsoever of the relationship between fields and potentials.”
Actually, it’s becoming clear that you have no understanding whatsoever of the electric fields and voltages in a standard capacitor, Eniac.
For example:
“If V1 and V3 were both zero, as you say, there would be no voltage difference across the capacitor, and thus no charge and no field.”
Between the plates of the capacitor V2 is not 0, Eniac; the electric fields there add up AKA there is non-zero voltage.
Beyond the plates of the capacitor, the electric fields cancel each other AKA V1 and V3 are 0.
I already gave you a link. Actually look it up before coming with such basic mistakes:
http://faculty.wwu.edu/vawter/PhysicsNet/Topics/Capacitors/ParallCap.html