Back when I was working on my Centauri Dreams book, JPL’s James Lesh told me that the right way to do communications from Alpha Centauri was to use a laser. The problem is simple enough: Radio signals fall off in intensity with the square of their distance, so that a spacecraft twice as far from Earth as another sends back a signal with four times less the strength. Translate that into deep space terms and you’ve got a problem. Voyager puts out a 23-watt signal that has now spread to over one thousand times the diameter of the Earth. And we’re talking about a signal 20 billion times less powerful than the power to run a digital wristwatch.
Now imagine being in Alpha Centauri space and radiating back a radio signal that is 81,000,000 times weaker than what Voyager 2 sent back from Neptune. But lasers can help in a major way. Dispersion of the signal is negligible compared to radio, and optical signals can carry more information. Lesh is not a propulsion man so he leaves the problem of getting to Alpha Centauri to others. But his point was that if you could get a laser installation about the size of the Hubble Space Telescope into Centauri space, you could send back a useful datastream to Earth.
The probe would do that using a 20-watt laser system that would lock onto the Sun as its reference point and beam its signals to a 10-meter telescope in Earth orbit (placed there to avoid absorption effects in the atmosphere). It’s still a tough catch, because you’d have to use optical filters to remove the bright light of the Alpha Centauri system while retaining the laser signal.
But while the propulsion conundrum continues to bedevil us, progress on the laser front is heartening, as witness this news release from Goddard Space Flight Center. Scientists working with the Lunar Reconnaissance Orbiter have successfully beamed an image of the Mona Lisa to the spacecraft, sending the image embedded in laser pulses that normally track the spacecraft. It’s a matter of simultaneous laser communication and tracking, says David Smith (MIT), principal investigator on the LRA’s Lunar Orbiter Laser Altimeter instrument:
“This is the first time anyone has achieved one-way laser communication at planetary distances. In the near future, this type of simple laser communication might serve as a backup for the radio communication that satellites use. In the more distant future, it may allow communication at higher data rates than present radio links can provide.”
The Lunar Reconnaissance Orbiter, I was surprised to find, is the only satellite in orbit around a body other than Earth that is being tracked by laser, making it the ideal tool for demonstrating at least one-way laser communications. The work involved breaking the Mona Lisa into a 152 x 200 pixel array, with each pixel converted into a shade of gray represented by a number between 0 and 4095. According to the news release: “Each pixel was transmitted by a laser pulse, with the pulse being fired in one of 4,096 possible time slots during a brief time window allotted for laser tracking. The complete image was transmitted at a data rate of about 300 bits per second.”
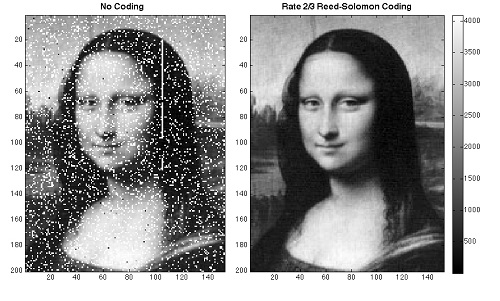
Image: NASA Goddard scientists transmitted an image of the Mona Lisa from Earth to the Lunar Reconnaissance Orbiter at the moon by piggybacking on laser pulses that routinely track the spacecraft. Credit: NASA Goddard Space Flight Center
The image was then returned to Earth using the spacecraft’s radio telemetry system. We’ll soon see where this leads, for NASA’s Lunar Atmosphere and Dust Environment Explorer mission will include further laser communications demonstrations. The robotic mission is scheduled for launch this year, and will in turn be followed by the Laser Communications Relay Demonstration (LCRD), scheduled for a 2017 launch aboard a Loral commercial satellite. LCRD will be NASA’s first long-duration optical communications mission, one that the agency considers part of the roadmap for construction of a space communications system based on lasers.
If we can make this work, data rates ten to one hundred times higher than available through traditional radio frequency systems can emerge using the same mass and power. Or you can go the other route (especially given payload constraints for deep space missions) and get the same data rate using much less mass and power. The LCRD demonstrator will help us see what’s ahead.
In any case, it’s clear that something has to give when we think about leaving the Solar System. Claudio Maccone has gone to work on bit error rate, that essential measure of signal quality that takes the erroneous bits received divided by the total number of bits transmitted. Suppose you tried to monitor a probe in Alpha Centauri space using one of the Deep Space Network’s 70-meter dishes. Maccone assumes a 12-meter inflatable antenna aboard the spacecraft, a link frequency in the Ka band (32 GHz), a bit rate of 32 kbps, and forty watts of transmitting power.
The result: A 50 percent probability of errors. We discussed all this in these pages a couple of years back in The Gravitational Lens and Communications, so I won’t rehash the whole thing other than to say that using the same parameters but working with a FOCAL probe using the Sun’s gravitational lens at 550 AU and beyond, Maccone shows that forty watts of transmitting power produce entirely acceptable bit error rates. Here again you have to have a probe in place before this kind of data return can begin, but getting a FOCAL probe into position could pay off in lowering the mass of the communications package aboard the interstellar probe.
Whether using radio frequencies or lasers, communicating with a probe around another star presents us with huge challenges. James Lesh’s paper on laser communications around Alpha Centauri is Lesh, C. J. Ruggier, and R. J. Cesarone, “Space Communications Technologies for Interstellar Missions,” Journal of the British Interplanetary Society 49 (1996): 7-14. Claudio Maccone’s paper is “Interstellar radio links enhanced by exploiting the Sun as a Gravitational Lens,” Acta Astronautica Vol. 68, Issues 1-2 (2011), pp. 76-84.



Forgive my ignorance, but I’ve always wondered about this. How can you shine a laser at an object that is four light years away? When we look at Alpha Centauri in the sky (or when a hypothetical being on Alpha Centauri looks at our Sun), we are looking at an object that was in that position four years ago. Wouldn’t we need to direct the laser to the future (2017) position of Alpha Centauri? Or would it be in roughly the same place, given the relative movement of the two bodies?
‘It’s still a tough catch, because you’d have to use optical filters to remove the bright light of the Alpha Centauri system while retaining the laser signal.’
Attempting in 1979 to range to the Apollo deployed corner cube reflectors on the moon, we employed a 1 Å (0.1 nm) filter at the wavelength of our Nd YAG laser, 532 nm, to block ambient light (moonlight). The moon, even with such a narrow filter, overwhelmed our 300 mJ, 5 ns pulse, which was returned to a 1 m telescope and PMT. A tough catch indeed!
This document talks about our (improved) system (warning PDF): http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19800004154_1980004154.pdf
Out of curiosity I did a quick calculation. Hopefully I didn’t make any big errors.
For a laser with a nice, wide collimated planar beam (about 10x wider than a typical gas laser), the beamwidth is ~0.01 degrees. The directivity gain would be ~85 dbi.
For the equivalent directivity gain a (perfect) parabolic radio dish operating at 10 GHz would have to be ~240 meters in diameter. The required diameter increases rapidly for lower frequencies.
I kept ignoring this Mona lisa to the moon story in the press because i misunderstood the grossly oversimplified headlines. Really these laser communications are way overdue. Thank you for bringining it into its proper role here on CD. Laser transmit signals from deepspace probes to be intercepted by geostationary satellites to transmit to earth would give us seamless high speed communications with our hardware in deep space. this will be ABSOLUTELY required for high resolution infrared / visible surveys from space telescopes in laGrange point orbits.
As for communications of info over interstellar distances consider sending back DNA
http://www.bbc.co.uk/news/science-environment-21145163.
This same material approach might be used to archive historical information for future humans as deep space Libraries.
What is interesting in laser is the so called gaussian beam, you can have a gaussian beam with radiofrequencies, no matter. The reality is that you can not have an amplitude bigger than the number of sources divided by the distance, so to have a significant light far away, it’s always the same problem, you need a lot of sources. Laser manage to have a lot of small sources synchronised, but it’s all electromagnetism, cavity is a big responsible. (and cavity as a reflector is a source). In a gaussian beam the intensity also falls in 1/r² but from the waist that can be very far from the laser output. The waist is a focus point that exists only because of interférences.
The first poster is a different Mike then me. Not that he doesn’t ask a valid question. Only 4.3 years of proper motion will not have shifted the relative positions of Sol and Alpha Centauri enought that a laser would miss. Even a laser beam will spread out after travelling 4.3 light years.
Mike, here’s what I believe is an understandable and intuitive way of determining this. No equations required.
ACen has a proper motion. This means that it appears, from our perspective to slowly but surely move across the sky. So you are correct that this does involve an aiming issue. Now let’s try it out.
You have a spacecraft. It travels sub-light speeds of course. At slow speeds you can ignore relativistic effects so that it becomes a simple ballistics problem. Now let’s try the same trip goes faster and faster, and faster again.
In the limit as you approach c (which you’ll never reach), the trip time (proper time, as measured by those in the spacecraft) approaches zero. Yes, you can do this, but it takes a lot of energy. Let’s assume that’s taken care of.
The magnitude of the proper motion keeps getting smaller the faster you go, so the course correction gets smaller and smaller. Now become a photon. A photon travels with zero elapsed time (null curve). Therefore you can aim your photon to where you see the photons from ACen (its apparent position) and you will hit your target.
Lots of detail omitted, but that’s the idea.
A solar pumped laser would be ideal for a probe to Alpha Centauri. Typically high powered, as high as 300 watts, and no need to carry a power source.
I would have thought that if you could get a probe to Alpha Centauri that finding a few spare kW or more for the transmitters is not going to be a problem.
Assuming that an in situ mission has reached alpha Cen, another way to get signal back
is to install on board ” Venetian curtain”-like screens which can filter a part of the stellar
light in a modulated way, controlled on board to transmit information. A kind of interstellar morse.
This screen would then be imaged from the solar system with a very high angular resolution, thanks to
a 10,000 km wide hypertelescope in space (as designed by A. Labeyrie).
See http://arxiv.org/abs/1010.2038 for details.
Thanks (especially Ron S. and the other Mike) for helping answer my question. I’m not a physicist, but it helps me understand how this would work!
schneider:
The problem with this otherwise smart approach is the size of the screen required. It would have to be the size of a large planet to make a detectable difference in the light curve of the star.
I’m sorry, but I think Ron S is wrong. If you aim your laser at where Alpha Centauri was four and a bit years ago you’d miss it. It is easy enough to calculate where Alfa Cen will be in 4..36 years, but you can’t ignore proper motion because of null geodesics. What would happen if it met a black hole and swung off in a different direction?
Steve, a photon does not experience spacetime as us slowpokes do. For a photon there is no 4.36 years. In fact there is no time or space interval for a photon between its emission and absorption events. ACen is simply ‘right there’.
No, you still have to point the laser at where Alfa Cen will be, since it has moved more than eight billion kilometers since the light that we see left it.
On top of that, each component of the star is orbiting the barycentre at its own speed- how can your photon predict where to go in the orbit to hit the right star?
Mike(2); a two metre laser would spread out to a footprint of ten or fifteen million kilometers at Alpha Centauri; if the star has moved eight billion kilometers, you will miss it unless you know exactly where it is. Fortunately the proper and orbital motion of these three stars are all well-known.
Steve… what can I say. Believe that if you will.
Well, I am perfectly willing to accept your premise, but you need to explain it a bit more. How can you expect to hit a moving target with a laser unless you calculate where it will be, rather than where it was. I’m quite au fait with concepts like abberation and geodesics; but they don’y absolve you from aiming the laser.
Imagine that the star was only 1AU away, instead of four light years, and traveling at 50% of the speed of light. We would see it pass by very quickly, but do you still recommend that we point our lasers towards where it was rather than where it will be? in the time a photon travels to us and from us to the star to the star it will have traveled 1AU, and would be 60 degrees away from where we first saw it.
Steve, no, aberration does explain it.
http://en.wikipedia.org/wiki/Relativistic_beaming
“Aberration is the change in an object’s apparent direction caused by the relative transverse motion of the observer. In inertial systems it is equal and opposite to the light time correction.”
This particular extract doesn’t say it, but the aberration is in the direction of the star’s proper motion (motion transverse to the observer).
Human intuition can be an encumbrance at times.
Thanks!
However that link doesn’t discuss sending beams to other systems; you still have to aim you laser to where the star will be. Have you given any thought to my 50% c example, where the star would be 60 degrees away from where it appears to be?
Steve, I think I already answered that. Aim along the direction of the received photons (apparent position) and you’ll hit the target. Note the constraint of inertial systems.
Keep in mind (and as I’ve already written earlier, using different words) that the target of your laser *cannot* undergo any dynamical evolution, from the perspective of the photon. It doesn’t simply “slip away” during photon flight.
So if you want a quantitative answer, calculate the aberration for your example and you’ll know where to aim your laser. But then you’ll be looking right at the target anyway when you fire away. :-)
Ron S: I am also not following your reasoning. I am uncomfortable with putting myself into the shoes of a photon, and I do not see how that proves anything about where you would aim. Let me instead imagine myself as a distant observer, stationary with respect to Earth: I see a photon going in a straight line from Alpha Centauri to Earth. I see a beam generated in response, according to your recipe, going back in exactly the opposite direction, and therefore going back through the same point where Alpha Centauri was 8 years ago. Only, Alpha Centauri is not there anymore. What gives?
I think you are wrong; you cannot possibly hit a target 60 degrees away from where you aim it, one which has already passed you and is now moving away in the opposite direction. The aberration of light coming from a moving target seems completely different to the aberration of light chasing after that object after it has passed you. It may be the case that you are correct, but you haven’t demonstrated that yet.
@Steve: Huh? There is only one type of “aberration”. But, really, all I will say since you do not believe me is to ask someone you do trust, or (better) to do the calculation yourself. I gave one limited reference (Wikipedia) but there are ample texts available, several of which are on my bookshelf. By doing so it should be a simple matter to prove me wrong. I don’t have the patience to step through the math and geometry of a precise example, besides which you will gain greater understanding by working through it yourself.
@Eniac: Same thing, except to say there is no need to complicate matters by adding another observer and therefore a third reference frame among which you need to do the appropriate transformations. In any case, no observer will “see a photon going in a straight line”. So I don’t think that helps.
I can understand aberration when the photon is coming *from* Alpha Centauri; because Alfa Cen is moving transversely across the sky,
the beams from there aimed at Sol have to be aimed to the rear of where Sol really is, so that they will travel transversely to where it receives them. This makes the angle at which they are received equal to the angle at which Alfa Cen would appear if we could see where it really is. In other words the aberration is equal to the light time correction.
However, as far as I can see, that doesn’t happen when you are beaming towards a target moving away from you; you have to aim *in front* of where Alfa Cen appears in the sky, so that the beam will appear to arrive at Alfa Cen from Sol’s true position.
In other words, aberration is only equal to light time correction for received messages, not for transmitted ones.
Ron S says “you will gain greater understanding by working through it yourself”. And when I do It comes out just as Ron says, but in the wrong direction. So we should use twice Alpha Centauri’s apparent motion multiplied by the light travel time to compensate from its current position.
@Steve: One word — reciprocity. All observers are equal. The same operation works just fine from AC when the photons come from us.
@Rob: You may want to check your math. Just for the heck of it I pulled a text off my shelf (D’Inverno) and looked up the general aberration equation. (Just in case an error crept into Wikipedia.) I like D’Inverno for its casual approach to this sort of question. For example, he talks about the ‘true’ position of the photon source (he deliberately puts true in quotes) while knowing full well this is a somewhat silly thing to say.
The generalized aberration equation is: tan a’ = sin a / (cos a – v/c), where ‘a’ (actually it’s theta in the book) is the inclination off the horizontal. For transverse motion (which is our particular situation), ‘a’ is 90 degrees. It is therefore a simple bit of algebra to simplify the equation to: a’ = c / v.
I did not look up AC’s proper motion, instead opting to substitute a nominal value of 10 km/s. The value doesn’t matter since it should work for all proper motions for stars at any distance.
Doing this I get an apparent position of ~89.99809 degrees. In other words, if AC is sliding to my (nominal) left I see its apparent position shifted in the opposite direction (nominal right), toward my direction of travel (relative to AC, of course).
If you do the calculation of the proper motion of AC over 4.26 years, it works out to 8.8 AU of transverse motion. Doing the trigonometry (arctan of 8.8 / 264100) the apparent shift in AC’s position is ~0.001909 degrees to the left.
I’ll leave the final bit of arithmetic to you.
Despite all of this please do keep in mind that there is no ‘true’ position of AC nor ‘true’ time that is synchronized to Earth clocks. It’s all just measurements. Regardless of where you decide that AC ‘really is’, if you send an EM message to AC and a response is immediately sent back, the Earth-measured interval is 8.52 years and AC will have shifted 0.003818 to the left. Just as it should. And, again, we aim our laser at the apparent position of AC and the received photons appear to come from the 8.52 years later apparent position of AC.
With that, I’m done with this topic. Anyone who wants to understand in more depth should by all means pick up a text for some self-directed learning. Considering why we’re all here on this blog relativity is both relevant and interesting. Just leave your intuition behind.
That’s because you have to adjust for light travel time/ aberration when considering the light coming from Alpha Centauri. I think you are probably right.
Here’s a puzzle for you all. Let us send a light signal to Alpha Centauri, then immediately return one to Sol.
Now, as measured from a reference frame in Alpha Centauri, the signal must have come from our proper motion x beam time off its current position, and must be sent that much ahead again for the return.
As measured from Sol’s reference frame, the beam goes straight there, and the return straight back. The angle between beams is zero. But this cannot be! Surely they must at least aim our proper motion x travel time ahead. When we calculate the effect of aberration on the observer we find that it is the same size. Commonsense tells us that these two effects must then cancel out since an angle of zero must be invariant under any sort of transformation. Thus we think we can tell them to point in the direction of Sol’s light and transmit.
So which is right?
Ron: “It is therefore a simple bit of algebra to simplify the equation to: a’ = c / v.”
Yikes. I did the math correctly but mistyped the equation. It is obviously: a’ = arctan(c/v). Although it’s also true that, if we’re working in radians, for small angles my error is in fact an excellent approximation.
(Incidentally my comment ‘I think you are probably right’ was actually directed at Rob, rather than Ron S; some sort of aberration of posts diverted it so that it appears to have been directed at Ron S).
It seems to me that the ‘aberration = light travel time’ phenomenon is actually *caused* by the fact that you have to aim where the star will be rather than where it is. Aberration certainly works for *received* light, but not for transmitted or emitted light; to hit a moving target you have to adjust the angle of your emissions/transmissions, and it is this adjustment which actually causes aberration. Light at the receiving end comes from a different direction than the one you might expect because of this adjustment.
But this has intrigued me; so I’ll take Ron S’ advice and educate myself about the phenomenon.
I thought I had worked it out, but after Ron’s last post I’m confused again. For a moment it looked as if he could be right, but this brought up a new problem. Stellar rotation rates are comparable to proper motion – actually sometimes they are much larger > 100km/s. This means that – from the reference frame of Earth – the gas disc that flashed that light signal to us 4.26 years ago might well be stationary, or even moving in the opposite direction to the star. Ughh!
No? How so? Are you saying gravity has anything to do with this? Easy thought experiment: Make AC and Sol massless, but still moving the same way. Surely, then, light will travel in straight lines? Will you then have to aim ahead? And how can that be if your math does not include mass or gravity?
I am not buying it. The Wikipedia article about Relativistic beaming has nothing like your assertion in it, as far as I can tell. Perhaps you could point to a reference which explicitly supports your claim that aiming a light beam directly at a moving target will allow you to hit it.
Aberration, as the term is explained in the Wikipedia article, is actually not a phenomenon of relativity, it occurs in ordinary circumstances like rain. And we all know for sure that shooting ordinary moving targets with ordinary projectiles requires “aiming ahead”.
Rob, the equations as presented are for “inertial” frames. Therefore not for a rotating star. In this discussion we simplified quite a bit by restricting ourselves to purely transverse motion for inertial frames, which is only a momentary thing for inertial frames comoving with their respective stars. To add in the affects of acceleration, radial motion, changes in those quantities over time and, yes, even gravitation, you’ll have to delve deeper.
No, I think that I have proof that aberration must be in the other direction without getting lost in calculation. Think of Earth as a starship freefloating in space. Now accelerate it in a constant direction, say originally 45deg from Alpha Cen, to relativistic velocities. Due to lengthwise contraction, as gamma increases we will OBSERVE the star move closer and closer to 90deg from our path, but due to aberration we will SEE it moving closer and to zero degrees from us. Now if we send out a message to AC’s observed position at any finite velocity, we will always find that AC has moved BEHIND this from our reference frame by the time it arrives. Therefore we must send out this message even further behind this line, even though we view it well in front of it.
Rob: “No, I think that I have proof that aberration must be in the other direction without getting lost in calculation.”
(sigh…) You have a proof without doing a calculation? Oh, right, sure you do.
To both you and Eniac, you don’t have to believe me and I am not obliged to convince you. I gave the elements of my reasoning in earlier posts, I did one actual calculation and even pointed to one (of many) excellent texts on the subject (did you notice that, Eniac?). That’s enough of my time. The rest is up to you.
There is something else that’s puzzling me about any equations that you are looking up Ron. Astronomers never care about the true position of stars being off due to that star’s proper motion. On the other hand they care desperately about aberration induced change in visual positions due to the Earth’s change in relative motion. Why would their texts give a highlighted equation for the former, when it could easily get confused for the latter, but would be in the opposite direction?
Ron: Don’t you mean arctan(v/c), instead of c/v?
Eniac, when Ron said “In any case, no observer will “see a photon going in a straight line”.” wasn’t he just being pedantic about the difference between seeing and observing? He certainly never mentioned general relativity.
Ron S: If AC is stationary, and we are moving to the right, then, due to aberration, the light from AC will appear to us as coming slightly from the right of the actual direction it is going. If we send light in that direction, our motion will add an additional aberration, again to the right. Your formula on aberration is correct, but you have misinterpreted the signs. The two aberrations do not cancel, they add up.
You mention the Wikipedia article, which comes up completely empty on this subject, and a text (D’Inverno) which may be a fine book, but without a quote I do not know that it actually addresses the specific subject we talk about, or just the phenomenon of aberration, which you then proceeded to misinterpret the signs of. I will certainly not go to a library and search an entire book just to find out what I am already quite sure of: That you are wrong.
Your “go look it up, I don’t have time to bother with this” attitude and aloof certainty in being correct strike me as disingenuous and are not helping the discussion.
Eniac says “And we all know for sure that shooting ordinary moving targets with ordinary projectiles requires “aiming ahead”.”
Yes we do, and we also all know that the faster that projectile the smaller that correction. Ron’s claim is simply that at c this effect is exactly zero. I am also sure that the magnitude of the effect is just right for his claim. The only point at which Ron and I differ is in the direction of that aberration wrt that needed for the “projectile”.
Ron thinks that the direction is forward of AC’ s true position, I which case an observer on AC would see a disproportionate surface of our forward side, unlike other aberration affected observers, that see a disproportionate surface of an objects backside.
I think I’ve found Ron S’ mistake; I’ll get it checked out at Bad Astronomy and get back to you.
(a clue; if I’m right, his calculations are quite correct).
Eniac, it is very dangerous to ascribe motive to others. Experts in general relativity tend to be comfortable with results that they can only understand in calculation, and that makes these sort of discussions difficult for them. We are trying to solve this with aid of diagrammatic representation, and I suspect Ron is not.
Rob:
It is not, though, as the formula clearly shows. For arctan(c/v) to be exactly Pi (no aberration), c needs to be at infinity. For this to be otherwise, there would have to be a formula that contains both the projectile velocity vp and the relativity constant c, in which the aberration goes to zero as vp approaches c. No such formula has been given, and I do not think there is one.
Rather, I understood Ron as saying that there are two aberrations that cancel, which, if I am not mistaken, would lead us to the nonsensical conclusion that you do not have to aim ahead at any projectile velocity.
While I agree with you that it is dangerous to ascribe motive to others, I do think you hit the nail on the head. There is a temptation to generalize “common sense is sometimes misleading”, to “common sense is always misleading”. Probably not limited to experts in relativity, but particularly understandable in them.
Isn’t it ironic, then, that the very foundation of relativity, it’s origin, lies in Einstein’s Gedanken-experiments trying to reconcile the constancy of the speed of light with the relativity principle. The math was secondary, the “common sense” reasoning was first. Although, of course, in the later development of general relativity, the math bloomed to such dizzying heights that what you say is absolutely true, now.
Eniac, whether we are on AC or Earth there would be only one aberration. Only a third reference frame will calculate that there are two. So we have one aberration from the current true position, and one aiming correction to hit a moving target.
However I was deadly serious about why astronomers would want an equation that finds true position due to stellar motion, rather than corrections needed due to variation in velocity of the Earth and its surface. I struggle to think of a practical usage for the former. If it is for METI then Ron’s claim makes that irrelevant, but what else could it be for? Any ideas here would be greatly appreciated.
Anyhow I believe that I have gleaned the following of interest from the discussion: high resolution imaging of two rapidly rotating stars in close orbit would have to be adjusted for aberration.
Great comments about commonsense. It can be very dangerous and hold us back, as mathematics was by Zeno’s paradox, but let’s not abandon it altogether.
It took me some time and several thought experiments to find out the problem; it seems that, although the light-time correction and the aberration are ‘equal and opposite’ they do not cancel each other out, but instead they are just different ways of looking at the same thing (in this context anyway).
The thread at Cosmoquest/Bad Astronomy in which I worked through to this realisation (with several diagrams) is here
http://cosmoquest.org/forum/showthread.php/141875-The-Aberration-of-light-and-sending-a-message-to-Alpha-Centauri
if there are any errors in that chain of reasoning please let me know.
What’s the conclusion here?
To my understanding, any communication beam would have to adjust for light speed delay and relative motion. You would aim the beam somewhere off-center of the visual target, unless the numbers happened to line up perfectly (that is, if the adjusted target falls where the visual is)
The only way it would make sense to aim at the visual target is if c were infinitely fast, which it isn’t.
xcalibur: Yes, you are correct, this is the conclusion. It seems, though, we were unfortunately not able to get Ron to agree with it, so I suppose it isn’t quite final.