Figuring out how fast a star spins can be a tricky proposition. It’s fairly simple if you’re close by, of course — in our Solar System, we can observe sunspot patterns on our own star and watch as they make a full rotation, the spin becoming obvious. From such observations we learn that how fast the Sun spins depends on where you look. At the equator, the rotation period is 24.47 days, but this rotation rate decreases as you move toward the poles. Differential rotation means that some regions near the Sun’s poles can take as much as 38 days to make a rotation.
Because of these issues, astronomers have chosen an area about 26 degrees from the equator, where large numbers of sunspots tend to appear, as the point of reference, giving us a rotation of 25.38 days. You can imagine how complicated solar rotation gets once we look at other stars. We can’t resolve them to begin with, much less their ‘starspots,’ but what we can do is measure the decrease in light that starspots cause as they rotate around the star. You can see why studying a lightcurve like this resembles searching for transiting exoplanets, and in fact a mission like Kepler has to take the possibility of false positives from starspots into account.
Determining the Age of a Star
Stars between 80 and 140 percent of the Sun’s mass are the subject of new work on stellar spin by Søren Meibom (Harvard-Smithsonian Center for Astrophysics) and team. Using Kepler data, the researchers homed in on a 2.5 billion year old cluster called NGC 6819, part of a continuing investigation of stellar spin rates. Meibom’s work is part of the broader Kepler Cluster Study, for which he is the principal investigator. The work uses data from the original Kepler mission, the four years of data before the current K2 mission, to study star clusters.
The goal is to develop a precise method of obtaining the ages of stars like these, a method co-author Sydney Barnes (Leibniz Institute for Astrophysics) calls ‘gyrochronology.’ Stellar spin is the critical factor because stars slow down as they age, while other indicators, like size, temperature, and brightness, stay relatively constant. So far we’ve been able to use spin rate to determine stellar ages only with fast-spinning stars in young clusters. Starspot activity is prominent on young stars and thus easier to detect. We’re also helped by the fact that the pattern of color and brightness in a cluster can give us a good read on the overall cluster’s age.
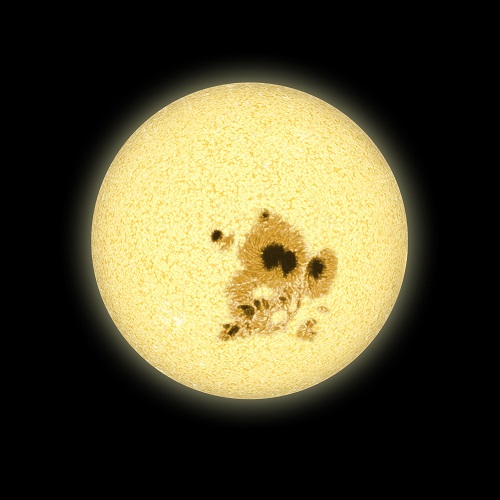
Image: It’s easier to tell the age of a young star because they rotate more quickly and have larger starspots. Credit: David A. Aguilar (CfA).
Thus we can correlate spin rate with age in specific instances. Get beyond about 600 million years in stellar age, though, and there is a huge gap between these young stars and stars as old as our 4.6 billion year old Sun. How fast do stars of intermediate ages spin? In this video on his work, Meibom refers to the ‘four billion year gap’ created.by our inability to measure spin for older stars. Young, rapidly spinning stars with large starspot regions, where brightness changes are pronounced, show a far more marked lightcurve than older stars, where starspot activity has dropped and teasing out the spin rate takes us to the limit of our instruments’ capabilities.
The Kepler telescope’s exquisitely sensitive measurements of stellar brightness are what has allowed us to fill in the gap. Studies of the cluster NGC 6811 produced the first measurements for the spin rate of one billion year old stars in 2011. Analyzing NGC 6819 data, Meibom and team have now been able to measure spin rates for 30 2.5 billion year old stars. We can thus plot spin against age on a far more meaningful graph, allowing us to extrapolate that when the Sun was 2.5 billion years old, its spin rate was roughly 18 days, with the rate dropping to eleven days when the Sun was 1 billion years old. A stellar ‘clock’ like this can help us determine which stars have planets that have had time for complex life to evolve. Looking forward, studying planets like our own around much older stars will give us clues to what lies ahead for the Earth.
“Now we can derive precise ages for large numbers of cool field stars in our Galaxy by measuring their spin periods,” says Meibom. “This is an important new tool for astronomers studying the evolution of stars and their companions, and one that can help identify planets old enough for complex life to have evolved.”
The paper is Meibom et al., “A spin-down clock for cool stars from observations of a 2.5-billion-year-old cluster,” published online in Nature 5 January 2015 (abstract). Links to the full text, and to video of the AAS press conference where these findings were announced, are available along with much more material on stellar age here. A CfA news release is also available.



Great, pure science by Meibom Et, all.
In addition to creating a methodology for determining the age of star
there is another quite important benefit:
In the future when colonization targets are being analyzed, we can
eliminate targets where the Primary star is too close to exhausting it’s
H2 fuel. We can watch out for the other hazard of a star that is too young and is emitting powerful flares as they are wont to.
On that note, one would like to include as many G,K, stars in a survey of
possible Colonization targets. But I think If I had my choice I would choose
a K star with total of 20 Billion year main seq lifespan, and the star should be in only it’s 5th billion year of age. The question is, at that age is it too prone
to flaring.
Would it be possible to determine spin by Doppler shift? I envisage measuring the width of a smeared band that indicates the + & – velocity of each limb. It would no doubt have to be very precise and is not likely to be as accurate as star spots, but it would be universally applicable to any star rotating approximately in our plane.
Alex, I can think of a couple of potential problems. One is limb darkening. Some compensation for should be possible though without knowing the “atmosphere” thickness it could underestimate the rotation rate. The second is the attitude of the rotation axis. A measure of Doppler spreading could only be a minimum value. So, I would guess it could be useful if the objective is to measure any particular star’s rotation. For this study’s purpose it’d be less useful than a statistical sampling of stars with a persistent surface feature.
@Alex,
Spectra has long been used to determine rotation rates of stars; here’s an article from 1929 that even mentions previous work (Shajn, G.; Struve, O. “On the rotation of the stars”: http://adsabs.harvard.edu/abs/1929MNRAS..89..222S)
…and even trace star spots ( Vogt, Steven S.; Penrod, G. Donald; Hatzes, Artie P. “Doppler images of rotating stars using maximum entropy image reconstruction” : http://adsabs.harvard.edu/abs/1987ApJ…321..496V)
While this paper is certainly interesting since it used a large sample of stars, there may be a bit too much PR spin on it.
Spin is determined by Doppler spectroscopy. The faster it spins the more one side moves away, increasing the wavelength , so called “red shift” . The opposite occurs on the other side with consequent shortening or “blue shift”. The degree to which these occur helps determine spin speed. The complicating factor is “differential rotation” in that different latitudes of a star rotate at different rates, with the equatorial region the fastest. The figures you see quoted represent the average of all these different rates. All of this comes under the field of Asteroseismology which is almost the spectral representation of a star’s acoustics and is critical to determining what goes on inside stars from looking at oscillations arising from the depths in the surface spectra. Complicated but now very refined .
As a related point in stars like the sun and this article, this differential rotation continues to the bottom of the do called “convergent zone” of the star, about 70% out from the centre and after that the remainder of the star acts like a solid body and rotates at the same rate. The “spin down” over time described in the article is caused by “magnetic breaking” whereby the stars magnetic flux lines interact with its solar wind to act as a brake over time.
Problems occur in active stars whose spectra are more difficult to interpret . Most M and some K stars could fall into this class, genuinely later ones though. Very fast rotators like OBA and some F stars cause problems too as their spectral lines are forced together by the rapid spin again ,asking them difficult to interpret.
Alex and FrankH point out that there are other, more conventional methods for determining spin. I believe, also, that age can be estimated fairly well from a star’s location in the Hertzsprung-Russel diagram, so I have to agree that some of what we read here may be “spun” a just a little too much ….
Very interesting, nevertheless.
Sorry if this is a repeat question, but with the thousands of exoplanets now discovered; Safe to say Zero correlation between spin rate and probability of having planets? I.e., slow spin equals higher chance? A dead hypothesis?
This is an important paper and in fact a fine-tuning of the already known methodology of gyrochronology, by Barnes et al.
The paper actually mentions 85% of solar mass as the minimum.
A few things disappoint me a bit, that is to say, to make it even better I would have liked this paper to have included:
– Stars with somewhat smaller masses. 0.85 * solar corresponds to about 0.6 * solar luminosity, it would be so useful to be able to go down, for solar type stars, to about 0.2 * solar lum.
– The most important and summarizing feature in the paper is Fig. 1, The schematic P–t–M surface, which shows the 3-dimensional relationship between rotation period, Mass (derived from B-V value) and age. However, this figure, though very elegant, does not read individual data points very well. So it would have been useful to have a summarizing graph showing the Age – Rotation relationship for various masses (i.e. multiple lines in a 2-dimensional graph).
– Further to my previous point: it should now be possible to come up with a rather simple formula to calculate the age of a star, by filling in its mass and rotational period. I am missing this formula, unless the one in Methods 3, i.e. t = (T/kc)ln(P/P0) + (ki/2T)(P^2 – P0^2) is meant. It is not qu9te cleat to me what should be filled in for T (it is a B-V to mass conversion?).
Furthermore, what is interesting to note, is that the authors mention in Methods 5 (Are tidal interactions with close companions a concern for gyrochronology?), that this gyrochronology method cannot be used for very close binary stars (less than 0.2 AU apart), and not reliably for stars with hot Jupiters (orbit less than 10 days, which are a very small minority anyway). For other binaries and planetary companions there is no significant influence, because tidal interaction scales as the inverse of the binary semi-major axis to the 6th (!) power.
Following on from my remarks yesterday in relation to judging rotation from active stars, particularly M dwarfs , there is a related article in arxiv today by Robertson et al showing how Stellar activity can interfere with the constraint of planets , in this case GJ176. This is an unusual star in that despite being old with a slow spin, it us one of the most active M stars. So there are exceptions to everything and limitations to discovery techniques too. The key is resonance. That said , rotation rate is critical in turn for excluding “false positive” planetary signals , as illustrated by GJ 176. Despite having a planet with a 9 day period, various other signals have been detected but they are all in resonance with the star’s rotation. They are likely to be surface activity coming in and out of line of sight, sunspots for instance , rather than planets.
“when the Sun was 2.5 billion years old, its spin rate was roughly 18 days, with the rate dropping to eleven days when the Sun was 1 billion years giving us”. ” a rotation of 25.38 days. . ”
Funny star, Sol.