The Titius-Bode law has always been a curiosity, one often attributed to little more than happenstance. But recently this numerological curiosity, which predicts that planets in a solar system appear with a certain ratio between their orbital periods, has been the subject of renewed investigation. Francois Graner (Ecole Normale Superieure, Paris) and Berengere Dubrulle (Observatoire Midi Pyrenees, Toulouse) revisited Titius-Bode in the 1990s, asking whether it actually flagged symmetry properties that most solar systems should exhibit.
And now continuing work out of Australian National University and the University of Copenhagen has made predictions using a modified version of the law that can be tested against observation of known exoplanetary systems. So we need to refresh our memory on the formulation, which shows us a relationship that predicts planetary orbits. Take a sequence where each number is double the number that preceded it. Thus 0, 3, 6, 12 and so on. Add 4 to each of these numbers, then divide the result by 10. If you examine our Solar System in terms of astronomical units (AU), the planets follow the sequence in many respects.
Enough so, at least, that the lack of a planet in what we now call the main asteroid belt led Johann Bode to suggest that a planet should appear at 2.8 AU between Mars and Jupiter, where the dwarf planet Ceres was subsequently found. The Titius-Bode formulation, developed in the 18th Century by Johann Titius and later discussed by Johann Elert Bode, had also received a boost in 1781 when the outer system planet it predicted at 19.6 AU was discovered at 19.2 AU (Uranus). Neptune, however, turned out to be 30.1 AU out instead of the Titius-Bode prediction of 38.8, while Pluto was found at 40 AU instead of 77.2.
Can some form of the Titius-Bode formulation still be useful to us in exoplanet work? Steffen Kjær Jacobsen (Niels Bohr Institute, Copenhagen) and fellow researchers Charles Lineweaver and Timothy Bovaird (the latter both at ANU) wondered whether a modified form of Titius-Bode might be of use in predicting exoplanet orbits. Developing work first presented in a 2013 paper on the subject, the authors believe the results can be applied to existing data. Says Jacobsen:
“We decided to use this method to calculate the potential planetary positions in 151 planetary systems, where the Kepler satellite had found between 3 and 6 planets. In 124 of the planetary systems, the Titius-Bode law fit with the position of the planets as good as or better than our own solar system. Using T-B’s law we tried to predict where there could be more planets further out in the planetary systems. But we only made calculations for planets where there is a good chance that you can see them with the Kepler satellite.”
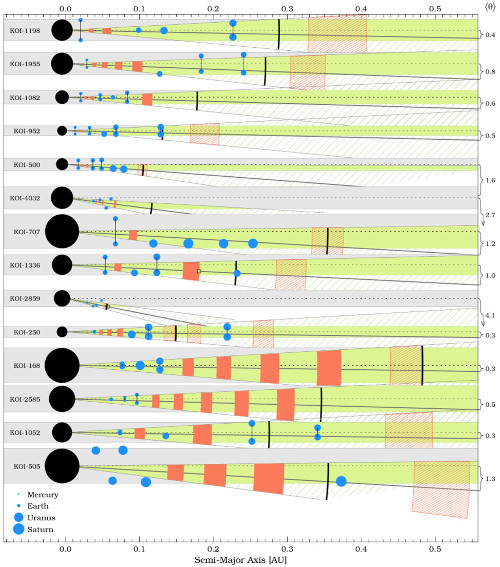
Image: Exoplanetary systems where the previously known planets are marked with blue dots, while the red dots show the planets predicted by the Titius-Bode law on the composition of planetary systems. 124 planetary systems in the survey – based on data from the Kepler satellite, fit with this formula. Credit: Timothy Bovaird et al., 2015.
In their paper in Monthly Notices of the Royal Astronomical Society, the team explains that they took the 27 planetary systems that did not fit the Titius-Bode requirements and added planets where Titius-Bode predicted they would be located. By adding planets between the already known planets, their work predicted a total of 228 planets in the 151 planetary systems. From this the team produced a priority list of 77 planets in 40 systems.
These are planets the researchers suggest should be searched for in the Kepler data, a chance to falsify the Titius-Bode predictions drawing on existing datasets. This work follows up co-authors Lineweaver and Bovaird’s previous investigation of Titius-Bode possibilities in exoplanets, which predicted in 2013 the existence of 141 new exoplanets in 68 systems. The following year Changcheng Huang and Gaspar Bakos performed a search of Kepler data for 97 of the planets thus predicted, resulting in the confirmation of five of them. The current paper tunes up the 2013 paper’s methodology, as discussed within:
In this paper, we perform an improved TB [Titius-Bode] analysis on a larger sample of Kepler multiple-planet systems to make new exoplanet orbital period predictions. We use the expected coplanarity of multiple-planet systems to estimate the most likely inclination of the invariable plane of each system. We then prioritize our original and new TB-based predictions according to their geometric probability of transiting. Comparison of our original predictions with the HB14 [the Huang/Bakos paper] confirmations shows that restricting our predictions to those with a high geometric probability to transit should increase the detection rate by a factor of ?3.
If the Titius-Bode predictions were to hold up, from 1 to 3 habitable-zone planets should exist in each of the systems. The team ran an additional study of the 31 systems out of the 151 studied where planets have been found close to the habitable zone, finding there should be an average of two planets in the habitable zone. If the implications of Titius-Bode are broadly true, then the potential exists for billions of stars with planets in the habitable zone throughout the galaxy, a finding that subsequent analysis of Kepler data and future work may support.
The paper is Bovaird, Lineweaver and Jacobsen, “Using the inclinations of Kepler systems to prioritize new Titius–Bode-based exoplanet predictions,” Monthly Notices of the Royal Astronomical Society Vol. 448, Issue 4, pp. 3608-3627 (abstract). The 2013 paper is Bovaird and Lineweaver, “Exoplanet predictions based on the generalized Titius–Bode relation,” MNRAS Vol. 435, Issue 2, pp. 1126-1138 (abstract). The Huang/Bakos paper is “Testing the Titius–Bode law predictions for Kepler multiplanet systems,” MNRAS Vol. 442, Issue 1, pp. 674-681 (abstract).



I would be VERY cautious of relying on the dubious predictions of the Titus-Bode “law” applied to extrasolar planetary systems. There are professional, peer-reviewed astronomy and planetary science journals that have explicit editorial policies banning the publication of any papers dealing with the T-B law because it smacks of numerology (obviously MNRAS is not one of them). Until a sound theoretical model that accurately explains the observed spacing of planets in various systems is formulated and tested, rigorous statistical analyses of extrasolar planetary systems (e.g. what has been done with Kepler finds) are a much better means of predicting the numbers of potentially habitable planets than T-B mumbo jumbo.
Titius-Bode always looked like chaotic bifurcation to me. Bifurcation, bifurcation, bifurcation, chaos. Hard to tell what chaos in three dimensions looks like, since the next series of planets (and moons) is eccentric and some of the moons of Jupiter are retrograde. After all, the planets are not EXACTLY coplanar, the dwarf planets past Neptune definitely are not, and the retrograde moons are very eccentric.
Given that planets are postulated to have changed orbits, what does the T-B law (rule?) even mean? Does it have some implication for final, stable orbits?
What I would like to see is some statistical analysis of the T-B relation across the known systems. Is the relation better than chance?
Even aside from the T-B relationship being probably just random chance in our own system, surely if there’s one thing we’ve learned from the past couple of decades of exoplanet discoveries, it’s that the configuration of our own system is not typical or predictive of how other systems are configured. So this whole paper makes no sense to me.
Curious comments. Obviously ‘Bode’s Law’ is not a law. The ‘Titius-Bode formulation’ is an observation. One that was used to ‘predict’ the asteroid belt and Uranus. You all seem to forget that the n-body problem has no solution. This is not a limitation of nature. It is a limitation of the mathematical tools used to model gravity. Iterative solutions are good for small instances, but they cannot model the entire solar system.
If T-B is an approximation (obviously it is not exact) of something analogous to the gas laws, isn’t it worth investigating? Why the gas laws? Because ‘pressure’, ‘volume’ and ‘temperature’ are emergent properties of large numbers of atoms with mass, velocity and direction.
I have heard T-B described as maybe some kind of ‘resonance’, but it seems to be an ‘anti-resonance’, since there are clear areas of the asteroid belt that fall in Jupiter’s resonances. I hadn’t heard that T-B was not allowed in journals. This seems both short sighted and narrow minded. Not that T-B papers shouldn’t be peer reviewed for scientific accuracy, but T-B works in limited cases. Numerology? Not a chance.
Kind of like the U. S. Patent Office not allowing cold fusion patents. Oh, wait, muon catalyzed fusion is demonstrated and confirmed. And cold. But fusion is probably totally useless too.
Agree with the first 4 commenters. Titius-Bode analysis has less validity than string theory (sic), and that says it all. If, as Andrew has suggested, there ever is a convincing demonstration that this mathematical oddity has some physical basis or predictive value, I would revise my opinion.
I had to double-check it wasn’t April first. This is the equivalent of a physic
prediction. When it accidentally gets one or two guesses right we’ll hear all about it. If it’s a total miss everyone shrugs. In the former we’ll get one or more papers like Alex Tolley suggested, but still read about it on certain sites for the next hundred years.
Seems to me that near-resonances are more of a thing in terms of system architecture than Titius-Bode is, at least in some systems. On the other hand, planet prediction is a dangerous game! Take the example of HD 74156 d, announced as a successful prediction of the packed planetary systems hypothesis, which ended up not surviving follow-up analysis – and the packed planetary systems hypothesis had a far stronger theoretical basis than the Titius-Bode relationship.
andy’s point seems extremely well taken to me. As we continue our exoplanet investigations, their brief history seems to shout out that the most carefully crafted predictions quickly run aground!
When I took an astronomy course, the Titius-Bode law was intriguing to me. A big part of science is finding patterns in how things work, and it’s a compelling pattern. It made sense to me that it predicted Ceres, because the Asteroid Belt is where a planet would have formed if it hadn’t been broken up (presumably by Jupiter’s gravity). It’s also interesting that Pluto was found so close to Neptune’s predicted value.
I realize that many in science don’t take it seriously, but it’s hard to dismiss such a strong set of coincidences. It seems to me that Titius-Bode reflects some kind of gravitational resonance that took hold when planets were forming out of the protoplanetary disk, and that this resonance breaks down after a certain distance from the sun.
As an alternative to looking for our solar system’s Titius-Bode pattern in other systems, we should consider that other systems may have a different pattern of resonances. The presence of hot jupiters and brown dwarves may also disrupt the pattern.
xcaliber, I still think that ‘resonance’ is the wrong word for the T-B series. It seems more like stable orbits where planetary resonances do not effect each other, and the spaces between the planets are the resonances; like the Kirkwood gaps in the main asteroid belt caused by Jupiter. Closer to Jupiter than a 2:1 resonance, the asteroid belt is swept pretty clean.
Remember that Neptune and Pluto are locked in a 2:3 resonance, and 90482 Orcus is an exact opposite orbit of Pluto. By the time you get this far, T-B seems to break down entirely. T-B also does not work to describe the Galilean moons of Jupiter, since three are locked in a Laplace resonance.
This just in, related and very interesting: another step in the modelling of planetary systems:
Jupiter’s decisive role in the inner Solar System’s early evolution;
http://www.sciencedaily.com/releases/2015/03/150323162245.htm
http://www.pnas.org/content/early/2015/03/18/1423252112
I think this is accurate.
As for Titius-Bode breaking down at a distance, and the Galilean moons, this is explained by my idea – which is that the T-B pattern is rooted in the protoplanetary disk and planetary formation. Naturally the Galilean moons wouldn’t be affected, and if the Sun’s gravity plays an important role, then the distance breakdown would also make sense.