The advantages of neutral particle beam propulsion seem clear: Whereas a laser’s photon beams can exchange momentum with the sail, neutral particle beams transfer energy and are considerably more efficient. In fact, as we saw in the first part of this essay, that efficiency can approach 100 percent. A mission concept emerges, one that reaches a nearby star in a matter of decades. But what about the particle beam generators themselves, and the hard engineering issues that demand solution? For that matter, how does the concept compare with Breakthrough Starshot? Read on as James Benford, working in collaboration with Alan Mole, describes the salient issues involved in building an interstellar infrastructure.
By James Benford and Alan Mole
We discuss the concept for a 1 kg probe that can be sent to a nearby star in about seventy years using neutral beam propulsion and a magnetic sail. We describe key elements of neutral particle beam generators, their engineering issues, cost structure and practical realities. Comparison with the Starshot laser beam-driven concept gives roughly similar costs.
Beam Generator Concept
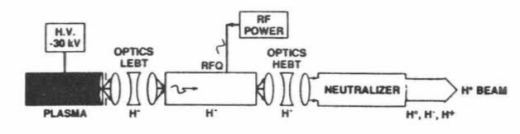
Figure 1 Block diagram of early neutral particle beam generator [1]. Drift-Tube Linac is not shown.
Creation of the neutral particle beam begins with
1. Extraction of a negative ion beam (negative ion with attached electrons) from a plasma source; it then drifts into the first acceleration stage, the RFQ. The first element of the accelerator will appear much like the geometry shown in figure 2. Here ions are extracted from the plasma source on the left by electrostatics and brought by a converging magnetic field to the linear accelerator.
Figure 2. Ion beam on left is propagated along converging magnetic field to the linac.
2. The ion beam enters a radiofrequency quadrupole (RFQ) accelerator, a vane-like structure where the application of radiofrequency power produces a continuous gentle acceleration much like a surfer riding a wave. It also provides strong electrostatic focusing to prevent divergence growth. The structure bunches the particles in phase space.
The RFQ fulfils at the same time three different functions:
- focusing of the particle beam by an electric quadrupole field, particularly valuable at low energy where space charge forces are strong and conventional magnetic quadrupoles are less effective;
- adiabatic bunching of the beam: starting from the continuous beam produced by the source it creates with minimum beam loss the bunches at the basic RF frequency that are required for acceleration in the subsequent structures;
- acceleration of the beam from the extraction energy of the source to the minimum required for injection into the following linac structure.
3. After the ions exit the RFQ at energies of a few MeV, further acceleration to increase the particle energy is done with a drift-tube linac (DTL), which consists of drift tubes separated by acceleration regions, as shown in Figure 3. Particles arriving at the gaps at the proper phase in the radiofrequency waves are given acceleration impulses. When the electric field of the wave reverses, the particles are shielded from being accelerated by passing through the drift tubes. The typical accelerating gradient is a few MeV/m.

Figure 3. Drift-Tube Linac, which consists of drift tubes separated by acceleration regions.
4. In order to maintain low emittance and produce the microradian divergence we desire, the beam is expanded considerably as it exits the accelerator. Beam handling elements must have minimal chromatic and spherical aberrations.
5. Beam pointing to be done by bending magnets with large apertures.
6. Finally, the extra electrons are stripped from the beam, making a neutral particle beam. This can be done with by stripping the electrons in a gas neutralization cell or by photodetachment with a laser beam. It may be possible to achieve 100% neutralization by a combination of methods. Thus far this high-efficiency neutralization has not been demonstrated.
Beamer Engineering
There are several possible schemes for building the beam generator. Both electrostatic and electromagnetic accelerators have been developed to produce high power beams. The most likely approach is to use linear accelerators. In the past, the cost of an electromagnetic accelerator is on the order of a person year per meter of accelerator (~1 man-year/m) but this could be larger for the more sophisticated technologies.
The power system to drive such accelerators could come from nuclear power (fission or fusion) or solar power. Furthermore, if it were to be space-based, the heavy mass of the TW-level high average power required would mean a substantially massive system in orbit. Therefore Mole’s suggestion, that the neutral beam be sited on Earth, has its attractions. There is also the question of the effects of propagating in the atmosphere, on both beam attenuation and on divergence.
If the beam generator were to be on Earth, it should all be at the highest altitude for practical operations. The Atacama Desert, for example, would offer very low humidity and half of sea level pressure. In addition, a way to reduce beam losses in the atmosphere would be to launch a hole-boring laser beam in advance just before the neutral beam. This laser would heat up a cylinder of atmosphere to lower the pressure, allowing the neutral beam to propagate with less loss. Such hole-boring exercises have been conducted in laser weapon studies and does appear to be a viable technique.
The final neutral beam can be generated by many small beam drivers or a single large beam driver. If a great number of driver devices and their associated power supplies are required, increasing the construction and maintenance expense of this portion. Of course, economies of scale will reduce the cost of individual segments of the Beamer by mass production of the system modules. Making such choices is an exercise for future engineers and designers.
Neutral particle beam generators so far have been operated in pulsed mode of at most a microsecond with pulse power equipment at high voltage. Going to continuous beams, which would be necessary for the seconds of beam operation that are required as a minimum for useful missions, would require rethinking the construction and operation of the generator. The average power requirement is quite high, and any adequate cost estimate would have to include substantial prime power and pulsed power (voltage multiplication) equipment, the major cost element in the system. Of course, it will vastly exceed the cost of the Magsails, which is an economic advantage of beamed propulsion.
However, this needs economic analysis to see what the cost optimum would actually be. Such analysis would take into account the economies of scale of a large system as well as the cost to launch into space versus the advantages of beaming from Earth.
Beamer Cost Estimates
The interstellar neutral particle beam system described here is a substantial extrapolation beyond the present state-of-the-art. Nevertheless, estimates can be made of both the capital and operating costs.
The cost of the Beamer is divided between the cost of the accelerator structure (RFQ and DTL) and the power system that drives it. For a cost estimate for the Mercury system, we assume that the present day accelerating gradient is maintained for this very high-power system. That gradient is ~ 2 MeV/m. For the mercury neutral particle beam the length of the 1.35 GeV accelerator would be 675 m.
There is an extensive technology base for drift-tube linacs; there are many in operation around the world [2]. We use as a model the well-documented 200 MeV Brooklyn National Laboratory 200 MeV ion beam system, which was completed in 1978 at a cost of $47M. It used 22 MW of radiofrequency power and was 145m long. In that era, the cost of microwave equipment was ~$1/W. The cost today is ~$3/W, so the 22 MW would cost 22 M$ then and 66 M$ today. Since the total cost of accelerator was $47 M$, the Accelerator structure would cost 47 M$ -22 M$ = $25 M$. Thus at this level the two cost elements are roughly equal. The accelerator structure then costs $25 M$/145 m = $0.17 M$ per meter in 1978. We multiply all costs by a factor of three to account for inflation to get today’s costs.
To estimate the capital cost of the mercury in NPB described here, we have the following relations:
Caccl= 0.5 M$/m x 675 m = 350 M$
Cmicrowave= 3$/W x 18 TW = 5.47 B$
Therefore the dominant cost element would be the microwave system driving the accelerator.
However, high-volume manufacturing will drive costs down. Such economies of scale are accounted for by the learning curve, the decrease in unit cost of hardware with increasing production. This is expressed as the cost reduction for each doubling of the number of units, the learning curve factor f. This factor typically varies with differing fractions of labor and automation, 0.7 < f < 1, the latter value being total automation.
It is well documented that microwave sources have an 85% learning curve, f = 0.85 based on large-scale production of antennas, magnetrons, klystrons, etc [3]. Today’s cost is about $3/W for ~1 MW systems. Note that this includes not only the microwave generating tube, but also the power system to drive that continuous power. The 18 TW power needed would require 18 million such units. Therefore the cost is ~1.1 B$. Adding together the accelerator and microwave power system, the cost will be 1.45 B$.
The electrical power to drive this large system cannot possibly come from the electrical grid of Earth. Therefore a large cost element will be the system that stores the 162 TJ of energy. (Note that the beam power starts at zero and rises with time (t2) to 18 TW at the end.) From Parkin’s estimates of the Starshot energy storage system [10], based on Li-ion batteries, we take the storage cost to be $50 per kilowatt-hour, which is $13,900 $/TJ. Consequently the cost for the energy store is ($13,900 $/TJ) 162 TJ = 2.25 B$. So the energy stores cost is comparable to that of the accelerator.
The total capital cost is
Caccl= 350 M$
Cmicrowave = 1.1 B$
Cstore= 2.25 B$
Total accelerator capital cost is 3.7 B$.
The operating cost to launch a single Magsail is of course far smaller. It is simply the cost of the spacecraft and the energy to launch it. We will assume that the cost of the spacecraft will be on the order of $10 million. The cost of the electricity at the current rate of $.10 per kilowatt-hour is $4.5 million.
Total operating cost for a single launch is ~15M$.
Comparison with Starshot
The neutral particle beam approach is conceptually similar to photon beams such as the laser-driven Starshot project. A disadvantage of reflecting photons from the sail will be that they carry away much of the energy because they exchange only momentum with the sail. Neutral particle beams transfer energy, which is much more efficient. The reflecting particles may in principle be left on moving in space after reflection and thus the efficient energy efficiency can approach 100%.
The Starshot system, a laser beam-driven 1 gram sail with the goal of reaching 0.2c, has been quantified in a detailed system model by Kevin Parkin [4]. Since both the high acceleration neutral particle beam described here and Starshot are both beam-driven high-velocity systems, we make the following comparison between their key parameters and cost elements:
Physical parameters and cost elements of beam-driven probes
| Mercury Neutral Particle Beam System | Starshot | |
|---|---|---|
| Sail mass | 1 kg | 1 g |
| Velocity | 0.06 c | 0.2 c |
| Beamer capital cost | 1.45 B$ | 4.9 B$ |
| Energy store cost | 2.25 B$ | 3.4 B$ |
| Total capital cost | 3.7 B$ | 8.3 B$ |
| Energy cost/launch | 4.5 M$ | 7 M$ |
| Kinetic energy | 1.6 1014 J | 1.8 1012 J |
| Kinetic energy/ capital cost | 43.2 kJ/$ | 0.2 kJ/$ |
Here we have summed the accelerator and microwave power system costs for the neutral Beamer and the laser and optics cost for Starshot. A major caveat is that Parkin’s estimates have realistic efficiencies of the systems of Starshot, but our costs assume unrealistically high efficiencies.
Although they differ in detail, the two concepts give the same order of magnitude cost. However, the kinetic energy in the NPB-driven probe is 90 times that of the Starshot probe. This shows the disadvantage of reflecting photons from the sail: they carry away much of the energy because they exchange only momentum with the sail. Neutral particle beams transfer energy, which is much more efficient. The kinetic energy/capital cost ratio is 200 times greater in the NPB case.
It is instructive that the high-energy requirement of interstellar probes drives the existence of a stand-alone storage system, which is a major element in the total cost of both systems. The similarity of costs for these rather different beam- driven systems gives us some confidence that these rough estimates in this paper are credible.
Neutral Particle Beam Realities
Practical realities are always bad news. Performance of most systems degrades to below their design points because of inefficiencies of processes. Note that the beam systems described here are perfectly efficient, as determined from equation 5. That is, the beam reflects from the sailcraft with perfect efficiency, so as to stop dead, transferring all the energy to the spacecraft. The realities of neutral particle beams in the present day are substantially poorer.
To see where the problems lie, we consider a daring experiment called BEAR, conducted 30 years ago [1, 5]. A neutral particle beam generator was actually deployed and operated in space and its performance was measured.
On July 13, 1989 the Beam Experiment Aboard Rocket (BEAR) linear accelerator was successfully launched and operated in space by Los Alamos National Laborotory. The rocket trajectory was sub-orbital, reaching altitude of 220 km. The flight demonstrated that a neutral hydrogen beam could be successfully propagated in an exoatmospheric environment. The cross-section of the rocket is shown in figure 4.
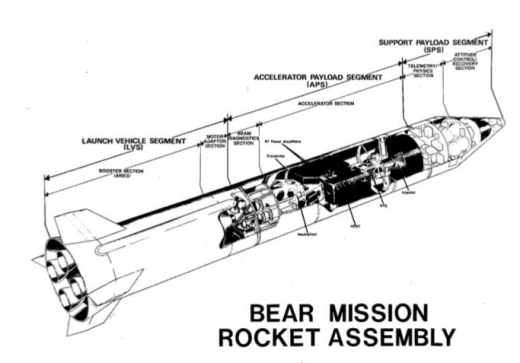
Figure 4. Beam Experiment Aboard Rocket (BEAR) [1].
The accelerator, which was the result of an extensive collaboration between Los Alamos National Laboratory and industrial partners, was designed to produce a 10 rnA, 1 MeV neutral hydrogen beam in 50 microsecond pulses at 5 Hz. The major components were a 30 kev H- injector a 1 MeV radio frequency quadrupole, two 425 MHz RF amplifiers, a gas cell neutralizer, beam optics, vacuum system and controls. The beam extracted was 1 cm in diameter with a beam divergence of 1 mradian. There was no unexpected behavior such as beam instability in space.
The design was strongly constrained by the need for a light- weight rugged system that would survive the rigors of launch and operate autonomously. The payload was parachuted back to Earth. Following the flight the accelerator was recovered and successfully operated again in the laboratory.
From the paper and report describing this experiment we see substantial inefficiencies, which should guide our future expectations.
The input power to the accelerator was 620 kW for 60 µs, a 7.2 J energy input. The beam as extracted was 27 mA at 1 MeV for 50 µs, which gives 1.35 J. The efficiency therefore is 19%, so approximately 4/5 of the energy supplied was lost in the beamline shown in figure 1. The major loss was in the neutralizer which was a xenon gas injected into the beamline. The efficiency of the neutralizer was changed by varying the amount of gas injected. They obtained 50% neutral hydrogen and 25% each of negative and positive hydrogen. Therefore the neutralization process was only 50% efficient in producing a neutral beam. This accounts for most of the loss. The other losses can be accounted for by inefficiencies in the optics of the low-energy beam region and the high-energy beam region.
In the 30 years since the flight, little work on particle beams has occurred at high power levels, because of the termination of the Strategic Defense Initiative. Doubtless substantial improvements can be made in the efficiency of NPB’s, given substantial research funding. Therefore the concept in this paper, with its hundred percent efficiency of energy transfer from the electrical system to the sail, is an upper bound on the performance. Consequently the parameters in Table 1 and the capital and operating cost estimates given here are lower bounds on what would actually occur.
Conclusions
The cost model presented here is lacking in realistic efficiencies. The next level of analysis should address this lack.
We can forsee a development path: a System starts with lower speed, lower mass Magsails for faster missions in the inner solar system. As the system grows, the neutral beam System grows and technology improves. Economies of scale lead to faster missions with larger payloads. As interplanetary commerce begins to develop, making commerce operate efficiently, outcompeting the long transit times of rockets between the planets and asteroids, the System evolves [6]. Nordley and Crowl describe such a development scenario [7]. We conclude that this concept is a promising method for interstellar travel.
References
1. P. G. Oshey, T. A. Butler, M. T. Lynch, K. F. McKenna, M. B. Pongratz, T. J. Zaugg, “A Linear Accelerator In Space-The Beam Experiment Aboard Rocket”, Proceedings of the Linear Accelerator Conference 1990.
2. H. B. Knowles, “Thirty-Five Years of Drift-Tube Linac Experience” Los Alamos Scientific Laboratory Report, LA-10138-MS, 1984. See also reference 4, pg. 81.
3. J. Benford, J. A. Swegle and E. Schamiloglu, High Power Microwaves, Third Edition, pg. 77, Taylor and Francis, Boca Raton, FL, (2015).
4. K. L. G. Parkin, “The Breakthrough Starshot System Model”, Acta Astronautica 152, 370-384, 2018.
5. G. J. Nutz, “Beam Experiments Aboard a Rocket (BEAR) Project Summary’, LA-11737, 1990.
6. J, Benford, “Beam-Driven Sails and Divergence of Neutral Particle Beams” JBIS 70, pg. 449-452, 2017.
7. G. Nordley and A. J. Crowl, “Mass Beam Propulsion, An Overview”, JBIS 68, pp. 153-166, 2015.



Hi Jim,
Very nice first pass design analysis. The parameters of the Mag-Sail payload will need some optimisation as will the best relative speed of the pusher beam. Rough estimates for the wire do give very high self-field at the skin of the wire, meaning the superconducting material will need to have very high critical current and will experience high hoop stress. Mike Minovitch’s glass reinforcing, from his magnetic scoop design from a few years ago, seems one option. One hopes that the quest for Room Temperature Superconductors might pay-off soon, making many components of this system more tractable.
$13,900 $/TJ is missing 3 0’s. Should be 13,900,000 $/TJ
Can someone explain why this system needs -ve ions, rather than +ve ones to work? Is there a technical or operational reason?
Easier to strip electrons after acceleration than to add them.
But ion engines use +ve Xe ions and inject the electrons. Is it the type of element that matters that determines the better approach?
You don’t necessarily need the ions & electrons in the ion engine exhaust to recombine since you aren’t trying to propagate a beam over long distances. You’re just trying to ensure your s/c doesn’t charge up. So, since its easier to strip an electron than add it, you strip the electron (or electrons) to make the ion, accelerate, then shoot the excess electrons out into the exhaust.
In an NPB, there’s no way I’m aware of to guarantee that relativistic electrons & +’ve ions would recombine before magnetic fields send them on their separate ways. (And even if you could, this would almost certainly add an uncontrolled element to beam divergence.)
Some immediate questions that come to mind:
While it looks attractive to place the beamer on the ground, what are the likely atmospheric losses even with a laser needed to “punch a hole” to improve performance? Starshot was considering a ground-based laser too. How do the 2 systems compare when their beams must traverse the atmosphere?
Is the DoD still pursuing particle beam weapons? If so, can this R&D be leveraged off? Or do you have a reverse problem, classification of this high-power particle beam array that cannot be allowed for civilian use? [Rather akin to the difficulty of acquiring nuclear bombs for Orion fanbois.]
If the efficiency drops to 10% for beam production and collector transfer, the capital costs escalate to $32bn, with a launch cost of $45m. Alternatively, the craft mass must be reduced to 100gm.
Some rough calcs suggest that the beam is going to fire for about 18 s, and the craft will be powered for about 160,000 km. If the beam is located on Earth, firing through the belt of satellites, can it even do this without damaging a satellite? (The same problem arises for the laser approach.) If the particle beam, power source, and power storage have to be parked in space, perhaps in cis-lunar space, what masses and costs are we now talking about?
In the previous essay, I asked about scaling down the system for pilot test purposes. If the beamer is on the ground, can a low power beam even penetrate the atmosphere at all, or must it be launched, much like the BEAR mission?
What impact on beam divergence and pointing accuracy is there from the Earth’s magnetic field? Is it insignificant?
One advantage of a ground-based NPB is that it cannot be deflected back to use as a weapon on ground targets, a possible objection to a similarly ground-based laser system.
In order to do R&D on an NPB propelled magsail probe, how does one proceed? Does testing of a complete sub-scale system need to be done in space, or can it be done on the ground with the sail in orbit? How much scale-down can be done to feasibility test a system for the lowest cost? How much testing can be done in vacuum chamber facilities? Can the magsail be tested with a substitute for teh beam to allow independent development, or must the NPB be ready for the magsail testing to go forward?
Seems Alex Tolley may have spotted a morass ahead. But that must be anticipated when basing exuberant speculation on modest technology. The proof of the pudding will be in the eating.
This system could only be really done in space.
The cost of any beam system that has to be put in space is going to be expensive, plus the possibility of weaponization will send every dictator into a frenzy and Russia and China will follow close behind.
The cost to develop a spacecraft that can be propelled by electron jets reaching 20,000 km/s or o.o66c during magnetic reconnection will be just the cost of the spacecraft!!!
This could not be weaponized and will be just considered a research project. Even starshot could not compete since the beam is already there in the Earth’s Magnetotail. The initial experiment could be done with a rideshare cubesat launch from a geosat mission so cost would be nominal!!! Let’s look at something that is feasible to at least get our foot in the door. Like they say Rome was not built in a day. ;->
https://centauri-dreams.org/2019/01/03/ultrahigh-acceleration-neutral-particle-beam-driven-sails/#comment-185234
I was wondering just how effective the ‘hole punching laser’ would be. The channel produced needs to have a residual atmospheric density equivalent to an altitude greater than 120 km or else the beam is going nowhere. (And to your later point, NPBs cannot reach the ground, for the same reason. The atmospheric density becomes a brick wall.)
To another of your points, the whole point of a *neutral* beam is that it is not bothered by Earth’s magnetic field.
If a truly neutral beam [i.e. neutral atoms/molecules and not a neutral plasma] is not affected by magnetic fields, then how would it interact with the craft’s magnetic fields?
Go back to Brett Bellmore’s point (first article) about induced ionization of a neutral bean in a magnetic field. Is the Earth’s magnetic field, albeit weaker, not going to have any similar effect? Siting the beamer on the mountain at the south pole would allow the beam to align with the Earth’s field, and not ionize. However, the aiming direction would be a bit limited… ;)
But note that the BEAM mission did not fully neutralize the ions, only 50% of them. Therefore some interaction with the non-neutral ions is going to occur, especially given that this proposed beam is not the short range of a weapon, but needs to reach the craft up to halfway to the Moon. Calculation and experiment will tell what impact the Earth’s field will have.
Details can matter. As an example, consider Lubin’s photonic drive where the laser light bounces back and forward between the laser and the craft’s mirror sail. Works in the lab over a short range. But in space, the craft would have to be perfectly perpendicular to the beam for this to work. Maybe a cubic reflector sail would ensure this, but given the difficulties of designing a basic sail that is stable in the uni-directional beam proposed by Starshot, I suspect not.
Any ions not successfully neutralized are lost to the beam. Near Earth, for example, I’d have to run the numbers multi-GeV Hg beams, but for H beams in the 10s-100s MeV, the stripping distances are 10s of km.
As far as interacting w/ the s/c magfields, I assume the authors have run the numbers & selected a magsail field (much greater than Earth’s intensity) which will ionize the NPB, else the entire operation would need to be far removed from our magnetosphere anyway.
I look at the cost for both and think bothbshould be pursued because they can be used for different types of exploration . Spend some money on a defense lobbyist.
I suspect a combination between a laser and particle beam would be better. I suppose we could use starshots reflective membranes with a hole in it and use a FEL with a reflective tube. The laser will bounce back and forth between the membrane and mirror near the FEL front accelerating the membrane at great force. The multiple energy transfers will greatly improve the momentum efficiency of the system. By charging the membrane and the tube walls to the same charge it will force a stability on the accelerated membrane. Free Electron Lasers can be very efficient.
By having a multi photon bounce the forces are multiplied considerably by up to 100 times meaning a much smaller machine. It can be configured to have no recoil as well.
http://www.deepspace.ucsb.edu/wp-content/uploads/2013/09/Interstellar-Flight-and-Recycling-Light.pdf
Surely the eventual location of a large NPB emitter or laser would be the far side of the moon? An earth based system just presents enormous problems in terms of the large numbers of satellites etc. in earth orbit. Yes, such a system on the moon would be enormously expensive but if NASA and others are going to continue to target the moon for various purposes including bases and a space station it seems obvious as a candidate location. One key element of course is reducing launch costs (cost of payload per launch) and NASA doesn’t seem to be taking that seriously at all with the proposed costs of SLS launches. SpaceX is clearly on the right track here obviously.
An understatement. Consider just the battery storage. A very optimistic specific energy is 1 MJ/kg. So 162 TJ is 162,000,000 kg.
Assume some super successful NewSpace rocket line company can deliver this for just $1000/kg to the lunar surface (excluding set up and maintenance). That is $162 bn, just for the batteries. The beamer, power supply, and any support facilities and crew rotation have to be added. So a lunar beamer is in the $10s tn just to start. For comparison, the whole Apollo program may have cost perhaps $200-250 bn in today’s money.
A lunar-based beamer is not going to happen unless we can drop costs by orders of magnitude from that very generous [fantastically optimistic?] figure I used. There is no justification for the cost involved.
I really like the idea of lobbing kg masses to the stars. In reality, this project can only work with either a ground-based beamer or some way to reduce energy demands with a space-based version. If the Plasma Magnet works at all, especially with this NPB approach, then this might be a better way to capture the beam energy as it would not require such a low diverging beam as the collection area could be much larger and expands as the particle density increases. This might make for a much simpler, lower-cost NPB. The approach could be tested for validity on the ground for quite a low cost.
The engineering and physics (speaking as a technical lay person) is beyond daunting. However Lithium batteries may not be the best choice for energy storage:
https://www.youtube.com/watch?v=Sddb0Khx0yA
I like the no nonsense style of the lecturer and he presents a convincing case of the economic superiority of liquid metal batteries for utility scale electrical energy storage. The cost per stored kWh was perhaps several orders of magnitude less than Lithium batters and there is virtually zero degradation of performance over thousands of charging cycles. The batteries, however, are quite heavy making them a dubious choice for space-based systems. However, the required elements may be relatively common on the lunar surface. If so, and with the extreme simplicity of the battery (just some refractories, certain salts and relatively pure aluminum and antimony) could make off-world production feasible. Admittedly, speculation piled on top of extrapolations but hey, that is sort of fun.
One advantage Breakthrough Starshot has is that the DoD is actively developing high power laser weapons. Lubin’s D-STAR 4 was pitched at vaporizing asteroids for planetary defense. (Whether actually ever used for that purpose, they can be sold to teh public for that purpose). What I don’t see is how a PBer can be sold as a plowshare, rather than a sword, and serious funding for R&D acquired.
With such grandiose projects, one needs to expend huge resources to end up with a single-use device – e.g. a starship. There rarely appears to be much thought on how to get there from more modest starting points. Dyson’s Orion or the BIS’s Daedalus/Icarus must assume a vastly larger economy to support those starships. That may never happen. They are also vulnerable to cheaper/better technology that would undermine their rationale. One also wants the technology to be useful (i.e. has a business case at earlier, lower cost stages). For example, using VASIMR to more cheaply maintain the ISS orbit from decay due to drag, before building any fast Mars ship. Various beaming technologies – laser/microwave/PB might be useful in extending satellite lifetimes, or allowing maneuvering, or even perhaps providing high, but transient, power for some action, thus reducing the mass of onboard power supplies like solar cells. This might make a lot of sense for powering electric engines, hugely reducing propellant mass and the needed power supply. This allows scale up to provide power for larger facilities like space stations, again a possible business opportunity. This creates a sustainable model to allow more ambitious schemes. It also avoids capricious public funding that eventually sunk the manned space program. (It also ensures a more cost focussed program). If Glencore needed lunar resources for its mining business, there would be no issue about its funding and maintaining the necessary facilities and crew on the Moon, probably in concert with competitive suppliers.
One thing I always liked about Lubin’s roadmap was that his approach could be easily scaled and used for delivering payloads to a variety of destinations, not just 1 gm payloads to the nearest stars. If you can deliver smallish payloads to Mars in just a few days, rather than months, this can solve a variety of issues, allowing smaller expedition craft as they don’t have to bring everything along for every eventuality.
Miniaturization is going to be a key driver of what we can do, as this reduces costs. As we cannot make people smaller, it is one reason why I am convinced that robots are the key to opening up the solar system economy. They will be cheaper, and if sufficiently productive, far more profitable than humans.
I hate to be a downer on such an interesting concept, but I don’t see a mercury beamer being viable for Earth based launch. How much mercury does the system need and how much would be lost to the Earth’s atmosphere? Where would it end up and in what form? Add in realistic estimates for spills during handling and testing on the ground and I think environmentalists and lawyers would have a field day.
A space or lunar based system sounds like a much better idea.
Yes I would go ballistic myself!
I felt enthusiastic over the idea of being able to send a probe with 1 kg effective payload.
Even though it still would have to be a wonder of micro technology, to me it sound much more realistic.
Having it deployed i space would increase the cost a lot, even though this is only a preliminary study, with the enormous cost we should not split resources but go for the most effective alternative early on.
For me a space based system won’t be the answer. What orbit would it have? How far from Earth? How easy would it be to service and repair? How long would it last? The moon would be a permanent base. No orbital decay to worry about. I understand that we could use one of the Lagrange points but I think if we want a long term launch system it has to be on the moon. No atmosphere, no space clutter as around the Earth, and it can be paid for by an international consortium, as with the ISS (hopefully).
You make a very compelling argument Alex. I think for the inner System (essentially Mars and near Earth asteroids) we can hope for manned exploration as humans are still the most versatile, and capable method we have for moving, thinking and analyzing. But further out and especially for interstellar distances it surely must be carried out by robots and AI. I’m not convinced we’ll ever expend the resources needed to send out a generation ship or the like.
The challenges of generating and collimating a high amperage neutral beam sufficient to propel interstellar probes were well illustrated by Drs James Benford and Alan Mole.
Since I do not have advanced degrees nor relevant experience, I feel extreme confidence in the following proposal to address some of the challenge of neutral beam propulsion:)
The proposition is simple. Accelerate solid particles with suitable characteristics to the desired velocity needed to transfer a useful amount of momentum to the object of our affection (spacecraft bound for deep space in this case). The final velocity may be in the order of several hundred miles per second given the macro size of the proposed particles (ounces) so this concept may be limited to interplanetary travel. Of course, these particles/objects will not disperse from random transverse/thermal motion so collimination will be perfect. The key aspect here is that the momentum “flux” must be lessened as the object approaches the spacecraft. A small bursting charge or rapid controlled evaporation of volatiles in the object will produce a neutral cloud of particles (preferably entirely gaseous) of whatever diameter and length desired (hundreds of yards to several miles in diameter and ideally hundreds of miles long as may be required to efficiently interact with the sail). The particle would need some sort of mechanism to self-destruct on cue. Perhaps the particles can be smart enough to keep on the straight and narrow as they traverse interplanetary space.
As usually happens in well-researched fields, the foregoing has likely already been considered but still, it is entertaining to think about it and perhaps someone can add enough to it to make in interesting. A catchy name is needed so I propose the “shot gun drive”.
Ok, I concede on the lunar location for a laser or NPB device Alex. Your numbers are very convincing. Back to the drawing board for me :). However as you have pointed out there are significant hurdles to overcome for other locations. This won’t be solved easily but ultimately it will be an engineering problem, and those can usually be solved. I hope it goes well with these types of endeavours because they may be the only hope for human probes to reach nearby stars for a long time to come.
A Wild ‘Interstellar Probe’ Mission Idea Is Gaining Momentum
By Leonard David, Space.com’s Space Insider Columnist | January 9, 2019 at 06:54 am ET
https://www.space.com/42935-nasa-interstellar-probe-mission-idea.html
Can anybody post a link to the APL study referenced in the article?
Alex, I don’t find it online other than scattered references. Let me check with its author.
It has been pointed out on Facebook that this is the TAU interstellar probe mission from the 1980s revamped for the 21st Century.
https://en.wikipedia.org/wiki/TAU_(spacecraft)
“The 18 TW power needed would require 18 million such units.”
To me that says it all. That’s tantamount to saying no one will ever build this.
One way to geta near space environment without the need for a high throw cost to reach orbit is to float the beamer under a high altitude balloon. J P Aerospace’s idea of a high altitude (140,000 ft) floating platform might be a way to do this if scaled up to the needs of the beamer. This might also do away with the need for a laser to punch a hole in the atmosphere as the pressure at that altitude is around 1/1000th of sea level compared to around 50% on a Chilean high plateau. Or it might be held aloft by a high altitude dirigible, although at an altitude much lower than the edge of space platform.
What about the power supply?
Laser or microwave link from the ground, maybe.
The beam from air nased platform, that supposed to accelerate 1kg load up to speed 20000 km/s, approximately supposed to accelerate air based platform that has weight ~100000 kg up to speed ~200 m/s … (at least it will transfer to this platform supposed kinetic momentum, if we will take in account system efficiency real momentum will be higher, than this approximation)
Airbreathing jet to offset the forces maybe.
Or invent very quickly antigrvition engine :-)
Other words my numbers mean acceleration more than 11(m/c^2) i.e. ore than one g .
I.e. only energy losses will be twice more than for Earth based accelerator , here I do not take in account expence of this miracle airbrithing jet and it’s control loop.
I am sure that task to invent and build such massive high altitude air floating platform is many times more complicated task than neutral particle beam accelerator…
Air breathing jet engines have been around for a while, maybe even reaction engines design would do. I can’t see it weighing a huge amount, we get table top accelerators now days.
Ok, I will give alternative example 1000kg probe will get final velosity (after 18s) acceleration ~20km/s that if I remember numbers correctly faster that Voyagers and New Horizons have… If it is already here why it has not been used yet for Solar System exploration (question is ritoric) :-)
The article is interesting and it quotes Paul, but does it actually describe what type of propulsion system would be used for this precursor voyage out to about 1000 AU? I’m unclear about this. I like the idea in principle if it does indeed advance propulsion by a significant amount.
I know that solar sails with a close solar pass (‘sundiver’) missions have been considered, as have nuclear electric concepts. Let me check in with APL to see if I can get McNutt’s paper for us.
Here is McNutt’s NIAC proposal. Looks like a variety of propulsion concepts looked at – NTP, STP, and possibly a solar sail (see timeline).
https://www.scribd.com/document/161492114/McNutt-Ralph-Interstellar-Probe
You’re the numbers man Alex. What size balloon would be needed to lift a beamer of significant power output? It sounds like an interesting idea but is a mountain top more realistic as with advanced telescopes?
I think a balloon lift may only be feasible for a small test version.
Let’s start with the BEAR experiment. No mass is stated, but I found a reference that the launcher was an ARIES sounding rocket. Wikipedia gives its maximum payload as around 1500 kg. So that is the baseline.
A high altitude balloon calculator suggests that to lift this payload we need 1000 m^3 of helium (at 1 bar?) to reach 30km. So for 10 millibar at this al, I assume the He expands 100x. This would give an inflated balloon of radius 46m.
That is very large, and would only lift this 1.5 MT beamer to somewhere in the region of 30 km, less than that needed for the altitude we might want, yet at 1% of sea level air density and pressure.
My copy of “Floating to Orbit” (JP Aerospace) has their Dark Sky Station block 3 version with a lift volume of 2E9 cu. ft. Their DSS block 4 would carry 3x the load (6E9 cu ft?), and AFAICS, would be more than enough to run experiments on this size of beamer with a crew. Its intended altitude is 100,000 ft and air pressure is 1% of that at sea level.
[While I have never believed their idea of floating to orbit would work, my sense was that their high altitude floating research station has real merit. Much of the benefit of a space environment but without the 0 g, making the design of the living space much more conventional. The cost is much lower than for an orbiting station, and access is easier too – just take a balloon elevator. In an emergency, just enter a pressure vessel with a parachute. Currently, they launch small platforms under balloons for paid experiments and publicity.]
Testing a small beamer from high altitude would be much cheaper and one could test the whole system if a suitable craft could be launched into cis-lunar space as a CubeSat sized device that could deploy the loop and power it.
NASA’s high altitude balloon performance – altitude, lift mass.
https://www.nap.edu/read/12862/chapter/5#22
(see figure 3.1)
Atmospheric density, even at balloon altitudes, is still WAY too high to allow meaningful propagation of the beam.
Do you have some idea when atmospheric density is low enough to have insignificant effects? If 1% or even 0.1% is too high, this also suggests that any ground-based laser to punch a hole is going to have to be extremely effective. The laser is effectively creating a vacuum in a cylinder of about the same size as the NPB. I was of the impression that high power lasers ionize the air, rather than push it out of the way. I would have thought this must still leave a hot, thin plasma to keep the atmosphere at bay. Its density must be similar to that of the ionosphere where the BEAR experiment was done. Is that the case?
Thanks Alex. It does seem like a plausible concept for a test device.
Alex Tolley: Starshot estimates are that the laser beam would lose about 30% of its power in transiting through the atmosphere from a high-altitude low-humidity desert. No estimates have been made for a neutral particle beam preceded by a laser punching a hole for it. Without that laser the losses would be prohibitively high.
There is increasing interest in DOD in the neutral particle beam weapon approach. I don’t understand why the previous critiques of the method are not still relevant.
Calculations by Starshot about the possibility of a beam intercepting satellites show it to be a very low probability event. No doubt any satellite impacted by these intense beams would be destroyed. Nevertheless, one can simply fire when windows of opportunity occur.
I have not estimated the launch costs for putting a neutral particle beam system in space. Doubtless it would be prohibitive. That’s one reason why Starshot beams launch from the ground. For lower power pilot test purposes, use the same sort of strategy we’re following on Starshot: initial experiments would fire vertically to study stability of the sail on the beam. Once that is shown, one goes to horizontal high acceleration experiments in a long evacuated tunnel. Only later would experiments move to firing through the atmosphere at high-altitude.
Certainly the magsail itself can be tested separately from the neutral particle beam. Such independent development of the beam generation and the sailcraft is quite possible because there are many ways to produce a force on the magnetic field of the hoop. In fact, such experiments have been done over in the past decades.
Pointing accuracy is always a substantial requirement for interstellar missions. The state-of-the-art right now is micro-radian accuracy for tracking moving objects. Of course in astronomy, nanoradian accuracies are possible by staring at unmoving targets.
The idea of beaming from a high-altitude platform at ~20 miles it is attractive for getting above the atmosphere. Operating such a System carried by an enormous balloon and yet pointing the beam very accurately introduces new problems.
Eric S: Yes, the residual atmospheric density from laser hole punching must be very low for the neutral beam to propagate. Indeed, interaction with the atmosphere can cause the neutral atoms to be stripped of electrons. Stripping distance for GeV particles is quite long compared to the depth of the atmosphere.
The neutral beam has to be ionized in order to interact with the magnetic field of the hoop. No one has done the requisite calculations and simulations to decide how easy or how hard that would be.
Yes, the BEAM mission didn’t fully neutralize the ions, and produced both positive and negative ions as well. These charged particles rapidly repelled each other and got out of the beam. The idea of multiple bounces of the laser beam from the sail was first proposed by Geoff Landis, who is of the opinion that the effect can be used to multiply the acceleration by a factor of only a few. I’m considering using such an effect in the Starshot beam-riding and acceleration experiments.
Effects due to the Earth’s magnetic field will occur only for those particles which are charged.
Michael: Multiple reflections will give a factor of a few improvements; the requirement to have the reflectors carefully aligned is stringent, especially as the system will be vibration under high acceleration.
Gary Wilson: There are several thousand satellites around the earth, but the cross-section they represent is negligible. Putting the neutral beam system on the moon would be prohibitively expensive, as Alex Tolley has shown.
Ivan Vuletich: The amount of mercury mass involved is quite small actually. And mercury is widely available.
I believe the multi reflections is near 100 for an ideal system and the reflective tube does not have to be solid all the way along. Pointing and stability are par for the course.
As for a balloon an open vertical tube filled with hot hydrogen would work to lower the number of atoms in the way quite a bit, by about 10 to 20 times. With the Power been transmitted from the ground by microwave or laser.
Hot hydrogen as a lifting gas is a possible performance enhancer. The mass penalty to keep it hot might be an issue. Hydrogen is certainly easier to contain than helium. For a crew, the idea of “Hindenburg” might be a distraction… ;) Maybe best to keep this approach robotic.
For stability, you don’t want a vertical tube, but rather a horizontal one to avoid winds at different altitudes blowing in different directions, at least during ascent. At altitude, this arrangement may be OK. I would want some compromise to maintain stability, yet minimize the heating requirement. Perhaps ground microwave emitters to an absorber in the balloon’s lower surfaces?
The hot hydrogen only need be near 100 degrees, a microwave from the ground could do this. I still think the needle idea has some merit, each needle can be given a small variable charge, they can be made very dense and would easily punch through an atmosphere. Perhaps they could be filled with hydrogen which sublimes into space and interacts with the spacecraft.
https://www.advancedsciencenews.com/the-worlds-smallest-pipettes-capillary-action-in-carbon-nanotubes/
How does the Beam Generation Concept as described above relate to the much-talked -about ¨¨Wakefield Generator ´´ , which supposedly can be much more compact than traditional designs ? …
Fast beam of neutral atoms created using lasers and plasma.
Multi-step process removes electrons, accelerates ions, then neutralizes them.
Electrically charged particles are relatively easy to accelerate using electric and magnetic fields. Neutral particles cannot be steered in the same way, which is a bit disappointing, since they are useful experimentally due to their much greater ability to pierce target materials. A promising technique uses very short pulses of intense laser light to accelerate neutral particles, though up until now it has only achieved low energy transfer.
A new experiment has achieved neutral particle energies on the order of a billion times greater than prior efforts. R. Rajeev and colleagues managed this by accelerating particles while they were charged, and then transferring in electrons to neutralize the charge. This method has the advantage of being compact, and therefore useful for applications such as nanolithography; however, the authors argued their approach can be generalized for other purposes.
Laser acceleration works by bombarding atoms with light pulses to strip electrons off, creating a plasma—a neutral gas of ions and electrons. Since the electrons are a lot less massive than the ions, you can tune the laser pulses in a precise way that separates them. The electrons shoot off, leaving behind a gas of positively charged atoms moving in coherent waves.
As we all know from elementary school physics, like charges repel. So any positively charged particle added to the plasma will experience acceleration from the plasma waves. Laser plasma accelerators are more compact than many other accelerator designs, including those used in big experiments like the Large Hadron Collider (LHC), although they haven’t yet reached the same energies. Plasma acceleration (sans lasers) is also important in many astrophysical processes.
To adapt the method to neutral particles, the authors of the new study began with all the steps in the previous paragraph, using a plasma of argon atoms. However, the free electrons in the plasma were recombined with non-accelerated ions to create Rydberg atoms, in which electrons are only barely attached to the nucleus. Those loosely connected electrons were then transferred via collision to the rapidly moving ions from the accelerator, neutralizing them.
After applying powerful electric fields to separate out any residual ions, the researchers were left with a directed beam of highly energetic neutral atoms. By piggybacking on laser plasma acceleration, they achieved megaelectronvolt (MeV) energies, a billion times greater than previous efforts.
https://arstechnica.com/science/2013/01/acceleration-of-neutral-atoms-using-lasers-and-collisions/
This may be another problem: “Despite these difficulties, the idea of a neutral beam weapon was deemed potentially useful in at least one application – to destroy enemy satellites (as tested in the SDI BEAR project)”
Is Tesla’s particle beam weapon practical?
http://moreisdifferent.com/2015/01/13/is-teslas-particle-beam-weapon-practical/
We could use a torus balloon structure with a long vertical accelerator hanging in the middle. The torus shape will allow microwave energy to be transmitted from the ground efficiently to drive the machine as the structure would do well as a receiver. With the accelerator it could be a large vacuum tube with the accelerator parts in it. At the top we have a thin membrane heated to a very high temperature, this will allow the first impacts to easily go through. Once there is a small opening the stream of needles or particles the gas from outside will find it difficult to get into the vacuum tube. These needles offer an efficient way to be given a charge as they can be pre made and charged ready to go, the energy requirements to charge a needle with electrons is orders of magnitude lower that ionising.
If we use this type of system sensing a large amount of asteroids comes within reach.
https://arxiv.org/abs/1901.04422
Interstellar Probes: The Benefits to Astronomy & Astrophysics
Kelvin F Long
(Submitted on 11 Jan 2019)
Long range observations in the field of astronomy have opened up our understanding of the Solar System, the Galaxy and the wider Universe. In this paper we discuss the idea of direct in-situ reconnaissance of nearby stellar systems, using robotic probes.
In particular, we consider what additional knowledge can be learned that can only be obtained by such close encounters. This may include calibration of existing measurements, detailed observations of stellar winds, astrometry measurements of stellar parallax, refinement of our understanding of physics through the use of long baseline interferometers.
In addition, getting close to an exoplanet will enable detailed knowledge of planetary interiors, surface processes, geological evolution, atmospheric composition and climate, internal seismology, detailed surface morphology and even the speculative possibility of detecting the presence of microbial life, detailed palaeontology or even indigenous life-forms.
We argue that astronomical remote sensing should be pursued in parallel with in-situ reconnaissance missions by robotic probes, so that both can enhance the discoveries and performance of the other.
This work is in support of Project Starshot; an effort to send a Gram-scale probe towards another star at 0.2c within the next two decades, and return images and other data to the Earth.
Presented at the 47th IAA Symposium on Future Space Astronomy and Solar System Science Missions. Session on Space Agency Strategies and Plans.
Comments: 7 pages, 1 figure, 1 table, Presented at 47th IAA Symposium on Future Space Astronomy & Solar System Missions. Submitted to Acta Astronautica 19th December 2018
Subjects: Popular Physics (physics.pop-ph); Instrumentation and Methods for Astrophysics (astro-ph.IM)
Cite as: arXiv:1901.04422 [physics.pop-ph]
(or arXiv:1901.04422v1 [physics.pop-ph] for this version)
Submission history
From: Kelvin F Long [view email]
[v1] Fri, 11 Jan 2019 17:21:45 UTC (315 KB)
https://arxiv.org/ftp/arxiv/papers/1901/1901.04422.pdf
It would probably be better to just use a heavy particle bunch from the accelerator to punch a hole through the atmosphere than with a laser, it would be much more efficient to do so than with a laser.
It is always “good” idea to pollute our Earth athmosphere with heavy elements, Greenpeace (and me) will very “like” this consept…
Molybdenum or Platinum would do.