If Breakthrough Starshot is tackling the question of velocities at a substantial percentage of lightspeed, what do we do about the payload question? A chip-sized spacecraft is challenging in terms of instrumentation and communications, not to mention power. Enter Jeff Greason’s Q-Drive, with an entirely different take on high velocity missions within the Solar System and beyond it. Drawing its energies from the medium to deploy an inert propellant, the Q-Drive ups the payload enormously. But can it be engineered? Alex Tolley has been doing a deep dive on the concept and talking to Dr. Greason about the possibilities, out of which today’s essay has emerged. A Centauri Dreams regular, Alex has a history of innovative propulsion work, and with Brian McConnell is co-author of A Design for a Reusable Water-Based Spacecraft Known as the Spacecoach (Springer, 2016),
by Alex Tolley

Technical University of Munich for Project Icarus. Credit: Adrian Mann.
The interstellar probe coasted at 4% c after her fusion drive first stage was spent. It massed 50,000 kg, mostly propellant water ice stored as a conical shield ahead of the probe that did double duty as a particle shield. The probe extended a spine, several hundred kilometers in length behind the shield. Then the plasma magnet sails at each end started to cycle, using just the power from a small nuclear generator. The magsails captured and extracted power from the ISM streaming by. This powered the ionization and ejection of the propellant. Ejected at the streaming velocity of the ISM, the probe steadily increased in velocity, eventually reaching 20% c after exhausting 48,000 kg of propellant. The probe, targeted at Proxima Centauri, would reach its destination in less than 20 years. It wouldn’t be the first to reach that system, the Breakthrough microsails had done that decades earlier, but this probe was the first with the scientific payload to make a real survey of the system and collect data from its habitable world.
(sound of a needle skidding across a vinyl record). Wait, what? How can a ship accelerate to 20% c without expending massive amounts of power from an onboard power plant, or an intense external power beam from the solar system?
In a previous article, I explained the plasma magnet drive, a magsail technology that did not require a large physical sail structure, but rather a compact electromechanical engine whose magnetic sail size was dependent on the power and the surrounding medium’s plasma density.
Like other magsail and electric sail designs, the plasma magnet could only run before the solar wind, making only outward bound trips and a velocity limited by the wind speed. This inherently limited the missions that a magsail could perform compared to a photon sail. Where it excelled was the thrust was not dependent on the distance from the sun that severely limits solar sail thrust, and therefore this made the plasma magnet sail particularly suited to missions to the outer planets and beyond.
Jeff Greason has since considered how the plasma magnet could be decelerated to allow the spacecraft to orbit a target in the outer system. Following the classic formulations of Fritz Zwicky, Greason considered whether the spacecraft could use onboard mass but external energy to achieve this goal. This external energy was to be extracted from the external medium, not solar or beamed energy, allowing it to operate anywhere where there was a medium moving relative to the vehicle.
The approach to achieve this was to use the momentum and energy of a plasma stream flowing past the ship and using that energy to transfer momentum to an onboard propellant to drive the ship. That plasma stream would be the solar wind inside the solar system (or another star system), and an ionized interstellar medium once beyond the heliosphere.
Counterintuitively, such a propulsion system can work in principle. By ejecting the reaction mass, the ship’s kinetic energy energy is maintained by a smaller mass, and therefore increases its velocity. There is no change in the ship’s kinetic energy, just an adjustment of the ship’s mass and velocity to keep the energy constant.
Box 1 shows that net momentum (and force) can be attained when the energy of the drag medium and propellant thrust are equal. However this simple momentum exchange would not be feasible as a drive as the ejection mass would have to be greater than the intercepted medium resulting in very high mass ratios. In contrast, the Q-Drive, achieves a net thrust with a propellant mass flow far less than the medium passing by the craft, resulting in a low mass ratio yet high performance in terms of velocity increase.

Figure 1 shows the principle of the Q-Drive using a simple terrestrial vehicle analogy. Wind blowing through a turbine generates energy that is then used to eject onboard propellant. If the energy extracted from the wind is used to eject the propellant, in principle the onboard propellant mass flow can be lower than the mass of air passing through the turbine. The propellant’s exhaust velocity is matched to that of the wind, and under these conditions, the thrust can be greater than the drag, allowing the vehicle to move forward into the wind.
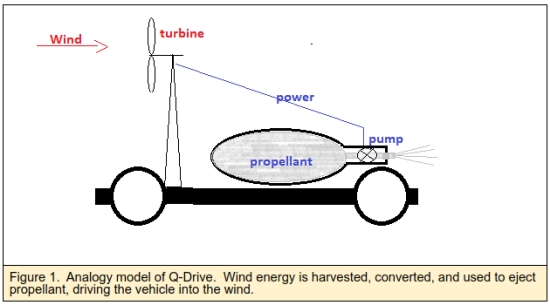
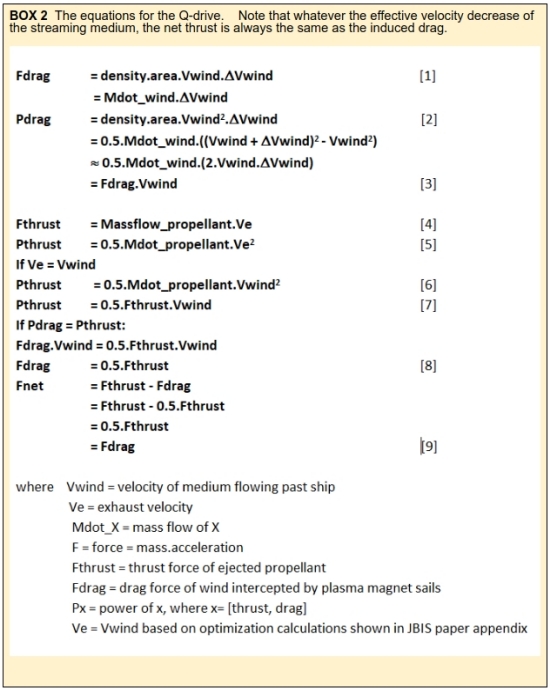
Box 2 below shows the basic equations for the Q-Drive.
Let me draw your attention to equations 1 & 2, the drag and thrust forces. The drag force is dependent on the velocity of the wind or the ship moving through the wind which affects the mass flow of the medium. However, it is the change in velocity of the medium as it passes through the energy harvesting mechanism rather than the wind velocity itself that completes this equation. Compare that to the thrust from the propellant where the mass flow is dependent on the square of the exhaust velocity. When the velocity of the ship and the exhaust are equal, the ratio of the mass flows is dependent on the ratio of the change in velocity (delta V) of the medium and the exhaust velocity. The lower the delta V of the medium as the energy is extracted from it, the lower the mass flow of the propellant. As long as the delta V of the medium is greater than zero, as the delta V approaches zero, the mass of the stream of medium is greater than the mass flow of the propellant. Conversely, as the delta V approaches the velocity of the medium, i.e. slowing it to a dead stop relative to the ship, the closer the medium and exhaust mass flows become.
Equations 3 and 7 are for the power delivered by the medium and the propellant thrust. As the power needed for generating the thrust cannot be higher than than delivered by the medium, at 100% conversion the power of each must be equal. As can be seen, the power generated by the energy harvesting is the drag force multiplied by the speed of the medium. However, the power to generate the thrust is ½ the force of the thrust multiplied by the exhaust velocity, which is the same as the velocity of the medium. Therefore the thrust is twice that of the drag force and therefore a net thrust equal to the drag force is achieved [equation 9]. [Because the sail area must be very large to capture the thin solar wind and the even more rarified ISM, the drag force on the ship itself can be discounted.]
Because the power delivered from the external medium increases as the ship increases in velocity, so does the delivered power, which in turn is used to increase the exhaust velocity to match. This is very different from our normal expectations of powering vehicles. Because of this, the Q-Drive can continue to accelerate a ship for as long as it can continue to exhaust propellant.
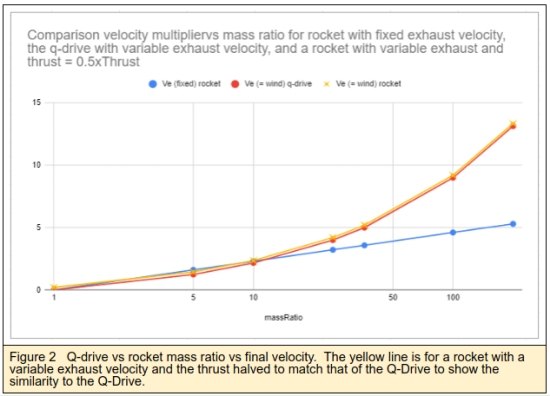
Figure 2 shows the final velocity versus the ship’s mass ratio performance of the Q-Drive compared to a rocket with a fixed exhaust velocity, and the rocket equation using a variable exhaust but with the thrust reduced by 50% to match the Q-drive net thrust equaling 50% of the propellant thrust. With a mass ratio below 10, a rocket with an exhaust equal to the absolute wind velocity would marginally outperform the Q-drive, although it would need its own power source to run, such as a solar array or nuclear reactor. Beyond that, the Q-drive rapidly outperforms the rocket. This is primarily because as the vehicle accelerates, the increased power harvested from the wind is used to commensurately increase the exhaust velocity. If a rocket could do this, for example like the VASIMR drive, the performance curve is the same. However, the Q-drive does not need a huge power supply to work, and therefore offers a potential for very high velocity without needing a matching power supply.
Equation A16 [1] and Box 3 equation 1 show that the Q-Drive has a velocity multiplier that is the square root of the mass ratio. This is highly favorable compared to the rocket equation. The equations 2 and 3 in Box 3 show that the required propellant and hence mass ratio is reduced the less the medium velocity is reduced to extract power. However, reducing the delta V of the medium also reduced the acceleration of the craft. This implies that the design of the ship will be dependent on mission requirements rather than some fixed optimization.

Box 4 provides some illustrative values for the size of the mag sails in the solar system for the Q-Drive and the expected performance for a 1 tonne craft. While the magnetic sail radii are large, they are achievable and allow for relatively high acceleration. As explained in [4], the plasma magnet sails increase in size as the medium density decreases, maintaining the forces on the sail. Once in interstellar space, the ISM is yet more rarefied and the sails have to commensurately expand.

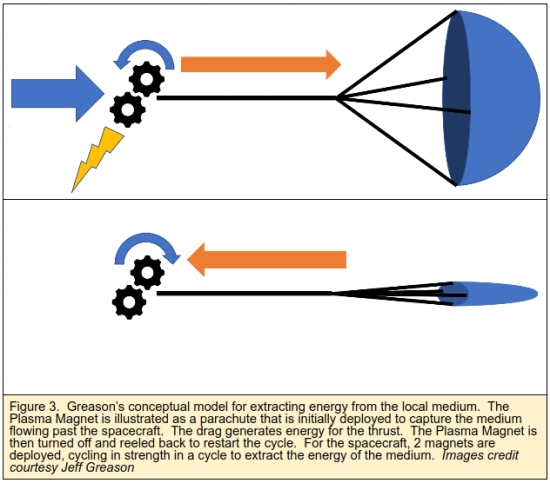
How might the plasma medium’s energy be harvested?
The wind turbine shown in figure 1 is replaced by an arrangement of the plasma magnet sails. To harvest the energy of the medium, it is useful to conceptualize the plasma magnet sail as a parachute that slows the wind to run a generator. At the end of this power stroke, the parachute is collapsed and rewound to the starting point to start the next power cycle. This is illustrated in figure 3. A ship would have 2 plasma magnet sails that cycle their magnetic fields at each end of a long spine that is aligned with the wind direction to mimic this mechanism. The harvested energy is then used to eject propellant so that the propellant exhaust velocity is optimally the same as the medium wind speed. By balancing the captured power with that needed to eject propellant, the ship needs no dedicated onboard power beyond that for maintenance of other systems, for example, powering the magnetic sails.
Within the solar system, the Q-Drive could therefore push a ship towards the sun into the solar wind, as well as away from the sun with the solar wind at its back. Ejecting propellant ahead of the ship on an outward bound journey would allow the ship to decelerate. Ejecting the propellant ahead of the ship as it faced the solar wind would allow the ship to fall towards the sun. In both cases, the maximum velocity is about the 400 km/s of the peak density velocity of the solar wind.
Can the drive achieve velocities greater than the solar wind?
With pure drag sails, whether photon or magnetic, the maximum velocity is the same as the medium pushing on the sail. For a magnetic sail, this is the bulk velocity of the solar wind, about 400 km/s at the sun’s equator, and 700 km/s at the sun’s poles.
Unlike drag sails, the Q-Drive can achieve velocities greater than the medium, e.g. the solar wind. As long as the wind is flowing into the bow of the ship, the ship can accelerate indefinitely until the propellant is exhausted. The limitation is that this can only happen while the ship is facing into the wind (or the wind vector has a forward facing component). In the solar system, this requires that there is sufficient distance to allow the ship to accelerate until its velocity is higher than the solar wind before it flies past the sun. Once past perihelion, the ship is now running into the solar wind from behind, and can therefore keep accelerating.
What performance might be achievable?
To indicate the possible performance of the Q-drive in the solar system, 2 missions are explored, both requiring powered flight into the solar wind.
Two Solar System Missions
1. Mercury Rendezvous

To reach Mercury quickly requires the probe to reduce its orbital speed around the sun to drop down to Mercury’s orbit and then reduce velocity further to allow orbital insertion. The Q-Drive ship points its bow towards the sun, and ejects propellant off-axis. This quickly pushed the probe into a fast trajectory towards the sun. Further propellant ejection is required to prevent the probe from a fast return trajectory and to remain in Mercury’s sun orbital path. From there a mix of propellant ejection and simple drag alone can be used to place the probe in orbit around Mercury. Flight time is of the order of 55 days. Figure 4 illustrates the maneuver.
2. Sundiver with Triton Flyby
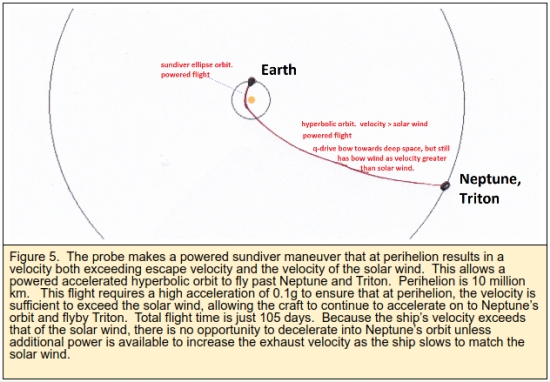
The recent Centauri Dreams post on a proposed flyby mission to Triton indicated a flight time of 12 years using gravity assists from Earth, Venus, and Jupiter.. The Q-Drive could reduce most of that flight time using a sundiver approach. Figure 5 shows the possible flight path. The Q-Drive powers towards the sun against the solar wind. It must have a high enough acceleration to ensure that at perihelion it is now traveling faster than the solar wind. This allows it to now continue on a hyperbolic trajectory continually accelerating until its propellant is exhausted.
This sundiver maneuver allows the Q-Drive craft to fly downwind faster than the wind.
For a ship outward bound beyond the heliosphere, the ISM medium is experienced as a wind coming from the bow, While extremely tenuous, there is enough medium to extract the energy for continued acceleration as long as the ship has ejectable mass.
Up to this point, I have been careful to state this works IN PRINCIPLE. In practice there are some very severe engineering challenges. The first is to be able to extract energy from the drag of the plasma winds with sufficient efficiency to generate the needed power for propellant ejection. The second is to be able to eject propellant with a velocity that matches the speed of the vehicle, IOW, the exhaust velocity must match the vehicle’s velocity, unlike the constant exhaust velocity of a rocket. If the engines to eject propellant can only eject mass at a constant velocity, the delta V of the drive would look more like a conventional rocket, with a natural logarithm function of the mass flow. The ship would still be able to extract energy from the medium, but the mass ratio would have to be very much higher. The chart in Figure 2 shows the difference between a fixed velocity exhaust and the Q-Drive with variable velocity.
The engineering issues to turn the Q-Drive into hardware are formidable. To extract the energy of the plasma medium whether solar wind or ISM, with high efficiency, is non-trivial. Greason’s idea is to have 2 plasma magnet drag sails at each end of the probe’s spine that cycle in power to extract the energy. The model is rather like a parachute that is open to create drag to push on the parachute to run a generator, then collapse the parachute to release the trapped medium and restart it at the bow (see figure 3). Whether this is sufficient to create the needed energy extraction efficiency will need to be worked out. If the efficiencies are like those of a vertical axis wind turbine that works like drag engines, the efficiencies will be far too low. The efficiency would need to be higher than that of horizontal axis wind turbines to reduce the mass penalties for the propellant. It can be readily seen that if the efficiencies combine to be lower than 50%, then the Q-Drive effectively drops back into the regime illustrated in Box 1, that is that the mass of propellant must become larger than the medium and ejected more slowly. This hugely raises the mass ratio of the craft and in turn reduces its performance.
The second issue is how to eject the propellant to match the velocity of the medium streaming over the probe. Current electric engines have exhaust velocities in the 10s of km/s. Theoretical electric engines might manage the solar wind velocity. Efficiencies of ion drives are in the 50% range at present. To reach a fraction of light speed for the interstellar mission is orders of difficulty harder. Greason suggests something like a magnetic field particle accelerator that operates the length of the ship’s spine. Existing particle accelerators have low efficiencies, so this may present another very significant engineering challenge. If the exhaust velocity cannot be matched to the speed of the ship through the medium, the performance looks much more like a rocket, with velocity increases that depend on the natural logarithm of the mass ratio, rather than the square root. For the interstellar mission, increasing the velocity from 4% to 20% light speed would require a mass ratio of not just 25, but rather closer to 150.
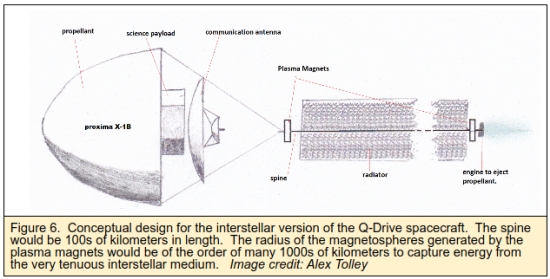
Figure 6 shows my attempt to illustrate a conceptual Q-Drive powered spacecraft for interstellar flight. The propellant is at the front to act as a particle shield in the ISM. There is a science platform and communication module behind this propellant shield. Behind stretches a many kilometers long spine that has a plasma magnet at either end to harvest the energy in the ISM and to accelerate the propellant. Waste heat is handled by the radiator along this spine.
In summary, the Q-Drive offers an interesting path to high velocity missions both intra-system and interstellar, with much larger payloads than the Breakthrough Starshot missions, but with anticipated engineering challenges comparable with other exotic drives such as antimatter engines. The elegance of the Q-Drive is the capability of drawing the propulsion energy from the medium, so that the propellant can be common inert material such as water or hydrogen.
The conversion of the medium’s momentum to net thrust is more efficient than a rocket with constant exhaust velocity using onboard power allowing far higher velocities with equivalent mass ratios. The two example missions show the substantial improvements in mission time for both and inner system rendezvous and an outer system flyby. The Q-Drive also offers the intriguing possibility of interstellar missions with reasonable scientific and communication payloads that are not heroic feats of miniaturization.
References
1. Greason J. “A Reaction Drive Powered by External Dynamic Pressure” (2019) JBIS v72 pp146-152.
2. Greason J. ibid. equation A4 p151.
3. Greason J. “A Reaction Drive Powered by External Dynamic Pressure” (2019) TVIW video https://youtu.be/86z42y7DEAk
4. Tolley A. “The Plasma Magnet Drive: A Simple, Cheap Drive for the Solar System and Beyond” (2017) https://www.centauri-dreams.org/2017/12/29/the-plasma-magnet-drive-a-simple-cheap-drive-for-the-solar-system-and-beyond/
5. Zwicky F. The Fundamentals of Power (1946). Manuscript for the International Congress of Applied Mechanics in Paris, September 22-29, 1946.



Q-Drive : I don’t understand how it works …
Then I failed *sigh*. If it is any compensation, Greason says that it may take a few attempts to understand it. Initially, I was very skeptical and it took time, carefully working through the equations, clarifications, and modeling with code for me to accept that it would work in principle. The hardest part for me was the acceptance of the drag equation.
I got lost at the very beginning. What does m_dot stand for?
mass flow, or mass/time.
The purpose here is to convert momentum to force (thrust/drag) and energy to power.
Aah, OK, so the _dot is a derivative. I suggest that for the next article you use a proper math typesetting software, like LaTeX or lout.
I will consider that. Probably the simpler solution is just to define any terms first. I used the dot notation to avoid the dX/dt form that is clumsy and difficult to format easily.
This is a bit late, but perhaps Paul would be interested in enabling MathJax (mathjax.org) on the site? Then typesetting equations using relatively simple languages like TeX or ASCIIMath and browser-side resources should be achievable.
A good idea, I think, and thanks for this. I’ve played around with various equation editors but haven’t really had the time to explore them. Will keep this in mind.
So in reviewing the comments I came to the conclusion they what this method amounts to is sucking the interstellar medium of its energy and dumping it into propellent; is that the essence of this whole thing?
“Technical University of Munich for Project Icarus. Credit: Artist unknown.”
I think it’s made by Adrian Mann.
https://www.spaceanswers.com/futuretech/solar-probe-plus-nasas-sun-skimming-spacecraft/
Sorry, wrong link: https://www.spaceanswers.com/futuretech/ghost-ship-to-alpha-centauri1/
Yes, it looks like you have found the correct image and credit.
Paul, can you modify the credit for the header image to Adrian Mann?
Done.
Thanks for the suggestion, but I cannot confirm the artist.
How does this compare in performance to Zubrin-Brisbin’s dipole drive?
Both drives are so speculative that relative performance measures are of little value. However, I would say that the plasma magnet as a drag device gas such a low mass compared to other devices that need physical meshes to interact with the medium, that all things being equal, the Q-Drive theoretically could have a higher upper bound to performance. But as I say, this is purely speculative as there is no empirical proof of either drive performance, either of which could be that they “don’t work in practice”.
I see some problems here. In the first design, the analogy of the Q drive, the turbine looks like a wind power propeller used in our thick Earth’s atmosphere with a surface pressure average of 1000 millibars. The rarefied solar wind could not turn such a turbine so I don’t see how that would work.
With the conceptual version of the interstellar Q drive has a problem. The propellant tank is too far away from the electromagnet. How can the propellant move to the electromagnet to be accelerated without some of it being lost to the ISM. Consequently I can’t see how this design would work efficiently enough to have any acceleration. This design might need some changes before it could actually work. If we look at VASIMR, it’s propellant is heated and injected directly into the the magnetic field without any escaping into the ISM before it is accelerated.
The toy model is simply to explain the overall concept as an analogy. It is like the wind turbine boats that can sail upwind. The suggested drive uses the Plasma Magnet technology to extract power from the medium as it streams past and to use that power to eject propellant. The math then clothes the physics.
There are 2 Plasma Magnets, one at each end of the ship’s spine. They modulate their respective magnetospheres to create a moving magnetic field. This acts as a wind turbine. The magnetic fields also accelerate the propellant down the spine.
I would argue that the detail of where the propellant tank is located is very minor compared to the challenges of making this drive work. It is the concept that is intriguing as it allows for a craft to accelerate without requiring onboard power, a problem for electric engines like VASIMR and even the possible increases in the thrust of next-generation ion drives.
The analogy is enough to see why this simply will not work.
I did reach fig 1, and then gave up reading.
Just imagine anyone would build a wind turbine on their electric car and stating it will recharge the batteries as you drive.
Then the fact to reach 20C for practically nothing.
Interstellar flight is possible, but it will not be with a TANSTAAFL drive. (There ain’t no such thing as a free lunch.)
Your analogy isn’t the same, although I understand it. You do need to understand why the drag and thrust forces are different, even though the kinetic energy and power must be the same. It took me some time to see why this was possible before I was able to accept it.
But even if you remain skeptical, my example in BOX 1 should be enough to show that a very inefficient way to use propellant will work to drive a craft into the “wind” and accelerate, invalidating the appropriateness of your analogy (which I agree with). The Q-Drive is just a much more effective way to create the imbalance of forces with relatively efficient use of propellant, certainly more efficient than a fixed exhaust velocity rocket that I show in figure 2.
Could a variant of the Dyson-Harrop power satellite be used for the energy capture section of the drive ?
https://www.lpi.usra.edu/meetings/abscicon2010/pdf/5469.pdf
http://articles.adsabs.harvard.edu//full/2010IJAsB…9…89H/0000089.000.html
I am not familiar with this. However, I see no viable means to increase the power as the ship increases velocity, nor a means to beam power to it easily while traveling in interstellar space. A key point of teh drive is that it obviates the need for a special, high power source of energy to run the drive.
1. The task to collect energy from ISM is exactly same task as “creating technology for controlled thermonuclear fusion”. Not more and not less…
2. A parachute “propulsion” example – also to speculative, it seams that you need to spend much more energy to catch ISM plasma, than you can collect from ISM, so we can suppose that ISM here unneeded detail…
See above notes related to controlled thermonuclear fusion.
We do know that the external medium does cause a drag force. Both the Earth’s magnetosphere is deformed by the solar wind, and the sun’s heliosphere is deformed by the flow of the ISM (although its shape is unknown, and see A New Shape for the Heliosphere. The power for the plasma magnet is quite low (in principle) as it utilizes the ion medium to extend its own magnetosphere. The real issue is how efficiently power can be extracted from the ISM as it streams past the ship. If the efficiency is insufficient, it will have a similar problem as the Bussard ramscoop ship. That design proved to experience higher drag forces than thrust. In the case of the Q-Drive, the medium-to-propellant ratio would fall to levels that would result in impractical large mass ratios, just like a rocket.
Yes, I was reminded of the Bussard ramscoop when I read this. Buts this is new and the effort that has gone into imagining and developing it is to be applauded. My understanding of the driving ethos of ‘Centauri Dreams’ and Tau Zero is that they were conceived as a forum to imagine and discuss ways of traveling to the stars ( or somewhere in between atleast ) . Ideally within the timeframe of a human life span.
As Alex points out the ongoing problem with all current and “near future” drive concepts continues to be the mass vs velocity conundrum, More velocity requires more fuel/propellant/reaction mass = more mass which requires more fuel/propellant/reaction mass and so on and so on. Even for more exotic concepts such as nuclear fusion and antimatter.
Warp drives and wormholes require unobtainium , phlogiston and pulp fiction to work and can be ( regretfully ) discounted. So the fact remains that in order to break the cycle above and create a genuine “real time” interstellar craft ( as opposed to an Ark/generation ship), the environment in between the stars will have to be exploited in some way or other. You don’t get “owt for nowt” as they say in Yorkshire ( “ought for nought” elewhere in the English speaking world !) . Maybe so, but there’s nothing to stop you getting ” owt from not quite nowt” . Assuming there is enough “no quite nowt”. Be it the interstellar medium, solar wind or some other more nebulous premise such as quantum vacuum energy. So I applaud all novel propulsion systems. Most if not ( quite ? ) all of which will be debunked. But the history of science and technological development is based on 99% failure.
Because if we don’t try, we don’t get and one day , just one day, one of these ideas might actually be shown to work. No warp factor 9.5 to the Typhon Sector admittedly, but anything around 0.2c or so would do very nicely thanks very much.
So well done Dr Greason et al and keep going.
Either you have not explained how you are extracting energy from the ISM, and chosen terrible analogies, or this does not work.
As you say, the force of thrust equals the force of drag. F=ma, but your F = 0. No net force, no acceleration.
You ask, where does the kinetic energy go? The answer is that you’re “grabbing” the ISM and pulling it along with you. Equal and opposite reactions. As much energy as you lose from the drag force, the ISM gains.
I don’t believe it matters how good your conversion efficiencies are, the Q-Drive goes nowhere.
The toy model is understandable, I thrust as we understand how wind turbines work.
The parachute analogy is more like an anemometer, or a vertical axis wind turbine.
No. The energy, and hence power, or the medium cannot be smaller than the energy/power of the propulsion. However, the forces are different and in the formulation used, the thrust force is 2x teh drag force. Therefore the net thrust force = drag force and the drive will accelerate the craft into the medium.
No. When teh wind velocity has a small decrease, the energy and momentum are barely changed. IOW, there is little drag force. The thrust is due to ejecting mass which effectively concentrates the momentum into the remaining ship’s mass. Greason needs the energy to be gained from teh ISM to be like a horizontal axis wind turbine where the power due to lift forces is far higher than teh drag forces from any reduced wind speed behind teh turbine. Whether the model to extract energy achieves this is another issue, but Greason is sure that there are a number of ways to develop the equivalent of high lift-to-drag ratio devices to harvest the energy of the medium.
Yes, it was also my automatic reaction to this, that it simply will not work.
I am in isolation so if anyone will post the actual math behind this here I got time to go trough and will post my analysis of their study.
The best place to start is Greason’s JBIS paper in the references. All the calculations are in that paper, especially in the appendix.
One would need a large amount of the interstellar gas to make an efficient fusion reaction like the Bussard ramjet, the spacecraft would need to be bigger in the front to scoop up the rarefied gas. Also I don’t see much thrust pressure with this design. How would it leave orbit and Earth’s gravity well which is why I said I think the design needs some refinement. How does the electromagnet in the back efficiently get the gas from the ISM when the propellant tank in the front deflect the interstellar gas and the back collisions of gas would have to be perpendicular and also grazing angle to the direction of the spacecrafts flight?
Low thrust ion drives and solar sails can leave orbit by a slow spiral that extends teh orbit and vehicle speed. Using bold values, my 2 examples show that a Q-drive vehicle might achieve 1/100th and 1/10th of a g depending on mass ratio.
Bear in mind that in the solar system, the craft needn’t travel into the solar wind for all maneuvers, but rather perpendicular in some cases, limiting the drag forces in the forward direction. I tried to show that in the image depicting the Mercury rendezvous flight.
The idea initially seems plausible in that (in the frame of reference of the medium) the kinetic energy and momentum is being “concentrated” into the non-propellant part of the probe. This seems like the time inverse of a collision between a small probe and a large mass of propellant that links them together – which needs to be an inelastic collision to satisfy both conservation laws, which is worrisome. However, the inelastic collision doesn’t take into account the presence of the medium as a third player.
The math above is a little hard to follow, so to take a stab at it from scratch (no warranties express or implied): if we work the above example and use a non-relativistic approximation (or use rapidity instead of velocity) then the kinetic energy relative to the given rest frame goes from .04*.04*50000 = 80 c*kg^2 to .2*.2*2000 = 80 … but momentum drops from .04*50000 = 2000 c*kg to .2*2000 = 400. If the remaining momentum is going into the medium, it isn’t in the kinetic energy budget. I suppose the particles of the medium could be moving in the opposite direction to the probe in the given frame of reference at a velocity = -x and are changed to be moving the other (same) way (velocity = x). That would keep their KE constant in our frame while absorbing momentum, but it requires 1600*(c/2x) kg of medium to be modified this way. Do I have that right?
Mr. Serfas, I believe you’ve got it.
In essence, it’s a progressive series of inelastic collisions between little packets of reaction mass and the surrounding medium, with the “excess energy” shed in the inelastic collision going back in to the ship. So the kinetic energy (or as much of it as you can manage, at any rate) stays in the ship, and the excess momentum of the shed reaction mass is carried away by the wind.
Not every year it happens, to see an interstellar drive concept which is entirely new (for me) AND might work. Very impressive!
The energy conversion system must be as direct as possible, to achieve the needed efficiencies. But it seems to me, while Q-drive requires a lot of innovative thinking, the high efficiency is possible in principle.
…I imagine the central shaft filled with plasma from propellant, and some sort of travelling waves induced in it by magsail-like device, which couples it to wind, or something like this…
OTOH, the designs and limitations may have much in common with the Bussard ramjet. If it is shown that the nature of medium implies some sort of inevitable high losses, it would apply to Q-drive as well.
In addition, the 0.2c speeds are comparable to the limit of “conventional” direct exhaust thermonuclear rocket with high mass ratio. Even if someone designs a feasible wind-propellant energy conversion system, Q drive might not win without having some additional advantages.
The sheer universality of the principle is beautiful. If someone demonstrates it even running on tracks or flying in the atmosphere, it will be impressive on it’s own, which will fuel the researches and thinking.
Where the Q-Drive excels in principle is the vastly lower mass ratio needed to achieve a specified terminal velocity as shown in figure 2. This is because the exhaust velocity increases with teh ship’s velocity, rather than remaining fixed in the rocket equation. The propellant can also be inert, although in practice it would need to be easily accelerated electrically or magnetically. Even fusion drives for interstellar flight have huge fuel/propellant tanks. See the BIS Daedalus for example or David Hardy’s paintings of Enzmann starships. Enzmann starship>
Greason has suggested it might be used for high Mach number atmospheric flight. Creating a working version of the toy model might be a nice project while we have spare time self-isolating at home. ;-)
I was thinking of traveling wave tubes myself; Depending on phase velocity, they can function to either extract power at the cost of drag, or consume power while accelerating particles.
The catch is that they only interact with charged particles; We’re fortunate that we’re currently moving through an ionized bubble in the medium, most of it is neutral.
The problem with ion power or electric engines is that although they have a high specific impulse, the thrust is low so there is no way for a electric engine to leave Earth’s gravity well or Earth orbit without the help of a high thrust engine to help it like a conventional liquid or solid fuel rocket. VASIMR can do that because it has a low specific impulse and high thrust, so it can leave Earth orbit. It also can have a high specific impulse, high exhaust velocity.
A low thrust also has a slow acceleration. VASIMR heats it’s fuel or gas up to one million degrees centigrade and more particles are being accelerated and shot through the electromagnetic field at one time as a result so it has the greater thrust.
One might have a long wait for an electric engine to get to 20 percent C if it is even possible for that type of design to do that. It works on Star Trek. The Q drive is nothing new, but a glorified, giant ion drive or electric engine. Adding solar wind wont change it’s velocity, or thrust unless you add a giant solar sail due to the solar wind being rarefied gas.
1. I’m worried about how any interstellar craft handles interstellar debris larger than a pebble.
2. More fancifully…I don’t claim to understand it all, but it would be exciting to see how the craft navigates the outer reaches of red giants like Betelgeuse. (I know, that won’t be for a few thousand years yet, but still…)
Interstellar craft generally handle interstellar debris larger than a pebble by just not having really bad luck. The density of the interstellar medium is extremely low, and subject to a power law on particle mass. The odds of hitting something as massive as a pebble are extremely low, unless you were to do something like fly through a planetary nebula.
You really have to just be prepared for a continual influx of atoms and molecules, and occasional dust grains, and hope to survive hitting something as big as a grain of sand. And treat collisions with pebbles as an unavoidable but extremely unlikely bad roll of the dice.
Isn’t there the problem that the interstellar medium (ISM) might not be dense enough to make this idea work? And what if ISM density is uneven throughout the galaxy and the Q ship sails through a low density region? To use a sailing analogy, it seems to me that a Q Drive ship could end up “becalmed” in space. Of course it wouldn’t stop moving due to inertia, but it would still have a big problem. So what do the proponent of Q Drive have to say about this?
In theory, the size of the magnetic sail increases as the ion density declines (as long as there are ions). This makes teh plasma magnet sail attractive compared to physical electric or magnetic sails. However, this has not been tested beyond small scale (really small!) laboratory experiments that assume scaling applies.
As you point out, there is no equivalent of being becalmed, as there is no drag if the medium is absent. All that happens is that the thrust and propellant use drop to zero and the craft maintains its velocity.
This is one reason why it is important to run tests of the plasma magnet outside teh Earth’s magnetosphere to determine its performance and constraints. The cost of a plasma magnet is very low and a small version could be placed in a CubeSat. Unlike most CubeSat missions, the plasma magnet does need to be placed in an orbit beyond the Earth’s magnetic field to run the tests. This will be costly unless there is a free piggyback ride available in such an orbit. If the plasma magnet does not work, then the Q-Drive will need another way to extract power from the kinetic energy of a thin medium that is both efficient and low mass.
Ironically, in science news lately is mention of plasmoids in space, generated as pieces of planetary magnetospheres are shed under the drag of the solar wind.
You’d expect this to happen to plasma magnets, too. I suspect that, in practice, these blown magnetic bubbles will just get blown away from the magnet generating them, long before they grow large enough to provide the performance we hope for.
Either physical tests or high resolution simulations are needed here.
wind powered terrestrial vehicle going upwind
So it’s possible that it would work. It would seem that it has too many, too frequently moving parts. A bit Rube Goldberg-ish to me, since I do not understand stuff from Shinola in this matter.
The vehicle you link to is critically dependent on having the ground to work against. Just like a sailboat tacking into the wind needs the water to work against.
That’s what bothers me about this proposal: There’s only the ship and the interstellar medium, no “ground”. I’ve run the numbers and it does seem to work, but I can’t shake the feeling that’s because of some subtlety that’s being overlooked.
So I’ve requested the paper to have a closer look at it.
In any case, reaching 50% end to end efficiency would be very challenging indeed, even if the physics work out.
The story of “downwind faster than the wind” is fascinating. Videos showing the turbine at the transition point as the vehicle velocity goes through the wind speed is fascinating. While the upwind experiment is interesting, it is not as dramatic as downwind. Well worth following the story, watching the toy demos (on a walking machine and a fan) and then building the Blackbird.
I think it would be a fun project to build a toy vehicle as shown in figure 1 as this is different from the sailboat designs that use a wind turbine to power a propeller.
Whether this can be achieved in space with charged particles like the solar wind is still to be determined. While the Plasma Magnet would be the most efficient in terms of thrust to mass ratio, it would be interesting if other magsail or electric sail technologies would work too using this approach. It is dependent on the power to drag ratio of the power extraction mechanism and the efficiency of the energy conversion to thrust.
Perhaps I am drawing conclusions to quickly and/or lazy and may have been too slow to comment but a few points to ponder:
– put the Q-boat and the ISM in a huge black box
– the net momentum of all masses in the black box must be conserved
– the momentum hence velocity of the ISM passing through the box must be reduced to extract energy for the Q-boat
– the Q-boat and its ejected propellant must add momentum to equal the reduction of the momentum in the ISM to conserve momentum
– kinetic energy is a function of ?V^2
– the kinetic energy change in the ISM must be smaller than the kinetic energy gain of the Q-boat
– the law of conservation of energy is violated.
There are a few gaps in the above analysis but the point is that the Q-boat seems to violate the law of conservation of energy. Put another way, lets have a Q-boat shooting off to Triton arriving at a high velocity. Its kinetic energy is captured by some means. Then the Q-boat is shot back at its origin and again gains velocity with the corresponding kinetic energy captured again. The Q-boat is shot back and forth, retracing its path each time, and gains energy each time – perpetual motion.
–
This is a pretty neat idea, although I will have to reread this a couple times to make sure I buy this isn’t breaking thermodynamics or momentum conservation in some way.
I mainly wanted to point out that particle accelerators are actually extremely efficient. Old copper accelerators can operate in the +40% efficiency regime and superconducting machines can push far higher (approaching 90% in some cases). The bigger problem is probably just in actual mass through-put. Accelerators do not eat mass at a high rate and increase that feed rate to something rocket like will be hard.
“The second issue is how to eject the propellant to match the velocity of the medium streaming over the probe. ”
This is the focal issue if the proposal works. Efficient particle accelerator might be the only logical option. Even a fission fragment rocket expels ‘propellant’ at 5%C tops.
Even if everything else works in the proposal, without this being solved it might end up the way of bussard ramjet. Working in principle only.
However otherwise it might definitely be a near term reasonably high TRL solution to a outer solar system and early heavy interstellar probes.
For anyone confused about the concept; highly suggested to watch the TVIW presentation on the concept.
3. Greason J. “A Reaction Drive Powered by External Dynamic Pressure” (2019) TVIW video https://youtu.be/86z42y7DEAk