I see that Erik Lentz (Göttingen University) has just begun a personal blog, something that may begin to attract attention given that Dr. Lentz has offered up a new paper on faster than light travel. At the moment, the blog is bare-bones, listing only the paper itself (citation below) and an upcoming online talk that may be of interest. Here’s what the Lentz blog has on this:

Upcoming online talk to be given on 18 March 2021 at 3pm Eastern Standard Time for the Science Speaker Series at the Jim and Linda Lee Planetarium: https://youtu.be/6O8ji46VBK0

I checked the URL and found the page with a countdown timer, so I assume the event is publicly accessible. I would imagine it will draw a number of curious scientists and lay-people.

On the subject of faster than light travel, much of the work in the journals has evolved from Miguel Alcubierre’s now well known paper “The Warp Drive: Hyper-fast travel within general relativity,” which presented the idea of a ‘bubble’ of spacetime within which a volume of flat space could exist. In other words, it might be possible to enclose a spacecraft within such a bubble. While there is a physical restriction on objects within spacetime moving faster than the speed of light, spacetime itself is theoretically capable of expansion without limit — this is essentially the notion of ‘inflation’ that drives most current thinking about the earliest moments of the universe.

Alcubierre’s paper ran in May, 1994 in the prestigious journal Classical and Quantum Gravity, a venue whose demanding standards of peer review and acceptance give it high credibility. In other words, papers in this journal rightfully attract attention because of the demanding requirements of publication. I had more or less overlooked the new paper by Dr. Lentz until I realized that it was published here, after which I began to take notice.

This does not mean, of course, that either the Alcubierre ‘warp drive’ concept or the much different ideas of Erik Lentz can ever be engineered, but it does offer a great deal of interest from the standpoint of the mathematics of warped spacetime. After the Alcubierre paper, much of the ongoing work has been involved in exploring how negative energy operates, for ‘negative energy density’ is exotic and vast amounts would be required to form the needed ‘bubble’ of spacetime. The Lentz paper does away with negative energy. I’m hearing it described as an idea more in conformance with conventional physics, though that may also need clarification.

The essential notion put forward by Dr. Lentz is that there are configurations of spacetime curvature that can be explored as ‘solitons,’ which are a solution he deems physically viable, and thus not dependent on negative energy at all. Here we’re already in deep water. A soliton, as I have been learning, is a wave that can retain its shape and move at constant velocity. That such curiosities are within the realm of physical possibility is made clear by the origin of the study of solitons. They actually go back to an observation by British engineer John S. Russell in 1834. In a famous and oft-quoted passage delivered ten years later to the British Association for the Advancement of Science, Russell had this to say about what he called a ‘wave of translation’:

I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped – not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then suddenly leaving it behind, rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon which I have called the Wave of Translation.

Thus was born the study of solitons, which now extends into nuclear physics, optics and other fields, now including exotic propulsion. Notice that what Russell describes is a wave that is stable and can travel. His use of the word ‘translation’ means that this is not a wave made up of the same water that travels the length of the channel he was observing, but rather a wave that moves through the medium. Water is moving but being displaced in the process. We can think of the wave of translation — or at least I’ve seen it referred to this way — as a ‘wave packet’ that can maintain its shape, as it did in Scotland’s Union Canal for Russell.

I turned to Hilborn and Cross’ Chaos and Nonlinear Dynamics (Oxford University Press, 2000) to see solitons described as ‘nonlinear wave phenomena.’ Thus:

A soliton is a spatially localized wave disturbance that can propagate over long distances without changing itsshape. In brief, many nonlinear spatial modes become synchronized to produce a stable localized disturbance.

Solitons turn out to be remarkably stable. A great deal of mathematics has gone on since as solition concepts evolved, all much beyond my pay grade. I looked again at Dr. Lentz’ website to get a notion of what he was proposing in his own words, because I find it hard to make the considerable jump from the early observations of Russell to today’s understanding of solitons. Here’s Lentz with a vest-pocket description of faster than light travel that does not violate Einsteinian relativity:

Hyper-fast (as in faster than light) solitons within modern theories of gravity have been a topic of energetic speculation for the past three decades. One of the most prominent critiques of compact mechanisms of superluminal motion within general relativity is that the geometry must largely be sourced from a form of negative energy density, though there are no such known macroscopic sources in particle physics. I was recently able [to] disprove this position by constructing a new class of hyper-fast soliton solutions within general relativity that are sourced purely from positive energy densities, thus removing the need for exotic negative-energy-density sources. This is made possible through considering hyperbolic relations between components of the space-time metric’s shift vector. Further, these solutions are sourceable by a classical electronic plasma, placing superluminal phenomena into the purview of known physics. This is a very exciting breakthrough that I hope to have more [to] report on soon.

I take this to mean that there are mathematical solutions for spacetime curvature that use solitons as the mode of organization. Alcubierre’s ‘warp bubble’ becomes, in soliton mode, a wave that maintains its shape and moves at constant velocity. The key here, Lentz believes, is that this is a way of altering spacetime geometry without the use of exotic negative energy. Moreover, Lentz’ equations evidently show that tidal forces within the bubble can be minimized. The passage of time inside the soliton can be adjusted to match the time outside the bubble.

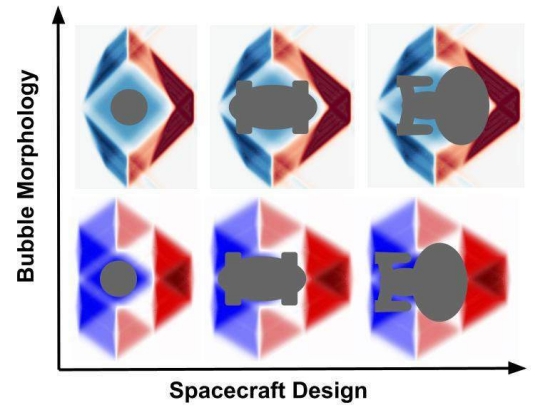
Image: Artistic impression of different spacecraft designs considering theoretical shapes of different kinds of “warp bubbles.” Credit: E Lentz.

We would still need enormous amounts of energy, but we are dealing with the kind of energy we understand rather than the far more amorphous ‘negative energy.’ Here’s Lentz again:

“The energy required for this drive travelling at light speed encompassing a spacecraft of 100 meters in radius is on the order of hundreds of times of the mass of the planet Jupiter. The energy savings would need to be drastic, of approximately 30 orders of magnitude to be in range of modern nuclear fission reactors… Fortunately, several energy-saving mechanisms have been proposed in earlier research that can potentially lower the energy required by nearly 60 orders of magnitude.”

Such energy savings methods would be prodigious indeed and it is to these that Dr. Lentz apparently turns next. The paper is Lentz, “Breaking the Warp Barrier: Hyper-Fast Solitons in Einstein-Maxwell-Plasma Theory,” Classical and Quantum Gravity Vol. 38, No. 7 (March, 2021). Abstract. We are in very deep mathematical waters here, so all I want to do is point to the paper and urge those interested to take in Dr. Lentz’ talk on the 18th.