It’s a measure of how common exoplanet detection has become that I can’t even remember the identity of the object I’m about to describe. Back in the early days (which means not long after the first main sequence detection, the planet at 51 Pegasi), I was at a small dinner gathering talking informally about how you find these objects. A gas giant was in the news, another new world, or was it really a brown dwarf? And just what was a brown dwarf in the first place? Back then, with just a handful of known exoplanets, introducing the idea of a brown dwarf raised a lot of questions.
Now, of course, we have planets in the thousands and are just opening up the discovery space. Brown dwarfs are plentiful, with some estimates at one brown dwarf for every six main sequence stars. A 2017 analysis of a cluster called RCW 38 by Koraljka Muzic and team concluded that the galaxy contains between 25 and 100 billion brown dwarfs. So we have plenty to work with as we home in on the still controversial borderline between planet and brown dwarf, as well as between brown dwarf and star.
We know that brown dwarfs are not massive enough to support hydrogen fusion but do fuse small amounts of deuterium, an isotope of hydrogen whose nucleus holds one proton and one neutron. The contrast could not be more stark: Low-mass M-class stars can burn hydrogen for tens of billions of years, with longevity far beyond that of our Sun. Brown dwarfs keep getting cooler after going through a short period of deuterium burning. The problem is that only about 30 brown dwarfs have been accurately characterized, as University of Geneva researcher Nolan Grieves points out.
“…we still do not know exactly where the mass limits of brown dwarfs lie, limits that allow them to be distinguished from low-mass stars that can burn hydrogen for many billions of years, whereas a brown dwarf will have a short burning stage and then a colder life. These limits vary depending on the chemical composition of the brown dwarf, for example, or the way it formed, as well as its initial radius.”
The scholarship on brown dwarf mass generally sets a limit of 13 Jupiter masses (MJup) as the dividing line between a gas giant and a brown dwarf. This is the approximate mass that an object must reach to ignite deuterium fusion in its core. The upper limit, dividing brown dwarf from star, has been commonly set at 80 Jupiter masses, which is where the object is massive enough to begin hydrogen burning, fusing hydrogen nuclei into helium nuclei. Exactly where these boundaries occur, though, depends on the chemical composition of the particular object in question.
Thus the value of the work Grieves and team have produced, a study of five brown dwarfs that were found in TESS data through their transit signature and later analyzed using radial velocity methods. They are ‘companion’ objects, as opposed to unbound brown dwarfs. All are near the hydrogen-burning mass limit. Their main sequence host stars were originally identified as TESS Objects of Interest (TOI), and the companions orbit with periods ranging between 5 and 27 days. Because they transit, we can also detect their radii, between 0.81 and 1.66 times Jupiter’s radius. They range in mass between 77 and 98 Jupiter masses, which nudges them into M-dwarf territory.
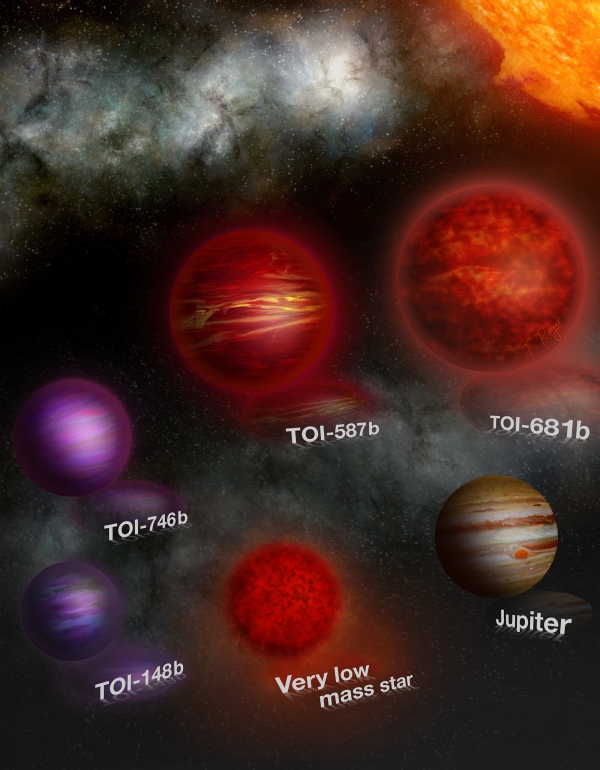
Image: This artist’s illustration represents the five brown dwarfs discovered with the satellite TESS. These objects are all in close orbits of 5-27 days (at least 3 times closer than Mercury is to the Sun) around their much larger host stars. Credit: CC BY-NC-SA 4.0 – Thibaut Roger – UNIGE.
Are we sure these detections are not of very low mass stars? One way of approaching the matter is to look at the relationship between their size and age. A brown dwarf will lose deuterium as it burns up its reserves, thus cooling down and shrinking over time. The fact that the two oldest TESS Objects of Interest — TOI 148 and TOI 746 — have smaller radii while the younger objects are larger points to the likelihood that the former are brown dwarfs.
These age estimates are based, in the case of the comparatively young TOI-587, on what is known as ‘isochrone stellar modelling,’ which essentially fits data onto the Hertzsprung-Russell diagram to draw conclusions about the ages of stars in clusters. The young age of TOI-681 is likewise drawn from inferences due to its membership in a cluster. But even these rough estimates are compromised by the fact that TOI-681b makes only a grazing transit, as does another of the TESS finds, TOI-1213b.
I mention the age issue as just one factor in working out the nature of these objects, and one that is itself not well constrained. Given the uncertainties, the authors’ conclusion points to the need to compile a larger dataset for brown dwarfs:
The sample of transiting brown dwarfs and low-mass stars we analyzed is still too small to make significant statistical claims; however, their eccentricity and metallicity distributions are still consistent with previous suggestions of two separate populations for lower and higher mass brown dwarfs. These companions are all near the hydrogen-burning mass limit and add to the statistical sample needed to distinguish the population differences between brown dwarfs and low-mass stars.
Note that comment on two separate populations of brown dwarfs depending upon mass. We’re just getting a handle on these issues. The questions that hovered over my post-dinner conversation on brown dwarfs back in the 1990s continue to vex astronomers as we probe this class. Defining separate populations for these objects seems to be where we’re headed as we craft formation models.
Bear this in mind: Brown dwarfs rarely occur in close orbits around main sequence stars, the word ‘close’ in this case meaning orbits at 5 AU or closer to the primary. Thus the phrase ‘brown dwarf desert’ to characterize orbits that brown dwarfs rarely occupy as a companion object. The authors think this lack of brown dwarf companions relates to formation mechanisms, though the jury is out:
The relative lack of brown dwarf companions may be related to a transition of the formation mechanisms required to form giant planets and low-mass stars. In this case, lower mass brown dwarfs may form similar to giant planets via core accretion (Pollack et al. 1996) or disk instability (Cameron 1978; Boss 1997) and higher mass brown dwarfs may form similar to stars from gravitational collapse and turbulent fragmentation of molecular clouds (Padoan & Nordlund 2004; Hennebelle & Chabrier 2008). The boundary of these formation mechanisms is unclear and certainly depends on an object’s initial environment.
Brown dwarfs that can be well characterized are the key to resolving these issues, especially those whose radius can be precisely determined, as in the new TESS discoveries. Here we have the kind of robust photometric and spectroscopic measurements that will help astronomers test current formation models.
The paper is Grieves et al., “Populating the brown dwarf and stellar boundary: Five stars with transiting companions near the hydrogen-burning mass limit, Astronomy & Astrophysics Vol. 652, A127 (August, 2021). Abstract / Preprint.



Since all star systems must form through angular momentum, the same must be true about brown dwarf stars which must experience gravitational collapse. The largest body will experience the collapse at the center of a molecular cloud. Most of the mass is also in binary systems which would also have to have gravitational collapse.. It would be interesting to see if brown dwarfs 7 to 20 AU apart have any planets since the same physics must apply to stars, the angular momentum in such systems would be used up and none would be left for planets according to Kippenhahn’s idea, 1983.
A question about the core densities of stars and planets:
From the internet, I get these rough estimates of the density of these bodies’ cores:
Name density (g.cm^3)
Sun 162
M Dwarf 500
Brown dwarf 10-1000
Jupiter 12
Earth 10-12
IDK enough about the different fusion processes in stars, but it seems as though M dwarfs must be denser than the sun to ensure slow, continued fusion.
Jupiter has a much lower density (rocky/metallic hydrogen[?] core, comparable to earth’s iron core in density.
In between the brown dwarfs seem to have cores that have a density range of 2 orders of magnitude. Is it at the high end (1000 g/cm^3) that they may sustain deuterium fusion for a while? When fusion stops or their mass is lower, is the density at the lower level more comparable to that of Jupiter?
But from the text:
I usually associate shrinking with becoming denser, yet if I have the core density argument correct, then the star’s density decreases suggesting it must expand – or at least the core expands while the rest of the star’s mass could increase in density. The average densities of our sun and Jupiter are comparable, 1.4 vs 1.33 g/cm^3 which suggests that is where a brown dwarf’s density should be too.
Without too much detail, can someone enlighten me as to the issue of core density and nuclear fusion in G, M, and brown dwarf stars, and/or point me to a good popsci article that explains this well?
When a planet reaches a little less than the size of Jupiter, it begins to accumulate some “metallic hydrogen” at the center. Metallic hydrogen seems to be more or less equivalent to electron degenerate matter; it is a sea of hydrogen nuclei and electrons, with the electrons held apart by the Pauli exclusion principle. (In white dwarfs there is electron degenerate matter with more carbon nuclei) The effect is that once a planet grows to the radius of Jupiter, it doesn’t get bigger if you dump more material into it. *Until* 80 Jupiter masses or so, when it becomes a sufficiently active star to make itself expand again. So between the Sun and Jupiter there is, yes, a large range of vastly denser objects, many of which are about the same size as Jupiter. If I recall correctly, white dwarfs are a bit smaller because their carbon nuclei are half neutrons, so they have twice the nuclear mass per electron; also, they can’t stably undergo fusion no matter how big they are, and they must collapse further or have a type Ia supernova if more mass is added.
A.T.,
In the discussion above, you note that high mass and density brown dwarfs do engage in deuterium fusion. So, up around the 80 jovian
mass for sure. But intrinsic in the definition of brown dwarfs is the idea that they start at a lower value: 13 jovian masses. Then they use it all up and continue their lives with varying stores of internal heat. The fusion period over the mass range is short. An early
estimate that sticks in my head is 300,000 years. And I suspect it was from an article in a decades back ASU collection of survey articles. But it stands to reason that that value does not cover the range of masses.
Jupiters and brown dwarfs share roughly the same dimensions, but I suspect they bulge with increased internal temperatures, retained heat from formation and their deuterium sagas.
There has got to be some more detailed models of these life histories
somewhere. Maybe even extremely red portions of the HZ diagram
showing traces for various mass BDs.
That’s a really great explanation, Mike Serfas, I finally have a mental model of why high mass planets and brown dwarf’s are similar in size.
A smaller percentage of Jupiter’s core is very dense metallic hydrogen vs a brown dwarf, and at some point as mass is added…. it destabilizes this phase and the object grows in diameter.
It appears that I am already wrong about part of it, based on this report about white dwarfs and stable fusion: https://phys.org/news/2021-09-hubble-hydrogen-burning-white-dwarfs-aging.html But I didn’t find it on Arxiv.
Alex Tolley, the pressure needed for fusion in the smallest stars or M dwarfs is much higher than in gas giants and planets. The core temperature is always based on mass which uses the principle of general relativity. The higher the mass, the greater the core temperature and pressure. For example: The core temperature of Uranus is 5ooo K at 8Mbar or 8 million bars, one bar is the pressure of one Earth atmosphere. Jupiter 70 Mbar at at 17, 000 K. Brown dwarf Gliese 229B has a core temperature 500,000 K at 170 gegabar Gbar or 170 billion bars. The core pressure and temperature of our Sun is 250 billion atmospheres or 250Gbar at 15 million kelvin or 27 million F. The New Solar System. p. 197 and google. Once the mass is more than 80 Jupiter masses and the core temperature reaches 10 million kelvin, fusion begins. The particles in the center move and collide with each other and the more the mass. the stronger the gravity at the core, and the faster they collide which makes the high temperature. The speed of particle collisions in the center of our Sun is 500 km per second.
I was thinking that before there can be accretion there has to be first angular momentum so brown dwarfs have high mass so they all most likely form from a gravitational collapse, but maybe there is some accretion also, but accretion has only a flat orbit at a certain distance to get gas and dust, but not collapse which is from every direction.
One problem with any models for stellar fusion is the high magnetic fields that are generated as these objects become smaller. The suns 22 year cycle is still not well understood and the pattern that the sunspots form over that cycle is a mystery. I believe we still have much to learn and these patterns may be related to a magnetic and quantum wave structures that are created deep in the sun and other stars.
Well it just got a lot weirder;
An Accidental Discovery Hints at a Hidden Population of Cosmic Objects.
https://www.jpl.nasa.gov/news/an-accidental-discovery-hints-at-a-hidden-population-of-cosmic-objects
Where we one the subject this is interesting
An Accidental Discovery Hints at a Hidden Population of Cosmic Objects
https://www.jpl.nasa.gov/news/an-accidental-discovery-hints-at-a-hidden-population-of-cosmic-objects