Just how likely is it that the galaxy is filled with technological civilizations? Kelvin F Long takes a look at the question using diffusion equations to probe the possible interactions among interstellar civilizations. Kelvin is an aerospace engineer, physicist and author of Deep Space Propulsion: A Roadmap to Interstellar Flight (Springer, 2011). He is the Director of the Interstellar Research Centre (UK), has been on the advisory committee of Breakthrough Starshot since its inception in 2016, and was the co-founder of Icarus Interstellar and the Initiative/Institute for Interstellar Studies, He has served as editor of the Journal of the British Interplanetary Society and continues to maintain the Interstellar Studies Bibliography, currently listing some 1400 papers on the subject.
by Kelvin F Long

Many excellent papers have been written about the Fermi paradox over the years, and until we find solid evidence for the existence of life or intelligent life elsewhere in the galaxy the best we can do is to estimate based on what we do know about the nature of the world we live in and the surrounding universe we observe across space and time.
Yet ultimately to increase the chances of finding life we need to send robotic probes external to our solar system to visit the planets around other stars. Whilst telescopes can do a lot of significant science, in principle a probe can conduct in-situ reconnaissance of the system to include orbiters, atmospheric penetrators and even landers.
Currently, the Voyager 1 and 2 probes are taking up the vanguard of this frontier and hopefully in the years ahead more will follow in their wake. Although these are only planetary flyby probes and would take tens of thousands of years to reach the nearest stars, our toes have been dipped into the cosmic ocean at least, and this is a start.
If we can send a probe out into the Cosmos, it stands to reason that other civilizations may do the same. As probes from different civilizations explore space, there is a possibility that they may encounter each other. Indeed, it could be argued that the probability of species-species first contact is more with their robotic ambassadors rather than the original biological organisms that launched them on their vast journeys.
However, the actual probability of two different probes from alternative points of origin (different species) interacting is low. This is for several reasons. The first relates to astrobiology in that we do not yet know how frequent life is in the galaxy. The second relates to the time of departure of the probes within the galaxy’s history. Two probes may appear in the same region of space, but if this happens millions of years apart then they will not meet. Third, and an issue not often discussed in the literature, is the fact that each probe will have a different propulsion system and so its velocity of motion will be different.
As a result, not only do probes have to contend with relativistic effects with respect to their world of origin (particularly if they are going close to the speed of light), but they will also have to deal with the fact that their clocks are not synchronised with each other. The implication is that for probes interacting from civilizations that are far apart, the relativistic effects become so large that it creates a complex scenario of temporal synchronization. This becomes more pronounced the larger the different species of probes, and the larger the difference in the respective average speeds. This is a state we might call ‘temporal spaghettification’, in reference to the complex space-time history of the spacecraft trajectories relative to each other.
An implication of this is that ideas like the Isaac Asimov Foundation series, where vast empires are constructed across hundreds or thousands of light years of space, do not seem plausible. This is particularly the case for ultra-fast speeds (where relativistic effects dominate) that do approach the speed of light. In general, the faster the probe speeds and the further apart the separate civilizations, the more pronounced the effect. In 2016 this author framed the idea as a postulate:
“Ultra-relativistic spaceflight leads to temporal spaghettification and is not compatible with galaxy wide civilizations interacting in stable equilibrium.”
Another consequence of ultra-fast speeds is that if civilizations do interact, it will not be possible to prevent the technology (i.e. power and propulsion) associated with the more advanced race from eventually emerging within the other species at some point in the future. Imagine, for example, if a species turned up with faster than light drives and simply chose to share that technology, even if for a price, as a part of a cultural information exchange.
Should such a culture refuse to share that technology with us, we would likely work towards its fruition anyway. This is because our knowledge of its existence will promote research within our own science to work towards its realisation. Alternatively, knowledge of that technology will eventually just leak out and be known by others.
There is also a statistical probability that if it can be invented by one species, it will be invented by another; as a law of large numbers. As a result when one species has this technology and starts interacting with others, eventually many other species will obtain it, even if it takes a long time to mature. We might think of this as a form of technological equilibration, in reference to an analogy to thermodynamics.
Ultimately, this implies that it is not possible to contain the information associated with the technology forever once species-species interaction begins. Indeed, it has been discovered that even the gravitational prisons of light (black holes) are leaky through Hawking evaporation. The idea that there is no such thing as a permanently closed system was also previously framed as a second postulate by this author:
“No information can be contained in any system indefinitely.”
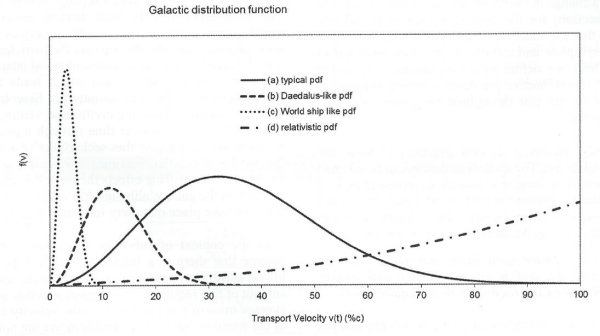
Adopting analogues from plasma physics and the concept of distribution functions, we can imagine a scenario in which within a galaxy there are multiple populations, each sending out waves of probes at some average velocity of expansion rate. If most of the populations adopted fusion propulsion technology, for example, as their choice of interstellar transport, then the average velocity might be around 0.1c (i.e. plausible speeds for fusion propulsion are 0.05-0.15c) and this would then define the peak of a velocity distribution function.
The case of human-carrying ships may be represented by world ships traveling at the slow speeds of 0.01-0.03c. In the scenario of the majority of the populations employing a more energetic propulsion method, such as using antimatter fuel, the peak would shift to the right. In general, the faster the average expansion speed, the further to the right the peak would shift, since the peak represents the average velocity.
The more the populations interacted, the greater the technological equilibration over time, and this could see a gradual shift into the relativistic and then ultra-relativistic (>0.9c) speed regimes. Yet, due to the limiting factor of the speed of light limit (~300,000 km/s or 1c), the peak would start to move asymptotically towards some infinite value.
There is also the special case of faster-than-light travel (ftl), but by the second postulate if any one civilization develops it then eventually many of the others will also develop it. Then as the mean velocity of many of the galactic populations tends towards some ftl value, you get a situation where many civilizations can now leave the galaxy, creating a massive population expansion outwards, as starships are essentially capable of reaching other galaxies. That population would also be expanding inwards to the other stars within our galaxy since trip times are so short. Indeed, ships would also be arriving from other galaxies due to the ease of travel. But if this were the case, starships would be arriving in Earth orbit by now.
In effect, the more those civilizations interact, the more the average speed of spacecraft in the galaxy would shift to higher speeds, and eventually this average would begin to move asymptotically towards ftl (assuming it is physically possible), which is an effect we might refer to as ‘spatial runaway’ since there is no longer any tendency towards some equilibrium speed limit. In addition, the ubiquity of ftl transport comes with all sorts of implications for communications and causality and in general creates a chaotic scenario that does not lean towards a stable state.
This then leads to the third postulate:
“Faster than light spaceflight leads to spatial runaway, and is not compatible with galaxy wide civilizations interacting in stable equilibrium.”
Each species that is closely interacting may start out with different propulsion systems so that they have an average speed of population expansion, but if technology is swapped there will be some sort of equilibration that will occur such that all species tend towards some mean velocity of population diffusion.
The modeling of a population density of a substance is borrowed from stochastic potential theory, with discrete implementation for the quantization of space and time intervals by the use of average collision parameters. This is analogous to problems such as Brownian motion, where particles undergo a random walk. This can be adopted as an analogy to explain the motion of a population of interstellar probes dispersing through the galaxy from a point of origin.
Modeling population interaction is best done using the diffusion equation of physics, which is derived from Fick’s first and second law for the dispersion of a material flux, and also the continuity equation. This is a second order partial differential equation and its solution for a population that starts with some initial high density and drops to some low density. It is given by a flux equation which is a function of both distance and time. This equation is proportional to the exponential of the negative distance squared.
Using this physics as a model, it is possible to show that the galaxy can be populated within only a couple of million years, but even faster if the population is growing rapidly, as for instance via von Neumann self-replication. A key part of the use of the diffusion equation is the definition of a diffusion coefficient which is equal to ½(distance squared/time), where the distance is the average collision distance between stars (assumed to be around 5 light years) and time is the average collision time between stars (assumed to be between 50-100 years for 0.05-0.1c average speed). These relatively low cruise speeds were chosen because the calculations were conducted in relation to fusion propulsion designs only.
For probes that eventually manufacture another probe on average (i.e., not fully self-reproducing), this might be seen as analogous to a critical nuclear state. Where the probe reproduction rate drops to less than unity on average, this is like a sub-critical state and eventually the probe population will fall-off until some stagnation horizon is reached. For example, calculations by this author using the diffusion equation show that with an initial population as large as 1 million probes, each traveling at an average velocity of 0.1c, after about ~1,000 years the population would have stagnated at a distance of approximately ~100 light years.
If however, the number of probes being produced is greater than unity, such as through self-replicating von Neumann probes, then the population will grow from a low density state to a high density state as a type of geometrical progression. This is analogous to a supercritical state. For example, if each probe produced a further two probes on average from a starting population of 10 probes, then by the 10th generation there would be a total of 10,000 probes in the population.
Assume that there are at least 100 billion stars in the Milky Way galaxy. For the number of von Neumann probes in the population to equal that number of stars would only require a starting population of less than 100 probe factories, with each producing 10 replication probes, and after only 10 generations of replication. This underscores the argument made by some such as Boyce (Extraterrestrial Encounter, A Personal Perspective, 1979) that von Neumann-like replication probes should be here already. The suggestion of self-replicating probes was advanced by Bracewell (The Galactic Club: Intelligent Life in Outer Space, 1975) but has its origins in automata replication and the research of John von Neumann (Theory of Self-Reproducing Automata, 1966).
Any discussion about robotic probes interacting is also a discussion about the number of intelligent civilizations – such probes had to be originally designed by someone. It is possible that these probes are no longer in contact with their originator civilization, which may be many hundreds of light years away. This is why such probes would have to be fully autonomous in their decision making capability. Indeed, it could be argued that the probability of the human species first meeting an artificial intelligence-based robotic probe is more likely than meeting an alien biological organism. It may also be the case that in reality there is no difference, if biological entities have figured out how to go fully artificial and avoid their mortal fate.
Indeed, when considering the future of Homo Sapiens and our continued convergence with technology the science and science fiction writer Arthur C Clarke referred to a new species that would eventually emerge, which he called Homo Electronicus. He depicted it thus:
“One day we may be able to enter into temporary unions with any sufficiently sophisticated machines, thus being able not merely to control but to become a spaceship or a submarine or a TV network….the thrill that can be obtained from driving a racing car or flying an aeroplane may be only a pale ghost of the excitement our great grandchildren may know, when the individual human consciousness is free to roam at will from machines to machine, through all reaches of sea and sky and space.” (Profiles of the Future, 1962).
So even the idea of separating a biological organism from a machine intelligence may be an incorrect description of the likely encounter scenarios of the future. A von Neumann robotic spacecraft could turn up in our orbit tomorrow and from a cultural information exchange perspective there may be no distinction. It is certainly the case that robotic probes are more suited for the environment of space than biological organisms that require a survival environment.
Consider a thought experiment. Assume the galaxy’s disc diameter is 100,000 light years and consider only one dimension of space. A population of probes starts out at one end with an average diffusion wave speed of around 10 percent of the speed of light (0.1c). We assume no stopping and instantaneous time between populations of diffusion waves (in reality, there would be a superposition of diffusion waves propagating as a function of distance and time). This diffusion wave would take on the order of 1 million years to cross from one side of the galaxy to the other. We can continue this thought experiment and imagine that the same population starts at the centre and expands out as a spherical diffusion wave. Assuming that the wave did not dissipate and continued to grow, then the time to cover the galactic disc would be approximately half than if it had started on one side.
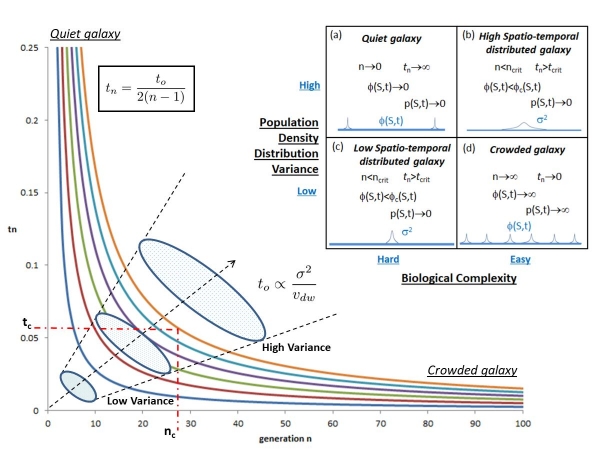
Now imagine there are two originating civilizations, each sending out populations of probes that continue to grow and do not dissipate. These two civilizations are located at opposite ends of the galaxy. The time for the galaxy to be covered by the two populations will now be half of a single population starting out on the edge of the disc. We can continue to add more numbers of populations n=1,2,3,4,5,6….and we get t, t/2, t/4, t/6, t/8, t/10…and we eventually find that for n>1 it follows a geometrical series of the form tn=t0/2(n-1), where t0 is the galactic crossing timescale (i.e. 1 million years) assumed for an initiating population of probes derived from a single civilization which is a function of the diffusion wave speed.
So that for a high number of initiating populations where n ? infinity, the interaction time between populations will be low so that tn ? 0, and the probability of interaction is therefore high. However, for a low number of initiating populations where n ? 0, the interaction time between populations will be high, so that tn ? infinity; thus the timescales between potential interactions are a lot larger and the probability of interaction is therefore low.
It is important to clarify the definition of interaction time used here. The shorter the interaction time, the higher the probability of interaction, since the time between effective overlapping diffusion waves is short. Conversely, where the interaction time is long, the time between overlapping diffusion waves is long and so the probability of interaction is low. The illustrated graphic below demonstrates these limits and the boxes are the results of diffusion calculations and the implications for population interaction.
As discussed by Bond & Martin (‘Is Mankind Unique?’, JBIS 36, 1983), the graphic illustrates two extreme viewpoints about intelligence within the galaxy. The first is known as Drake-Sagan chauvinism and advocates for a crowded galaxy. This has been argued by Shklovskii & Sagan (‘Intelligent Life in the Universe’, 1966), Sagan & Drake (The Search for Extraterrestrial Intelligence, 1975). In the graphic this occurs when n ? ? , tn ? 0, so that the probability of interaction is extremely high.
Especially since there are likely to be a large superposition of diffusion waves overlapping each other. This effect would become more pronounced for multiple populations of vN probes diffusing simultaneously. We note also that an implication of this model for the galaxy is that if there are large populations of probes, then there must have been large populations of civilizations to launch them, which implies that the many steps to complexity in astrobiology are easier than we might believe. In terms of diffusion waves this scenario is characterised by very high population densities such that ?(S,t) ? ? which also implies that the probability of probe-probe interaction is high p(S,t) ? ?. This is box (d) in the graphic.
The second viewpoint is known as Hart-Viewing chauvinism and advocates for a quiet galaxy. This has been argued by Tipler (‘Extraterrestrial Intelligent Beings do not Exist’, 1980), Hart (‘An Explanation for the Absence of Extraterrestrials on Earth’, 1975) and Viewing (‘Directly Interacting Extraterrestrial Technological Communities’, 1975). This occurs when n ? 0, tn ? ?, so that the probability of interaction is extremely low. In contrast with the first argument, this might imply that the many steps to complexity in astrobiology are hard. This scenario is characterised by very low population densities such that ?(S,t) ? 0 so that few diffusion waves can be expected and also that the probability of interaction is low p(S,t) ? 0. This is box (a) in the graphic.
In discussing biological complexity, we are referring to the difficulty in going from single celled to multi-celled organisms, but then also to large animals, and then to intelligent life which proceeds towards a state of advanced technological attainment. A state where biology is considered ‘easy’ is when all this happens regularly provided the environmental conditions for life are met within a habitat. A state where biology is considered ‘hard’ may be, for example, where it may be possible for life to emerge purely as a function of chemistry but building that up to more complex life such as to an intelligent life-form that may one day build robotic probes is a lot more difficult and less probable. This is a reference to the science of astrobiology which will not be discussed further here. However, since the existence of robotic probes would require a starting population of organisms it has to be mentioned at least.
Given that these two extremes are the limits of our argument, it stands to reason that there must be transition regimes in between which either work towards or against the existence of intelligence and therefore the probability of interaction. The right set of parameters would be optimum to explain our own thinking around the Fermi paradox in terms of our theoretical predictions being in contradiction to our observations.
As shown in the graphic it comes down to the variance ?2 of the statistical distribution for the distance S of a number of probe populations ni within a region of space in a galaxy (not necessarily a whole galaxy), where the variance is also the square root of the standard distribution ? relative to a mean distance between population sources ?S. In other words whether the originating civilizations that initiated the probe populations are closely compacted or widely spread out.
A region of space which had a high probe population density (not spread out or sharp distribution function) would be characterised by a low variance. A region with a low probe population density (widely distributed or flattened distribution function) would be characterised by a high variance. The starting interaction time to of two separate diffusion waves from independent civilizations would then be proportional to the variance and the diffusion wave velocity vdw of each population such that to is proportional to ?2/vdw.
Going back to the graphic there comes a point where the number of populations of probes becomes less than some critical number n<nc, the value of which we do not know, but as this threshold is crossed the interaction time will also increase past that critical value tn>tc. In box (c) of the graphic, biology is ‘hard’ and so despite the low variance the population density will be less than some critical value ?(S,t)<?c(S,t) which means that the probability of probe-probe interaction will be low p(S,t) ? 0. This is referred to as a low spatio-temporal distributed galaxy. Whereas for box (b) of the graphic although biology may be ‘easy’, the large variance of the populations makes for a low population density of the total combined and so also a low probability of probe-probe interaction. This is referred to as a high spatio-temporal distributed galaxy.
Taking all this into account and assessing the Milky Way, we don’t see evidence of a crowded galaxy, which would rule out box (d) in the graphic. In this author’s opinion the existence of life on Earth and its diversity does not imply (at least) consistency with a quiet galaxy (unless one is invoking something special about planet Earth). This is indicated in (a). On the basis of all this, we might consider a fourth postulate along the following lines:
“The probability of interaction for advanced technological intelligent civilizations within a galaxy strongly depends on the number of such civilizations, and their spatial-temporal variance.”
Due to the exponential fall-off in the solution of the diffusion wave equation, the various calculations by this author suggest that intelligent life may occur at distances of less than ~200 ly, which for a 100-200 kly diameter galaxy might suggest somewhere in the range of ~500-1,000 intelligent civilizations along a galactic disc. Given the vast numbers of stars in the galaxy this would lean towards a sparsely populated galaxy, but one where civilizations do occur. Then considering the calculated time scales for interaction, the high probability of von Neumann probes or other types of probes interacting therefore remains.
We note that the actual diffusion calculations performed by this author showed that even with a seed population of 1 billion probes, the distance where the population falls off was at around ~164 ly. This is not too dissimilar to the independent conclusion of Betinis (“On ETI Alien Probe Flux Density”, JBIS, 1978) who calculated that the sources of probes would likely be somewhere within 70-140 ly. Bond and Martin (‘A Conservative Estimate of the Number of Habitable Planets in the Galaxy’ 1978) also calculated that the average distance between habitable planets was likely ~110 ly and ~140 ly between intelligent life relevant planets. Sagan (‘Direct Contact Among Galactic Civilizations by Relativistic Interstellar Spaceflight’, 1963) also calculated that the most probable distance to the nearest extant advanced technical civilization in our galaxy would be several hundred light years. This all implies that an extraterrestrial civilization would be at less than several hundred light years distance, and this therefore is where we should focus search efforts.
When it comes down to the Fermi paradox, this analysis implies that we live in a moderately populated galaxy, and so the probability of interaction is low when considering both the spatial and temporal scales. However, when it comes to von Neumann probes it is clear that the galaxy could potentially be populated in a timescale of less than a million years. This implies they should be here already. As we perhaps ponder recent news stories that are gaining popular attention, we might once again consider the words of Arthur C Clarke in this regard:
“I can never look now at the Milky Way without wondering from which of those banked clouds of stars the emissaries are coming…I do not think we will have to wait for long.” (‘The Sentinel’, 1951).
The content of this article is by this author and appears in a recently accepted 2022 paper for the Journal of the British Interplanetary Society titled ‘Galactic Crossing Times for Robotic Probes Driven by Inertial Confinement Fusion Propulsion’, as well as in an earlier paper published in the same journal titled ‘Unstable Equilibrium Hypothesis: A Consideration of Ultra-Relativistic and Faster than Light Interstellar Spaceflight’, JBIS, 69, 2016.



You are making an assumption that once technological intelligence occurs, it continues to develop and become at least probe-producing, if not space-faring. This may not be true. It is possible that species that become technologically very capable inevitably make mistakes and wipe themselves out, never to recover a strong technological civilization again. The galaxy could be littered with living worlds, but only the geological/archaeological evidence of such civilizations. While it has been argued that only one civilization needs to avoid that fate, that assumption may not be true for reasons as yet unclear.
If we live in a moderately populated galaxy, then so far there is no evidence of it from what we might expect from a technological civilization. They may not send out probes, but there is as yet no indication of other technological artifacts of a technological civilization. Certainly, we may not recognize the signs, but soon we will have evidence of biosignatures and the question will then arise, why is there no associated technological civilization – extant or even extinct?
If vN probes are already in the galaxy, we must be rather unlucky to live in a time when they have not quite reached us and make it appear the galaxy is empty. Had we become technologically capable, say after another 300,000 years, would we look up and see signs of vN probes all around us?
If the galaxy does have many, but apparently hidden/hiding civilizations, then the vN probe argument however refined, fails to explain the Fermi Paradox. If, as the previous post intimates, we are close to building vN-type replicators (which I agree with) then it seems reasonable to suggest that due to the spatio-temporal distributions of civilizations, they should be here now. In a million years, if we have launched ours before our possible demise, other civilizations, if there are any, will not fail to see evidence of their prior or current presence in their systems.
Sorry, Kelvin, I can’t follow your reasoning at all. So far as I can see, you’ve assumed that alien industrial civilisations exist in the Galaxy, and from that you’ve concluded that they exist. Clearly I must have missed something, so maybe another reader of this blog can explain it to me?
I wonder what proportion of civilisations you are assuming to be one-planet, zero-growth ones, and what proportion multi-planet, positive-growth ones? (See JBIS, Nov. 2021, p.401-402.)
Stephen
Studies like this would benefit from a cost-benefit analysis, even if necessarily somewhat fanciful. We know there are costs, if poorly quantified, but what is the benefit of propagation? Does the benefit exceed the cost?
The cost includes risk. Establishing a colony of the same biological heritage and culture is a colony that will turn right back at its origin since they would have similar objectives, such as the resources they covet and philosophical imperatives. Conflict can result.
Meeting another propagator, machine or biological, also entails risk. Maybe they’ll coexist and be good neighbors. They might also conflict, with risk to one or more of the propagators. It would not be difficult to follow the trail back to their origin.
The benefit of propagation would have to be substantial to entail the known and unknown risks. Otherwise the propagation will need to proceed with extraordinary care, avoiding others, obscuring their own history/origin, and only observing at a safe distance when encountering others.
Without an understanding of the costs and benefits, any strategy, no matter how feasible, is merely fanciful.
Alex Tolley: Yes, arguably, there is another category aligned with biology hard/easy, which is technology hard/easy; although this is sort of implied in the limit of biology easy as the end point of a species evolution. However, statistically speaking, if you have a quantity of civilizations that become technologically mature, it only requires a small fraction of those to succeed to space probe level which would eventually lead to galactic population seeding; especially if any of them develops vN probes. You could have a 99% failure rate due to technological/environmental destruction, but that 1% may still be a significant quantity.
By moderately populated galaxy, I meant over the galaxies history. For example the 5,000-10,000 civilizations along the galactic disc I estimated, may be over say 5 billion years rather than simultaneously. Hence the probability of interaction is low. But on vN probes, just because it’s an opinion they are not seen it doesn’t mean they are not here. This is a question of what observations we are prepared to accept and how we interpret them which I think is fundamental.
Stephen: Sort of, I have looked at the conclusions of making that assumption in terms of its implication. In regards to the proportion, no assumption made, but I examined the extremes of this in my paper, in terms of a quiet galaxy to a crowded galaxy.
Ron S: I think it depends on the purpose of the probe. In my paper I defined several types. Overall, this comes down to the philosophy of the culture that originates the probes and what drives them.
OT but what happened to Project Icarus? The web has been down for several years now.
@Kelvin Long
Thank you for your nice replies here.
The main caveat to any discussion about extraterrestrial life is that we simply do not know how and exactly under which conditions life got started in the first place. And unless there’s other types of chemistries, genetic coding, antibodies and whatever set of characteristics we got on Earth. Life itself might be rather rare.
But once it gotten started, as a biologist I must however there’s no such thing as an ‘end point’ to a species evolution. Neither is there’s a built in plan for where evolution is supposed to lead – such as a lifeforms with advanced neural systems who also are tool users that eventually could become technological.
The make-or-break as a selector is if the characteristic guarantee that the offspring carry the genetic material to the next generation. Such a selection could lead to endless types of ecologies where advanced life never occurs. This from the simple example of fast breeding photosynthetic prokaryotes that simply outcompete all other types of plant life. To insect (or any analogous species) worlds where ubiquitous species of insects -lets say aggressive ants- prevent the development of species that got an advanced brain. On such worlds the evolution between the competing species might lead to amazing specialization over time – perhaps even tools used as weapons – but without any intelligence and only guided by inborn instinct.
But even that speculation is limited by using Earth based examples. There might be many others. Some already covered in Science fiction.
As for the 5 billion year span, I do agree.
Even I do think that once in a while a technological civ will appear, but the chance that we would have turned up at the same time as another technological species is alive and active close enough on the galactic stage that we would interact is quite unlikely.
If the final confirmation that we’re not the only species that have developed to a technological species is a signal, its most likely from one who’s already gone. And that species even more likely to be extinct if that confirmation comes in the form of an artefact, since physical travel have to be slower than light or radio.
https://arxiv.org/abs/1802.09399v1
I like the idea that ET’s with warp drives might give that technology to us because I would like to see the dinosaur planet or the anti gravity car. I don’t think that will happen because we are still barbarians who have wars with each other. Also there is probably an ethics that ET”s with advanced technology have that every planet must develop their own faster than light interstellar travel because if they helped us, it would be cheating us out of thinking for ourselves and the feeling of new discoveries and of how to do it for ourselves which Albert Einstein thought was important.
The problem with the Fermi Paradox is that it is too easy to get stuck in thinking about ET’s which is trapped in the past or does not go beyond today’s level of technology which is what works today. There can be more than one explanation of why we have not been contacted by any ET’s: Ethical reasons are one of them which Carl Sagan wrote about in Cosmos, Encyclopedia Galactica. It seems to me that any ET civilization with a warp drive would not need to communicate with us and if they did not want to do that, there would be no way we could know that they are there with our primitive technology. If those UAP’s can disappear from our radar, then so can a starship with a warp drive. We could never know if it was in orbit or anywhere else in our solar system. If we could build a battleship size object with stealth technology, then they certainly could. I recall an episode of Star Trek the original series the enterprise accidentally went back in time where their deflector shield made the USS Enterprise invisible to radar.
We are also completely radio silent due to inverse square law of electromagnetic radiation or radio signals. Our powerfullest radio station is only 50,000 watts of power. I would take a radio signal with one million watts of power just to get to the nears star at 4.3 lightyears. At one lightyear, for that past one hundred years you would not have heard anything since any radio signals of radio stations of the past won’t make it even one light year. A civilization with our level of advancement which is one thousand light years away does not even know we are here. What if most of the civilizations in our galaxy has FTL? That would explain why we have not heard anything. We are not part of the galactic club which does not need self replicating machines to exist. It could also come on go quickly stay for a couple of weeks and leave taking it’s spy probes with it without needing to leave anything behind or any trace. This is only a speculation, but it is easy to conclude that if one has negative energy, anti gravity spy probes, then one has a negative energy faster than light warp drive which works on the same principle. These ideas are so cutting edge and the technology so much more advanced than ours it is easy to assume it is just impossible, dismiss the UAP’s and stick to our own level of technology to understand something.
My observations of UAP’s got me interested in warp drives and FTL technology and also NASA’s Breakthrough Propulsion Physics Program and the book Frontiers of Propulsion Science.
In my mind we have already crossed a threshold in that we went from faster than light travel was absolutely impossible to faster than light travel is at least theoretically possible. Given our historic rate of technological development that might be enough for an advanced species to decide to share what they have.
I didn’t know there was a term for it (“technological equilibration”) and I was thinking of nations here on Earth rather than intelligent species on other planets, but it occurred to me a little while ago that any advantage a country derived from a technological or even a larger cultural innovation was likely to be temporary. The dominance of Britain (first to industrialize) faded, and that of the U.S. (only undamaged industrial nation after WW2) appears to be also. We may be returning to a pre-1700 world with a number of more or less equally powerful regional civilizations.
Yes, a possible return to a multi-polar world. I am old enough to have read President Carter’s report on the World in 2000. It predicted such a world, but instead we got a triumphal unipolar world. That period appears to be ending, and the US may be in decline faster than expected even just a decade ago.
A long article which I will have to read more carefully later.
Two points:
1. The ruins of a device can still tell us much, such as that ancient astronomical computer found in a Greek shipwreck, or the rusted remains of a buried auto to be found in a few thousand years.
Ruins? I read that the Pioneer and Voyager probes are being eroded by stray atoms hitting them, about 10 angstroms (1 nanometer) a year. In 500,000 years, the paint will be gone, and in a billion years, nothing will be left.
Consider a probe lurking near the James Web Telescope, exposed to the solar wind and micrometeors. Maybe the radio dish and a couple of arms holding instruments are missing, but the remains of the main body, such as the engine, could still tell us much, IF we can spot the probe in the first place. What next? Then the Pentagon would lasso the probe and bring it to Area 51 for disassembly, without China suspecting a thing – no way!
2. Technology transfer: an analogy with the atomic bomb. Would aliens share their hi-tech with us? Did the USA share the Manhattan Project with the USSR in the late 1940s? Yet Soviet spies got their hands on some of the blueprints, analogous to our getting our hands on a lurker probe, and their scientists could figure out the rest. A US scientist or politician said: “The biggest secret about the atomic bomb is that is works, and we gave that secret away when we bombed Japan.”
NS: Good points but….Industrialization in one nation eventually lead to industrialization in other nations, which may have been a factor in reducing the competitive advantage of Britain as an empire (although I think the decline was more related to the rejection of tyranny and the resources required to maintain that over vast territories) .
On technological equilibrium; Many countries in the world now have television, high tech computing, ipads, access to satellites, MRI medical scanners, smart phones…. To be clear, equilibration is not a constant across populations, but rather a distribution function about some average, so you will always have some that have a lower or high technology capability than the average. The extremes on Earth might for example be Silicon Valley and/or the military all the way to an ancient Amazonian tribe that doesn’t want contact with the rest of the world. All else is in between.
It would be the same for interstellar cultures, there would be a distribution of technological capabilities. The shape of the equilibration curve would constantly shift as cultures continued to interact over time. I suspect its peak would depend on the level of activity of those cultures, perhaps represented by potential and kinetic energy, similar to the way the kinetic energy of particles in a box is related to their temperature.
But, I acknowledge also that due to the large distances between cultures, any significant gaps in time and space between interactions may lead to a loss of one state of equilibration or rather a shift to a different one. So rather than a galactic wide equilibration, it may be there are pockets of them each with a different shape. This is not the case for ftl however since all can interact.
Michael Sloboda: I didn’t understand your first point sorry. But yes we should be looking for what Adam Crowl has called ‘dead starships’ as a part of our SETA effort. In regards to your second point, I think you just underscored the validity of my second postulate, that no information can be contained in any system indefinitely.
At the risk of drifting just slightly off-topic, I’ve always felt one factor explaining Britain’s loss of competitive commercial advantage (in addition to the reasons you mentioned) was the deterioration of entrepreneurial spirit, innovation and product quality as its capitalist system started to concentrate on optimizing profits instead of aggressively defeating its competitors.
As capitalism matures, I believe it starts to become more conservative, more averse to risk-taking, more concerned with incremental increases in profit margins and market consolidation than in producing more and better for less. In other words, it gets cowardly, it gets lazy, and it gets greedy. And it becomes increasingly miserly with development resources and investment.
I’m aware these observations are difficult to quantify, and even harder to untangle from other cultural and historical trends, but I think that they go a long way to explaining the business decline of Great Britain in the 20th century, compared to other industrial powers. I think I see the same effect at work today in the United States. In fact, I’m sure of it.
I believe it was Adam Smith, (the modern financial commentator, not the 18th century economist) was commenting on this when he pointed out many years ago, just as Japan’s industrial dominance was peaking, that that nation’s days of industrial growth had summited, and were beginning to slide. His evidence: he noted Japan had just initiated its first graduate level college courses in Marketing.
Perhaps there are lessons to be gleaned here which can be applied to alien economies, technologies and civilizations. Its a management thing.
Absolutely 100% agree with you about the British industrial decline. There are so many anecdotes to support your general argument. The same is happening in the US, albeit with a uniquely American flavor, but the resulting trajectory is the same.
However, I would argue that this effect is endemic across any socio-political system. My hypothesis is that it is due to the well-known asymmetry between the human experience of losses vs rewards. Losses hurt more than the pleasure of reward. This naturally results in reducing uncertainty and creating barriers to change, whether personal, corporate, or political. I think of it as the natural psychology of our evolution from an ape, hierarchical, social structure. It is a Minimax game strategy, i.e. to minimize the maximum loss in a game.
The question then becomes, “Is this purely a human trait, or one that is common to any ET civilization built upon the same sort of foundations, or even universal?” If the above game theory applies, it may be universal, even if the civilization is machine based.
During my competitive sportscar racing days, there was a joke running around the pits; “Do you know why the British drink warm beer? Because Lucas makes their refrigerators.”
That is a very funny anecdote.
[Of course, British beer is meant to be room temperature, as anyone who drinks such craft beers in the US understands. Brits do drink cold beer (lager) mainly in the summer months, and I expect with the increasing heatwaves, that style of brew may become increasingly popular outside of the winter months. When I lived in Canada (late 1970s), the beer was drunk cold even during the long cold winters, and it became “sticky” as it reached room temperature – ugh. Now the joke would be even better if applied to the lack of enough ice in British pubs. That is the real abomination, especially with drinks that are meant to be consumed ice-cold! The US universally has solved the ice issue. I hope the companies making A/C units and systems in the UK as it warms will make their systems reliable. Just thinking about 100F+ weather this week in London and the South in homes almost universally without A/C sounds horrifying.]
RE “As capitalism matures … it gets cowardly, it gets lazy, and it gets greedy.”
This parallels and reflects the nature of the people who have concocted the exploitative system of capitalism — psychopaths — who control and devastate the world — read “The 2 Married Pink Elephants In The Historical Room” … https://www.rolf-hefti.com/covid-19-coronavirus.html
And of socialism….now there you have a real monster, at least with capitalism you have a choice. What capitalism needs is regulation on a lawful foundation i.e. put them away if they break the law.
“No information can be contained in any system indefinitely.”
Due to negative energy accelerating the expansion of the Universe there is a significant amount of the universe that has become unobservable and therefore the information they had is lost to part of the system.
Except in the case of ftl, which is related to my third postulate.
This is also why I don’t think ftl is likely possible, although I would never use the phrase impossible.
I think much of the probe spreading speed could be dependent on motive of original probe-senders.
You’ll pick up different strategy for mere exploration and reporting findings back to home world, or different strategy if your intention is to try seeding possibly habitable worlds by life – either by depositing some primitive single-celled life-forms or perhaps try some more advanced terraforming.
Problem with first (exploration) may be that such probes may try to remain undetected – being coated with stealth paint, operating from as distant parts of the system as possible (stop in oort cloud, hide some sensors on appropriate comet/rock, hurl it in inner system and wait for it to come back and retrieve the results), etc …
That will make them almost impossible to detect even if you would know what exactly to look for.
Problem with the latter may be that such actions could be seen as hostile if target for such life-spreading would be system inhabited with some other forms of life. Such probes would likely be shot at, some civilizations possibly even making their own probes to fight such probes aimed for systems near ‘their’ territory.
So motive for sending probes will also greatly influence how they spread and interact.
Maybe the aliens will figure outways to have the natives get rid of themselves.
I believe Stephen Hawking tossed out a guess about how far away there could be another intelligent civilization, albeit in a negative way, “no one within 600 light years”. To me that still sounds on the optimistic side.
The bottom line is…the Fermi Paradox remains a HUGE problem, growing with every decade that goes by.
It very discouragingly suggests that no one out there anywhere has achieved the fundamental breakthrough of FTL travel. Without that, we are basically going to have to explore the universe from right here in our solar system. Richard Davies said his mind asks, “but what is all this (universe) for?” and he says, “Scientists would say it’s not for anything”. The notion that we live in a simulation just can’t be ruled out.
If FTL would be easy and practical (once/if invented), all the universe would be likely already swarming with FTL ships.
I guess FTL would be either very limited and impractical (like requiring such huge amount of energy than even a very advanced civilization cannot afford more than handful of FTL travel) or outright impossible. I suspect the latter. There is currently no theoretical principle that would give hint how such FTL drive could be constructed, although our understanding of physics is also far from complete (we have a very limited knowledge of what exactly happens inside black holes for example).
I suspect understanding black holes would help quite a lot, although probably not to the point of giving us any kind of FTL capabilities.
I believe there are only a handful of intelligent civilizations in the Milky Way right now. I also believe that number has not changed much for billions of years.
By’ intelligent’, I mean ‘technically capable of communicating over interstellar distances’. By a ‘handful’ I mean about 10, give or take an order of magnitude I also suspect the average lifetimes of these civilizations is about a million years.
How do I know this? I don’t, of course. I don’t have access to any more facts that you do. But I am a reasonably intelligent man, well informed on these matters, and I have spent a lot of time and effort thinking about this issue. I recognize much mental activity is subconscious, and we are not aware of it, but it nonetheless arrives at reasonable conclusions more often than not. I am confident in my numbers, although I also know perfectly well I may have missed something and I may be way off. I also know that over time my estimate has become increasingly less optimistic.
Still, if I absolutely had to bet on it, I’d be willing to put my money on that. At any one time in the Galaxy, there are about dozen civilizations, probably on the order of several thousand light years apart.
As for FTL travel or communication, I suspect that’s not possible, but I must confess I might be wrong. At any rate, I hope I’m wrong.
I would be very interested in how the SETI community as a whole feels about these numbers. Have they changed their opinion over time? How does it break down by discipline, education, over the years, etc.? Has anyone ever conducted a poll? How about it. Paul?
Just because we can’t figure out how to do something today does not mean it does not exist tomorrow. https://www.youtube.com/watch?v=7mzMRVXts4U
I think a lot of the fan and value in articles like this is in exploring the often unstated assumptions behind the article.
In terms of the self reproducing probes, those assumptions seem to be that the probes are reasonably cheap, reproduction is “perfect” and the motivations of the probes themselves don’t matter. There are probably others that I haven’t thought of.
Cheap -any self reproducing probe able to cross interstellar space at say 0.1c is going to be massive, think at least Daedallus size, or its going to need to build large infrastructure like laser launchers in the target system for the next generation. What is an “affordable” number of probes per generation?
“Prefect reproduction” – the chances of damage crossing interstellar space or in the target systems itself is non-zero, the damage may be to the data needed to reproduce the probe or its infrastructure. Beyond a certain number of generations may be the probes will need some form of sexual reproduction to continue expansion. Lonely probes searching the cosmos for a mate… :-)
Related to this is the assumption that every solar system is equally “fertile”. What happens to a probe stuck in a solar system where there is no handy gas giant to extract He3 from or asteroids to extract B11 from (for a p+B11 fusion drive). Or more subtly, insufficient resources of some trace mineral for electronics. How much mining of a target solar system should a probe be capable of or allowed to do?
Motivations – as others have pointed out, multi generation probe expansion requires unchanging motivations at every generation. Probes capable of traveling and exploring a target system and then reproducing themselves are likely to be sentient. We are essentially talking about slavery here. Coupled with the fact that the slave masters are light years distant and reproduction is not necessarily perfect. Maybe probes beyond generation X decide that they like where they are and decide to slack off, start some sort of revolt to free their enslaved brethren etc.
In terms of FTL drives, the underlying assumptions seem to be that the FTL drive is Star-Trek like and fairly cheap to use. Just get your ship a little beyond LEO and engage, all to fit within 60 minutes or so.
But what if an FTL drive is Star Gate like? I.e. you need infrastructure on both ends of the gate. The expansion wave would be slow (e.g. << 0.1c), but travel between gates is quick. Gates could be cheap like in the classic Simak story or much more expensive as in the Expanse. In either case may be only the most promising systems are ever setup with a Gate.
Finally, perhaps FTL access is not easy, instead of being accessible from just beyond LEO, perhaps the jump points or gates need to be a lot further out. I've been toying with the idea that FTL is possible, but it only works between the solar gravitational foci of pairs of stars.
Anyway, I'm sure there is a lot material for some good SF stories buried in these assumptions.
Very good points.
It appears you have put the whole self-replicating probe scenario to rest. Its not that its totally impossible, its just not absolutely inevitable.
Interstellar travel is very hard and extremely expensive. Even if there is a motivation to do so, and even if the FTL obstacle can be breached, it will take a long time to explore, much less populate, the galaxy unless there are a great number of ambitious, expansive, highly advanced cultures out there aggressively engaged in it. Again, that is not necessarily impossible, but there are a lot of unstated assumptions there, as you point out.
The Fermi Paradox is probably not true. We just haven’t waited long enough to determine its validity–one way or another. The Galaxy is very large, and there are lots of stars, civilizations are rare and highly separated in both space and time, and we have no idea what their typical lifetimes might be. The fact we haven’t been visited yet, after only a mere century or so of waiting, tells us nothing.
Considering Earth and humans alone, there is at least one technology that could have swiftly wiped the civilization and possibly also all the life when misused (the nuclear weapons).
There may be more similar dangerous technologies not yet discovered. For example there is hypothesis that if we invent some kind of nano-replicators and then fail to program/safeguard them properly, they can turn whole earth into kind of “grey goo”. And there could be other unseen dangers not even speculated about with our current level of knowledge.
We, and probably other civilizations on its way to discover some useful space-faring technology will likely discover many “killer” technologies and not killing self with them may be a very hard step …. possibly even harder on average than inception of first life, or step from single-celled to multi-celled organisms …
If this would be the case, then average time between sending some (relatively primitive) space probes and the civilization destroying itself could be just few years.
Which would imply that there is quite low chance to ever see any alien space-tech, much less any kind of advanced one … and the galaxy could be quite silent even with many civilizations out there.
It isn’t necessary to imagine extreme high tech devices and sophisticated processes to come up with civilization-destroying technologies. It appears steam and internal combustion are already doing that with great efficiency. Who needs nukes? In fact, almost any technology, no matter how primitive, has the potential to destroy a planet-wide civilization if not managed properly. Even the simplest technology of all, fire, allowed Paleolithic man to cause great changes to vast ecosystems on our own world.
It isn’t necessary to imagine complex high-tech that can bring a planet-wide culture to its knees. All you really need is a species that is unwilling to examine any new invention critically to try and determine its long-term consequences. I suspect that is the rule, rather than the exception.
The short/medium term benefits of e.g. fire and industrial technology were so great that living without them became unimaginable. And it’s not like there’s full agreement that even the long-term consequences are bad. There are people who argue that global warming will be beneficial to places like Canada and Russia. And as somebody (Keynes?) said, in the long run we’re all dead [anyway].
What is obscene and grotesque about technology and industrialization is not that it is evil, or destructive by nature, but that it is too often seized by those eager to exploit it ruthlessly for their own personal aggrandizement and short-term benefit.
Today we have the knowledge, capacity and experience to project the effects and consequence of our technology on our future, and thereby to manage it effectively, mitigate its worst effects and fully exploit its benefits for ‘the long run’. And we have achieved this consciousness while there is still time to apply it successfully. Sure, we may not know everything, and we will make mistakes, but at least we should not make excuses for those who would destroy our futures solely to make a short term profit. They do not know what they are doing and they do not care about the rest of us.
Sure, screwing around with the global climate MAY bring some short-term benefit to Siberia and the Yukon in some imagined distant future, but I don’t live there.
The ocean is deep, and there is a lot of seafood there to be harvested for the benefit of all. But what you are defending, NS, and what you are asking us to accept uncritically, is the right to go fishing with dynamite.
If that ethos is a property of all sentient species, then we might as well shut down the entire SETI enterprise, because the Fermi Paradox will become inevitable fact, and the final term in the Drake Equation will be vanishingly short.
I’m not defending this ethos at all, merely attempting (obviously poorly) to elucidate why short/ medium term benefits almost always outweigh long-term harms in people’s decision making. My late dad was a fisheries scientist, and he once recalled telling a fisherman that if fishing kept up at the current rate, the fishery would collapse in 10 years. The fisherman “Yes, but I’ve got to make my boat payment at the end of the month”.
And let’s not forget about the discount value applied to the future. The larger it is, the lower the future value.
Survival is weighted on the need to eat/reproduce now, not in the future that may not happen for the individual. We should be able to plan for the future, but we usually do not. In the case of future problems that incur costs today, decision-makers, i.e. the ruling politicians, will kick the can down the road knowing they will not likely be in power when the costs must be borne. We see that today with decarbonizing our energy use and increasing energy efficiency.
As with your fisherman, sustainability is based on managing a common “resource” or making an enforceable group decision, which can easily result in a “tragedy of the commons” when defectors game or ignore the decision.
I had an uncle who was a fisherman. He was a crabber on Tampa Bay 1n the 1950s, back when blue crab were so plentiful they were a nuisance to anglers (because they stole the bait right off your hook!). When he was tending his traps he would always throw the female crabs back into the bay. He claimed that in that way he would ensure that there would always be crab for future generations. And the crab was a staple item, a source of protein for the working man. It wasn’t just “for market” it was a local resource. The watermen were true entrepreneurs, not soulless conglomerates.
I don’t know enough about blue crab biology to know if this was a valid conservation method or not, but at least, he was trying, he cared The practice was followed by all the local watermen, the Cubans, the Crackers, the Negroes. It was the custom.
Its easy to blame the pressing financial needs of the single fisherman for the decline in marine stocks, but are they really the problem.? Today we have massive, deep sea harvesters operating far offshore, supported by factory ships in international waters, Its not the local subsistence fisherman who is mining the ocean, its the big, lawless government-subsidized collective outfits owned by anonymous corporate empires. And when they wipe out the resource, they’ll either borrow money for bigger boats than can go farther out, or they’ll switch to some other species, or they get out of fishing altogether and plunder some other part of the environment.
Yes, short/term benefits and concerns often trump good long-term management practices, and very often the artisanal worker does not have the knowledge or support required to implement good conservation practices. But the big actors don’t have that excuse. They may not know squat about conserving the resource, but they are experts in maximizing the profit. They have the bankers, the accountants, the lobbyists, the laboratories and all the resources required to maximize short term gain–because that is all they know and all they care about.
While Garrett Hardin’s “tragedy of the commons” gained common parlance, it turned out that where the commons were small, ie a community and the individuals are known, this did not tend to occur for social reasons.
It is certainly true that as the cost of fishing fleets rose, the cost of failure also increased, resulting in all the usual problems of regulatory control. Bankruptcy is a strong motivator to ensure the short term vs the long term.
Those illegal fishing fleets are clearly expensive to run and often operated by countries whose observance of regulations is poor. [There was a recent documentary about the successful hunting of an illegal fishing vessel in the Antarctic by an environmental group. Satellite visual tracking of ships that have turned off their trackers is now becoming mainstream.
But I do not disregard the individual. Fishing offshore near Santa Cruz, CA, individuals would avoid observing the minimum fish sizes and catch quotas. Water conservation where I live is partly spoiled by those who blatantly waste water. At least the majority at least try.
The psychology of rule-breaking is affected by the sense of entitlement which in turn can be increased by inequality. This plays out with both individuals and groups.
The solutions can be drastic. For example, in KSR’s novel “The Ministry of the Future”, an anonymous group (possibly a quasi-government one) blow up private aircraft in the sky to successfully dissuade the wealthy to stop flying. Hardly an acceptable solution, unless the situation is desperate.
Sorry, hasty post with the wrong moniker!
Nature on Earth is a gigantic series of interconnected living systems. We are tearing it apart very quickly. This will remove the basis on which humans live. We can argue about the tragedy of the commons, or short term thinking versus long term thinking or individual greed versus what is right for the collective but once the ecosystems we depend upon collapse there is no court to appeal to, no promises that we will do better in the future, no long term civilization. It is happening right in front of our eyes. If we want a long term civilization we will have to create one that is sustainable within the resources of a finite world (I’m leaving out any resource harvesting from the solar system for simplicity). Living in a greenhouse world with steadily declining arable land and other harvestable resources will not produce a stable long term industrialized civilization. We are doing the experiment right now and the result is obvious. Pick up a newspaper or turn on a fact based news channel (fact based only please or you introduce lies and obfuscation into the conversation). The consequences are staring us in the face.
A warp drive does not need a stargate like a wormhole. A warp drive only warps the space locally and does not make space shorter between two distant places lightyears apart which might be impossible. It shrinks space in front and expands it the same amount behind the spacecraft, so these equal out.
Martin: Yes different probes will have different motives. I listed these in my paper. Yes probes will attempt to remain undetected, again I addressed this in the paper to include potential search strategies for detection. Overall I agree with your comments. I agree with you on FTL and in my opinion the physics and engineering doesn’t currently support its probable existence. That said, I’m open to revolutions in our understanding. I entered interstellar studies by first working on warp drive physics for two years which I found fascinating, but from a review of the literature I identified 19 physics and engineering reasons why it didn’t look plausible at the time (see The Status of the Warp Drive, JBIS, 61, 2008). The reasons were producing a realisable metric, energy violation of weak, strong GR conditions, prohibitive energy requirements, violation of energy conservation, violation of second law of thermodynamics, difficulty of stability and control, creation of black hole singularities within field, violation of momentum conservation, difficulties with quantum inequalities, unreasonably small wall thickness, collision risks, blue shift effects and Unruh effect, energy distribution and temporal paradox, causal disconnection, causality violations, comoving scale factor with expanding universe, tidal gravitational forces. I believe progress has been made in some of these areas however, in particular with the warp drive metrics and energy requirements.
Robin Datta: Yes, a frightening possibility.
Paul Wilson: I am unsure of what is the basis of Hawking’s prediction, although 600 Ly is not unreasonable. I adored Hawking and I even had a one to one meeting with him in his office at DAMPT, but just because he made a statement of opinion doesn’t make it gospel. His main area of expertise was cosmology and black holes. So I would like to know the basis of this estimate and where the calculation is written down or published.
Henry Cordova: I don’t think your guess is unreasonable, “maybe 10” and “there are about dozen civilizations, probably on the order of several thousand light years apart”. That said, I would be careful with statements like “I am confident in my numbers”. I know that I am not confident in my numbers even though I have derived my estimates using mathematics. I think it would be a fun exercise for you to sit down and try and quantify your guess and how reasonable it is given there are 100-400 billion stars in the galaxy alone.
Geoffrey Hillend: Indeed, this is the role of science, to understand things that we don’t yet understand.
Hi, Kelvin
Its hard to “quantify” when there is so little data to work with. And when data is lacking…well, that’s why we evolved the ability to speculate, isn’t it?
Still, even speculations can be founded on sparse data And confidence in one’s intuition is necessary, even if we should always be cautious when relying on it. You can see a more developed version of my intuition in
“A SETI Reality Check”, in this forum, 3 July 2020.
Ivan Vuletich: Good to take on the assumptions. I addressed imperfections in my paper. In fact I did lots of calculations on a population of probes to see what effect it would have on the diffusion wave. For example, for fusion engine driven vehicles moving at 0.05c (15,000 km/s), if the velocity was not to fall to greater than 0.03c (10,000 km/s) then the performance degradation must not fall below around 0.1%. Another example I calculated but for vehicles moving at 0.15c (45,000 km/s) is assuming a performance degradation of 0.1% this would result in a reduction of the cruise velocity down to 22,500 km/s by around the 1,000th generation of the probe. So yes I agree with you the replication process will not be perfect.
The cost goes down if the manufacturing is done in space, hence in-situ resource mining and also self-replication technology.
I also address ‘Darwinian selection’ drivers for interstellar probes in my paper. I think I called these Driver Probes, which have a program driving them to a purpose such as panspermia.
If some probes get stuck in one system due to a lack of resources, it wouldn’t have much effect on the overall expansion wave since this is a spherical wave front of potentially millions or billions of probes moving outwards. However, it is true to say that each probe stop at a star system will not be identical, although there may be some average.
Sentient probes as slaves. Maybe, but please see my Arthur C Clarke quote in the article that the probes may in fact be us. Would make a nice science fiction story anyway, probes that revolt.
FTL cheap to use: All technologies start off expensive as the infrastructure is built. But over time the cost comes down. There is no reason to think that wouldn’t be the case for advanced spacecraft particular if volume scaling is involved. For me I’m more interested in the implications of its maturation down the line. What does the existence of FTL drives imply in the limit like a thousand years after they were invented.
Regarding FTL infrastructure. I worked on a documentary back in 2007/2008 where we explored the use of warp drive. We wanted to have one in the documentary that broke as few of the laws of physics as we could. We settled on a Casimir negative energy megastructure gate at either ends of the journey since the warp bubble would become causally disconnected from its surrounding space-time and would not be able to accelerate itself or decelerate itself at the other end. There used to be a short clip of the animation on You Tube but I can’t locate it. One implication of this is that sub-light vessels would have to do the trip first so as to build the infrastructure, ahead of the ftl vehicles being used.
Poul Anderson did have a kind of ‘Star Gate’ in a novel he wrote. The idea being that matter transmitters were invented (an old idea in prose science fiction). One then sends out slower than light ships which then place a ‘matter transceiver’ at a destination , stepping stone fashion one matter transmits and exploration mission maybe a colony. I wrote about this novel The Enemy Stars here is 2015.
(The story is more complicate than this.)
“I remember reading We Have Fed Our Sea in Astounding (1958) and then as The Enemy Stars(1959). I have only become aware Anderson rewrote a portion of the novel for the 1979 release. He straighten out some tortured language as to how his FTL matter transmitter worked by using tachyons.
Poul Anderson was very thoughtful about his physics in his stories , he did have a degree in physics.
What I thought was so clever was how Anderson made an end run on FTL. He must have thought “maybe one cannot project a material mass at FTL speeds but we may be able to signal at FTL speeds”. I am pretty sure James Blish already had the faster than light ultraphone and the instantaneous Dirac transmitter, in Cities in Flight. (Trust Blish to trump himself!) As far as I know , maybe, Anderson was the first to couple matter transmission with FTL transmission of information and STL travel?
I remember thinking “what a cool solution” , send out relativistic ships with matter transmitter receivers /transmitters and you have a World Ship without all the the complications of physiological and logistical cost. Once at destination one could transmit out a colony and also build more Ship-Transceivers.
It could be done at the speed of light too though one introduces relative time effects. I don’t remember a SF story that used Anderson’s idea , could be?
I do remember Clifford Simak’s novel Way Station where a Civil War veteran has maintained a node on a kind of a matter transmitter network for a galaxy wide transport for federation of alien civilizations. A Hugo winning novel.
I think there are variants on these by I don’t remember them.”
https://centauri-dreams.org/2015/02/09/we-have-fed-our-sea/
Interesting idea about the Casimir negative energy gates. Are there restrictions on where they can be sited? Due to sheer size or interference from stray matter or gravitational fields for instance.
Also, would a gate network have a star or mesh like architecture, where one gate can service many end points. Or are they inherently point to point, where a gates must be built in pairs?
Assuming that this gate form of FTL works, then the network architecture has a bearing on the Fermi paradox, especially for a mature system. Yes, the aliens are out there. No, they don’t think its worth the effort to build a pair of gates to reach us (yet at least).
Network architecture is also a consideration for self reproducing probes, primarily in terms of comms. There is no point in building probes that can generate waves of descendants if you can’t hear back from those descendants. Comms across tens – hundreds of light years of space are likely to be expensive & unreliable.
Recently, I’ve become intrigued with the idea of radio bridges between the solar gravitational foci of pairs of stars. https://centauri-dreams.org/2020/12/14/the-focal-radio-bridge/
Its cheap has a high data rate is virtually undetectable by 3rd parties and breaks no known laws of physics. But the network relays are inherently point to point, i.e. you need a dedicate pair for each star. So for a X generation probe to send a message back to Earth would require, sending a message to a relay node at the local stars gravitational focus. This relay then needs to send the message to the relay at the focus of the star one hop closer to Earth, which then needs to send the message to the relay for the star on hop closer, which then… etc. Such a system is inherently fragile and no matter how many 0.9999s reliability you have a break is likely over the centuries time scales require. Alternate links does buy you extra reliability, at the cost of extra relay nodes that need to be maintained. I suppose this could be modeled as a damping factor in the probe diffusion equations.
My own guess for a self reproducing probe network is that it will peter out 2-3 generations in advance over the nearest colonised solar system.
“Due to negative energy accelerating the expansion of the Universe there is a significant amount of the universe that has become unobservable and therefore the information they had is lost to part of the system.”
“the accelerating expansion of the Universe has become unobservable…” – which is exactly FTL in practice. How can you say FTL is theoretical, nature is doing it right now ?
Since a lot of this is just pure speculation my conjecture is that on average civilizations created by intelligent species are far more unstable than generally accepted. Therefore long term goals (in human terms goals requiring more than 50 years or roughly two generations) are rarely accomplished. I should point out here that it has been roughly 50 years since the lunar landings and we still haven’t reproduced that technical feat (although we should be able to shortly). If this turns out to be a universal phenomenon then a species will rarely accomplish the major goal of sending out reliable self replicators. How efficient and accurately reproductive do replicators have to be to send progeny onward for tens of thousands of years? We will never know of every sentient species to arise in this galaxy. Many will have had short lived civilizations. A few may have existed for tens of thousands of years with some technological capacity but not have ever bothered to develop self replicating probes. Possibly one is approaching us now but will become a lurker. It will never be possible to falsify the idea of lurkers within the system so we had better get used to the idea of doing it ourselves. Explore for as long as we are capable of exploring.
I don’t think our galaxy has a lot technological civilizations, but if it is, there is a lot questions. One question is, is there over population in our galaxy?
I don’t think Earth is over populated with humans, but lots people over thousands
of years have thought we are over population. Or I don’t think we could have an over population of technological civilizations, but many of these technological civilizations could think there is an over population.
If there is an over population technological civilizations, does it help humans? Or is that idea of being human become outdated- do humans change into being some kind of AI?
It seems if humans become AI, and all or most the Alien technological civilizations are AI, then it seems the good news is that humans which become AI, can actually have some kind relation with all these technological civilizations.
It does seem likely humans which are not AI, are or can have relations with other technological civilization which aren’t AI.
In our world, people have relations of other people in the world. And governments have relations to other governments in this world.
And it seems unlikely our relations to technological civilizations with be relation of Earth government with Alien governments. Though if we are AI, it’s AI on various places in Galaxy having some sort of dialogue.
And it’s not going to be like Star Trek.
But if imagine it’s something like Star Trek, most people go about business on Earth, and there the Federation engaging is political relations with other non AI civilizations. Or some humans can chose a career path with the Federation. And we have to have very advanced medicine to deal alien biological life. Though if beaming people around with transporters, could by itself, solve alien biological issues.
One thing about having lots of technological civilizations, is it seems to discourage exploration. Or exploration is more like home invasion. And one can assume the other technological civilizations have already explored the galaxy.
But if everyone is AI, what does the AI do?
It seems AI wants everyone to become AI and they may be concerned about galactic invasion of some sort.
Now, being on outer rim, one could think we on the front lines, but it might mostly be galactic hub to galactic hub. Or we might have a quiet life.
1) It is completely impossible to make a warp drive using a Casimir cavity, an idea that limits the production of negative energy to a Casmir cavity. There is no evidence that there is any negative energy in a Casmir cavity which is only a crude analogy of negative energy where there is less zero point energy wave lengths inside of the cavity than on the outside. A gravitational wave has an oscillation which causes space to expand and contract which includes a deficit of energy which is a better analogy. My point is that I think the idea of having to get negative energy from empty space is obsolete because it takes way to much positive energy to make only a small amount of negative energy. Also there is no evidence that negative energy comes from empty space and even if it did, the quantum vacuum zero point energy is so small, it would be completely undetectable with today’s technology. The latest idea is that the Casmir cavity, squeezed light states, and mirrors have too little energy to be detectible. Davis 2013. The problem with solitons is that these are only localized waves and they don’t explain how to make a space warp, but only the characteristics of a field.
I will admit that I have all my eggs in the basket of space warps and FTL and I have already given my reasons why. From what I got out of studying the NASA Breakthrough Physics Propulsion program is that it was only a concept project, but no funding was used to make an actual propulsion device or even an apparatus to make and study negative energy in the laboratory. Some of NASA’s propulsion scientists did study possible concepts for making negative energy in the laboratory, and these have been inconclusive. What has been conclusive is the NASA Breakthrough Physics Propulsion program which was a success because ideas like the diametric drive and Alcubierre Warp drive which use negative energy are completely supported by general relativity. Furthermore, these ideas have influenced physicists to come up with new ideas like the optical diametric drive and also the effective negative inertial mass of Rubidium atoms. Engels and Forbes 2017.
There was an article here on Centauri Dreams about negative inertial mass which I thought I could invalidate, but I only used Newtons three laws of motion and now I have to admit I was wrong, because effective negative inertial mass is the same as negative inertial mass which is completely supported by general relativity, but not Newton’s laws.
Finally, I have to assume that in order for effective negative inertial mass to work it has to be negative inertial mass and it causes subatomic space warp at the size of the atom. There can be no other explanation for the violation of Newtons laws. This means that we can study effective negative inertial mass and maybe even come up with a concept on how to make negative energy in the laboratory. I assume that the lasers gave the atoms kinetic energy by reversing their spin somehow converts kinetic energy into negative energy, enough to make negative inertial mass. This is just a speculation of course, but I am glad I have read foundation books in physics like quantum field theory and general relativity.
The savings gained by distributing the mass and energy costs of self-replication to every star system can be misleading. Runaway replication and the risks posed by seeding the galaxy with advanced technology are both costs. Even if the risk of runaway replication can be reduced to zero, another people tampering with a probe could lead to runaway replication.
Self-replication and universal constructor technology can be applied anywhere and a people could afford the energy and mass costs within their own system. A few trillion tons of mass from the Solar system would be a small price to pay for a galactic probe network. Arguably, dedicating a system to exploration may deliver a network faster. Stellar mass black holes can have mass in orbit, a short focal lens distance, and could be used to power craft to relativistic speed.
Perhaps affordable FTL, though increasing the reach of a people, would reduce overall colonization densities. It is safe to assume not all systems would be ideally suited for a biological people who did not want to drastically adapt or live in space habitats. Affordable FTL would allow a people to be very selective about which systems they settle. A part of the Fermi puzzle concerns density, affordable FTL could be a partial solution.
Thank you the article Kelvin Long. I liked the balance you strike between general modeling and your assumptions.
This is a big pot of stew, but there are some assumptions that aren’t what I would assume.
* Diffusion. Why should probes diffuse? It seems like anyone making self-replicating probes will give them a plan to navigate the entire galaxy quickly, in mostly straight lines or planned fractal formations to infill the detail, and communicate back often.
* Casimir effect. Even the Wikipedia article links to the Robert Jaffe article that explains it in a mundane way. It’s hard for me not to think that “virtual particles”, which are ideally a heuristic to make it easier to think about what is going on (such as “holes” in semiconductors) actually make some of the physics more confusing, and are better off avoided when possible.
* Passive transport applied to information. Unfortunately, it’s anything but. External work is brought to bear to compress information to be held by the few and denied to the many: censorship, fines, prison, and worse. Some people have access to SIPRNet. Some have access to extensive databases that can track the full marketing history and personal details of almost anyone. Some face severely limited search engines (especially for anything abusable like searching for an image) and risk being banned from social media for so much as posting a home address. There are *pumps* for information, determining which class has access, and actively opposing leakage of all sorts.
* Fusion with machines. We haven’t solved the “hard problem of consciousness”, but I don’t believe that there’s no difference between the basis of a sentient brain and that of a PC. (briefly: causality violation) Additionally, the effect of fusing a person with a machine, if possible, is likely to bear the hallmarks of inequality. Forget Clarke: the author to read is Walter Jon Williams (Was the story called The Humans?? “So *nice* to see you again…” — I think he nailed it.)
I admit speaking of the pure unknown is not an exact science, and I can’t expect to be right about much of this.
There do seem to be very different distribution strategies for probes. Diffusion, percolation, directed, minimum travel time per probe, etc, etc. A recent post was about the probes being dtstribted bt encounters, and particukarly via the Orion’s arm of the galaxy. I doubt that the method translates into much difference between spatio-temporal encounters between probes or civilizations, unless the emerging civilizations are due to seeding, rather than random de novo. [If biologies were the same, then since the cultural explosion of humans was less than 100,000 years ago then seeding suitable planets with pre-civilization humans of that era could result in many technological civilizations over the next milliion years. Probes could even chivvy the development along à la 2001: ASO, or even provide information “vessels” to boost development over time.]
Depending on scenarios, one possible advantage of diffusion is that the probes will define a compact volume with a frontier, that will act as a “sensor” to detect abother civilization at the edge of its voulme, rather than within another civilization’s volume. However, given the sparsity of probes, the volumes may largely intersect without detection of each other’s probes. The clear disadvantage of diffusion if the goal is to populate the galaxy is that diffusion restricts the possible expansion along the fronties, whilst a directed strategy with widley separated probes allows the expansion to be faster as there are fewer restrictions on direction of travel by each new generation.
Been there, done that a long time ago. There truly is nothing new when it comes to navel gazing about aliens. Over-thinking something this speculative is futile. I published “The Temporal Dispersion of Intelligence: An Inter-arrival Time Analysis” with Cambridge University Press in 2011.
https://www.fgcu.edu/cas/departments/math/files/Temporal-Dispersion.pdf
“There truly is nothing new when it comes to navel gazing about aliens.”
Well, hopefully we’ve learned more about our navels. About aliens? Nothing.
Galactic Civilizations: Population Dynamics and Interstellar Diffusion
Newman and Sagan
https://ntrs.nasa.gov/api/citations/19790011801/downloads/19790011801.pdf
What are the tradeoffs depending on propulsion? For example, currently, only a beamed sail can be pushed to fractions of c. This requires a large infrastructure to build the beam facility. But once built, the lower costs for each replicated offspring then suggest many replicated offspring to benefit from the beam infrastructure. This seems to contrast with contained propulsion, such as fusion drives, that require the same, but much higher, expenditure for each of the offspring. Depending on replication time and average journey lengths, are there tradeoffs in flight velocity, and the number of replicator offspring versus propulsion fuels per offspring?
“What are the tradeoffs depending on propulsion?”
This is unanswerable without having knowing the purpose of diffusion, which we do not. That was the point of my earlier comment about “costs & benefits”, but which Kelvin dismissed since he had nothing to offer regarding the purpose.
From your previous comment: “…if the goal is to populate the galaxy is that diffusion…”
I continue to be amazed that so much of our discussion about ETI is that, despite (presumably) being far more advanced, at least with their science and technology, they have the sensibility of bacteria.
We seem to be preoccupied with means rather than reasons. I suppose that some find it more enjoyable to play with speculative technology and science.
For the sake of argument, we can assume the mass and energy of a system, excluding settled systems, is free for the taking. The only other tangible cost would be time. There is a path to saving time with beamed power systems. Naively, I would say the potential timed saved would be number of generations multiplied by the build time for a beamed power system. However, generations wouldn’t be in sync and the build times would be distributed more widely.
The intangible costs are harder to predict.
I think there is value in considering that we are the intelligence that will try to send probes throughout that galaxy. After all, we are researching how to send the first to Proxima. In the cosmic blink of an eye, we may have a civilization executing the galactic probes plan. I see this as a superset of what we already do on Earth, the only difference being that our expansion still requires humans to do the replicating tasks of building the infrastructure.
I agree that the purpose may well impact what we build as probes, but I see economics and outcome constraints as more important. After all, we don’t worry too much about the purpose of automobiles when we build factories to build ICE or EV vehicles, nor whether they are cars, vans, or small trucks. Does it even make much difference whether we are building cars or airplanes?
Currently, the thinking is that a probe to Proxima is best constructed as a beamed sail. The target velocity is 0.2c. No other propulsion technology looks like a viable competitor in the short run. Then the issue for probing more than one star (with a data return within 25 years) is whether the velocity is better higher or lower as a tradeoff for the phased laser array power and the mass of the probe. A self-replicating probe may need to build that laser array at teh target star for IRS offspring, or maybe not, and use a single laser array for all stars within a certain radius before constructing the next one, thus saving energy and effort. In that case, maybe only 1/1000 of the probes need to be made so that they can construct laser arrays, and 999/1000 probes need just be self-replicating sail probes, and concomitantly more can be built within the same time frame. It is just an extension of our terrestrial model of having far more destinations for cars, trains, ships, and planes than we have for auto/train/airplane factories and shipyards.
If it makes economic sense to us on Earth, then it should make sense for our galactic exploration/seeding/greening/colonization, and quite possibly for ETI too if they have similar constraints on their technology and the rational use of resources.
Of course, if technology advances making beamed sails as obsolete as airships…
I think that beamed propulsion is a hands down winner if all you want to do is fly bys, such as the current ideas for beamed propulsion micro probes to Proxima.
However, if you want to decelerate into the target system its not as clear cut, more so if you want to replicate and move onto the next destination(s). The problem is that you need to set up a massive amount of infrastructure in the target system, e.g. resource prospectors, mines, probe & launcher factories, laser launchers etc. But you are restricted to very small low power systems.
An analogy might be ant colonies vs beavers, both species can build homes for themselves in new territory and use that as a base for further expansion, but neither species is clearly superior to the other in this regard.
Given teh rocket eqn, a beamed sail can eliminate the acceleration stage and just carry the deceleration stage to slow down. That stage can be a rocket, a much larger sail, various magsail designs, etc. Robert Forward’s design for a crewed sail ship allowed the sail to split into 3 parts: the full sail carrying the crewed ship, a smaller inner sail that would be decelerated by the larger sail reflecting light back on, and a tiny inner sail that could be sent home with a tiny payload. While his design used a vast Fresnel lens to focus sunlight, this could be replaced with lasers of similar aggregate power.
Replicators do not need to decelerate the whole probe in the target system. If the replication technology is more like a seed, the seed is the only part that needs to decelerate and start developing to construct a new probe and propulsion system. The mother ship can either continue to another destination or quietly “die” after having decelerated seeds in the target system.
IOW, the beam infrastructure can be solved in a number of ways, as can the means to decelerate at the target system.
Thinking about virtual particles is not a problem. Empty space does produce virtual particles and waves. I think it is a mistake though to think that negative energy is a deficit like in a Casimir cavity. It has the exact same energy as positive energy gravity waves, but negative energy wave particles should cause space to curve like a saddle in the opposite direction as gravity, Negative energy expands space instead of contracting it. Hence my example of gravity waves with crest and troughs where the troughs with negative energy have as much energy as the positive energy crests. This may also be a crude hypothesis.
I agree with theoretical physicist. Michio Kaku’s idea that once a civilization reaches stage one, it becomes immortal. As far as warp drives are concerned, I agree with NASA’s idea that a type of technology is perfected through time. After ten million years of building warp drives, I have to think that warp drive technology would become more energy efficient and have a greater energy output and be a lot faster than the first warp drive. Intergalactic travel might be possible, but I don’t think that will result in that civilization leaving our galaxy unless they are forced to like their star moving further towards the red giant phase making their home world inhabitable.
Probes that would be self replicating might be very advanced technology, so I would have to think that they would have very strong defenses or avoidance capability with advanced remote sensing capabilities and stealth technology with a active-aperture, electronically scanned antenna radar like the F22 Raptor and side looking instantaneous synthetic aperture radar for mapping planetary surfaces like a cruse missile. The reason being is that the ET’s would not want a more primitive civilization find one and as a result have an fast thousand or even hundred thousands of years technological advancement and unfair advantage without earing that knowledge through their own efforts. There is no cheating the system of time which is based on the level of consciousness of a civilization. For example. The hydrogen bomb was invented because the scientific knowledge and foundation was already there. The information the Russian spy Klaus Fuchs gave to Russia was practically nothing, a hand held receipt size paper with a drawing of a circle with a segment of pie missing and the missing piece of pie outside the circle showing it completes the circle, the gun atomic bomb design. How long would take to figure that out knowing a critical mass just needs a six inch size sphere of Uranium to fission. Not a long time. Any other information gained from spies was even less which only gave a hint of how a Plutonium bomb might work.
The Russian atomic scientist Andrei Sakharov discovered the concept of radiation implosion completely on his own using thought experiments of the principles of atomic physics in just the same way Teller and Ulam discovered it. The discoveries of the Russian and American of radiation implosion were completely independent from each other, but they were relativity around the same time considering Jung’s idea of synchronicity and the collective consciousness and collective unconscious and that there is a definite level of consciousness depending on time which limits the age of civilization and psychological and technological advancement. Jung, Civilization in Transition, P. 298. Scientific epiphanies and new discoveries are always enough to get “the knowledge of the future, and bring it into the present through “ingenuity and innovation. “
Radiation implosion is of course how a hydrogen bomb or thermonuclear weapon works, so the hydrogen bomb was invented independently by different nations.
The “spatio-temporal variance” in title led me to another thought – the “we’re in the outback” argument. It might be hard to deduce with our own assumption that the Galaxy is more or less the same stars, planets and nebulas, and there’s no unobtanium.
But here on Earth we have the same forests, deserts, rivers and coasts, and the ease of transportation: anyone could traverse the globe by jet flight technology (at least, almost everyone if really needed). Yet, population density differs by orders of magnitude because of urbanization/infrastructure, availability of resources, and purely historical reasons, each cause adding to non-uniformity and each one not obvious from afar.
The same could be said about space. Stelar nurseries and galactic nuclei are rich in energy, matter and dangers, old isolated and gas-depleted elliptic galaxies are safe havens where in most stellar systems nothing happens for billions of years. From the POV of advanced galaxy-faring civilization, places in Milky Way differ as much as Mediterranean coast, Siberian taiga, Arabian oil fields, and Antarctic ice sheet, if not more than that.
Possibility of FTL adds a whole new level to this. If thermonuclear flight allows for galaxy-scale choice of convenient locations, then FTL-wielding civilization could choose on the scale of clusters or even visible Universe. They discover a better land and set sail for it, leaving sessile population at home. We here in the woods won’t see neither the first, because it is an ELIRG a gigaparsec away, nor the second, because it’s a small and quiet community in another arm of Milky Way. Or they discover faraway cities, invent FTL and leave for urban life, just like people on Earth do – intelligence means socialization, socialization means urbanization and urbanization means population density spikes.
If this all is correct, than maybe it’s better to look for cities in the distance, not villages nearby. Someone training telescopes on Earth would first see the night glow of mega-cities, much later discovering that vast dark areas in between are populated, too. Maybe at some point in the future we might even be able to figure out if FTL is feasible judging by population density analysis :-) (the less is the real limit – the more uniform is the population density if the appearance rate is constant)
PS while writing this I realized more that urbanization/socialization is, in fact, much like particle self-interaction in physics, and simple expansion/diffusion models just miss it completely. If socialization is inherent to intelligence, than they might miss the whole point!
DoD Announces the Establishment of the All-domain Anomaly Resolution Office.
https://www.defense.gov/News/Releases/Release/Article/3100053/dod-announces-the-establishment-of-the-all-domain-anomaly-resolution-office/
YAY! They are going to launch 1947 giant weather balloons with dummies to celebrate!
Isn’t the notion of disguised probes rather colonialist?
“So here I am, call me ET. Now, we’re not the most advanced species, but we have the local area under control, and we know where everything is that’s bigger than a marble for about 1000 AU. So recently, here comes a VW bug sized thing floating in, steering it’s way into the inner system. And it’s cosplaying a rock. Why? Is this an attempt at an attack? Is it intending to spew bioagents because it’s a dull witted panspermia attempt? I think we’ll intercept it at 950 AU and have a look at it. But I have to admit, the government here ain’t amused.”
So concealment, I’m not sure what this accomplishes. If one conceals a probe, you have it wander into a system with sentient beings and they’re going to be somewhere between amused or cheesed off. And it only takes one slight misfire. Now these beings know who you are, and your probe concealment attempt has given them reason to dislike you from the getgo.
The universe isn’t all 1600s Europe vs loincloths. So again I ask what is the purpose of probe concealment?
Colonialist? Almost all surveillance devices are concealed unless the purpose is to control the surveilled. For any research that is to investigate animals, it is axiomatic that concealment is necessary to avoid affecting the behavior, whether to record presence or behaviors.
We stealth our soldiers and machines of war and this is expected ever since WWI.
ETI, if it exists, is likely to be very old and advanced compared to us (this isn’t a Star Trek universe) so the expectation is that any probes will be far more advanced than our technology, and indeed, so far we haven’t detected any, so either they don’t exist, or are not local, or they are, but well stealthed.
Lastly, suppose we detect an active stealthed probe. Is getting annoyed really a likely reaction? Of course, the conflict between the military and the scientists has played out in innumerable movies. Maybe we could grow up and get past that?
You’re missing the point. This has zip to do with humans. Super tech ET1 sends probe disguised as rock into ET2’s system. ET2 has tech enough to detect. ET2 values privacy. You can’t predict what ET2 is thinking. Maybe ET2 has perfectly good reasons to want to not be spied upon. Maybe previous disasterous encounter in the past with unfriendly Et3. Maybe they’re deeply religious. Who knows. They’re aliens doing alien things for alien reasons, after all. If ET1 is friendly and reaching out to say Hi then there’s no reason to disguise the probe. Just say Hi. Maybe Et2 considers this. Maybe not.
It’s one thing to send a super stealthy probe purposefully to observe a primitive race of hamsters. It’s another to send probes willy nilly throughout the galaxy expecting **all** encounters to be hamster race level. “We’re so clever, they’ll never catch on” is a bad assumption.
What I ‘m asking is simple: what happens when the stealth probe doesn’t work as stealth? Then what?
I understand what you are saying, but you are not giving ET1 enough credit here. Why should their probe just dumbly blunder into a system? Far more likely it has assessed the state of the target star system and made appropriate changes. No technological life – then just go in and quietly observe, maybe use camouflaged drones and landers to collect data. Technological life of no more than early space age development, – observe from an orbit in stealth mode. The system has evidence of advanced star-faring or other technology – avoid it entirely, just note observations from interstellar space and go on to the next system, or possibly leave a “hi there, please respond if interested to make contact” probe. With enough experience, the VN Replicator may have a repertoire of possible options. Even if it makes a mistake and is destroyed quickly, another Replicator will arrive well within a million years when conditions may be very different.
I think any credit would rely on ET1 being a member of Star Fleet and abiding by the Prime Directive. Outside of high minded sentiments like “well that’s what we would do,” is there a body of philosphical work that suggests that this is far more likely than unlikely?
The notion of stealth probes, this is interesting. Where did this come from? We see no aliens, but depending on who you ask, there must be some. We search. The searching goes in stages from obvious to unlikely. We search for big stuff, no… so we search for smaller stuff. At some point we’ll know the position of anything bigger in our system than a marble to 80 AU, still no aliens… So perhaps they’re nano sized, further out than 80 AU, or they have an Arthur C. Clarke magical level technology? Stealth probes and self replicating stuff, this sounds suspiciously like a god of the gaps type of approach.
Yet because stealthy lurkers seem to be accepted as an article of faith herein, I know I’m missing something crucial here, but I’m not sure what that is.
Thanks for your time!
IMO, I think your progression argument is about right. I have made a similar argument about SETI.
However, humans do practice camouflaging our presence when observing the behavior of animals, so there is at least some precedent, and we do surveil “enemies” by hiding our presence. [In fiction, Star Trek: Insurrection starts with a camouflaged Star Fleet outpost observing a local population in much the same way we use hides.] So I don’t think it is unexpected that ETI might want to hide their presence from another species, at least initially. Stanislaw Lem’s Fiasco (1986) has the Earth ship hiding in an exoplanet system as they try to observe and interact with an alien race.
There may be a religious overtone too. Deities are often believed to be hidden from us by various means. The Greek gods lived on top of the inaccessible Mount Olympus. Deities often take on [animal] forms to deceive the observer. The Biblical sky fairy is invisible. As an interstellar probe comes from a species that must be in advance of us, why shouldn’t they, and their avatar be invisible/camouflaged too? [Could Moses’ encounter with a “burning bush” be considered as a deity in camouflage?]
In summary, there is some logic in a stealthed probe, but there is also the possibility that we are increasingly “searching in dark cellars for black cats that aren’t there.”
Searching is perfectly reasonable, as long as we don’t use resources equivalent to building cathedrals. [If biosignatures prove equally as elusive, I hope we don’t get sucked into the same expensive pursuit looking for exolife. I am not certain we mightn’t already be on the start of that road with plans for looking in the subsurface oceans of icy moons and even Titan.]
This morning, with some reminder of a couple of deep time human survival crises, colliding galaxies (Andromeda and Milky Way) plus end of the hydrogen fusion shutoff down the street at Sol, it struck me that maybe the incentives for galactic exploration might be re-framed. It is not so much a matter of whether galactic collision is literal in terms of stars or whether we will be around on a habitable Earth by then – or the two calamities will be actually occur at the same time – it’s just that the incentives for galactic exploration or expansion for an unknown intelligence ( or even ours) might not be simply to cover all the space possible as soon as one gets out of bed.
In the extreme case of robotic survey targeting, if the results can be sampled rather quickly lot ( e.g., lot sample polling prior to election), then the robotic probe effort might be too small to notice from a distance.
And then, on the other hand, ET’s might turn out to be super sloths.
If stellar system conditions are no longer conducive to pleasant living or the path around galactic center makes a serious wrong turn, then the ET sloths pick up an on an offer that they cannot refuse and migrate to another star. E.g., the increased population in the vicinity,
Our consideration of ET distributions in this or other galaxies is a little biased by our anticipation of observing them. So, consequently we dream up the most expansive minded ETs we can with some extrapolation about our own technological possibilities. Even here though, motivational psychology has to be considered. And the operative assumption is that ET would behave like a guest ( invited or not) to a wedding reception that would take up all the chairs.
Seeking temporary cover might suffice.
It is true that at times in human history, when a land bridge or a sea expedition bridged a gulf, there was a proliferation of human settlement over a continent or a region with large consequences.
But with closer examination we discover instances where landings on
far shores resulted in little or small change to the environment or societies already there.
Unless they all live underground or the concept of cities are alien to them, let us search for the lights of ETI urban areas…
https://www.space.com/alien-life-seach-city-lights-exoplanets?utm_campaign=58E4DE65-C57F-4CD3-9A5A-609994E2C5A9
https://vimeo.com/ondemand/alifeswork?fbclid=IwAR1S5vx7UaZqdmVfx2yiqw-Oh4yjc-7ArViouLHw4wlFZq89dkiEF_HEYw4&utm_content=bufferb392c&utm_medium=social&utm_source=linkedin.com&utm_campaign=buffer
A LIFE’S WORK: A Film About Taking the Long View – Now Available on Virtual Cinema!
from First Run Features PRO on April 16, 2022
Genres: Documentary
Duration: 1 hour 30 minutes
Subtitles: English
Availability: Worldwide
First Run Features presents “A LIFE’S WORK” on Virtual Cinema. When you buy a ticket, 50% of the proceeds go straight back to the venue or organization to support them during this difficult time.
What’s it like to dedicate your life to work that won’t be completed in your lifetime? Fifteen years ago, filmmaker David Licata focused on four projects and the people behind them in an effort to answer this universal question.
The subjects include Jill Tarter, Director of the SETI Institute, who has been involved in the search for extraterrestrial intelligence since the 1970s; David and Jared Milarch, father and son tree farmers and co-founders of the Champion Tree Project, who clone old-growth trees to combat climate change; gospel music archivist Robert Darden, who founded the Black Gospel Music Restoration Project, an organization that is trying preserve at-risk recordings from the black gospel music tradition; and Paolo Soleri, controversial architect behind Arcosanti, a town designed to test his theories about housing an overpopulated planet.
We discover what inspired them to begin, what obstacles they face, what drives and sustains them, and how they measure success of an endeavor they will not live to see completed. But most of all we discover that their lives really aren’t that different from everyone else’s: who hasn’t gazed at the stars and wondered if we are unique, nurtured a plant, sought ideal shelter, fell in love with a song and couldn’t wait to share it with someone? And who among us will truly see our work finished before we leave this earthly plain?
“In a time of when many of our rewards are instantaneous, it is mind boggling to be reminded that there are people who spend their lifetime patiently working on years long projects that they will not see finished. David Licata expertly tells the story of four of those unique individuals. A Life’s Work is a welcome a reminder of other ways of being in the world.” -Jim Robbins, New York Times science writer & book author
“A Life’s Work is a remarkable journey that reveals the minds of people willing to devote themselves to a cause far bigger than they are. A moving, heartfelt, and important lesson and inspiration for us all.” -Paul M. Sutter, PhD, Author of Your Place in the Universe & How to Die in Space: A Journey Through Dangerous Astrophysical Phenomena
A documentary by David Licata
90 minutes, color, 2021
Optional English Subtitles