A growing interest in JPL’s Solar Gravitational Lens mission here takes Wes Kelly on an odyssey into the past. A long-time Centauri Dreams contributor, Wes looks at the discovery of gravitational lensing, which takes us back not only to Einstein but to a putative planet that never existed. Part II of the essay, which will run in a few days, will treat the thorny issues lensing presents as we consider untangling the close-up image of an exoplanet, using an observatory hundreds of AU from the Sun. Wes has pursued a lifetime interest in flight through the air, in orbit and even to the stars. Known on Centauri Dreams as ‘wdk,’ he runs a small aerospace company in Houston (Triton Systems,LLC), founded for the purpose of developing a partially reusable HTOL launch vehicle for delivering small satellites to space. The company also provides aerospace engineering services to NASA and other customers, starting with contracts in the 1990s. Kelly studied aerospace engineering at the University of Michigan after service in the US Air Force, and went on to do graduate work at the University of Washington. He has been involved with early design and development of the Space Shuttle, expendable launch systems, solar electric propulsion systems and a succession of preliminary vehicle designs. With the International Space Station, he worked both as engineer and a translator or interpreter in meetings with Russian engineering teams on areas such as propulsion, guidance and control.

by Wes Kelly

Part 1. “Each of the Known Suspects Has an Alibi Related to His Whereabouts.”

[This article originated with an inquiry from our local astronomy club for a talk during an indoor meeting anticipating a cloudy sky.]

Among topics arising on Centauri Dreams, reader response often turns to investigation: the original scientific reports plus surrounding evidence, the basis for many of the website’s entries. And when a topic is unfamiliar or on a frontier of knowledge, reader investigation can be a matter of playing catch up, as I can attest. Fair enough. Scientific observations, data interpretations or hypotheses… Take the matter of heading out to deep space to collect light from the other side of the sun and then deconvolute it to extract the image of an exoplanet. The steps to this objective have to be judged individually or reviewed as stepping stones, connecting lines of inquiry… Or maybe going so far as to say, “All right. Now let’s just start all over…”

So, I did. With the result an attempt at integration, or else a short story.

And to what conclusion am I drawn? That there is significant linkage between the proposed solar gravitational lens (SGL) telescope to be placed out at 550 AU distance and (Envelope, please…) the planet Vulcan.

The one from which the Starship Enterprise first officer supposedly arose? The logician with a name spelled like a noted 1960s contemporary pediatrician? No, that is just a ruse, “to cloud men’s minds”, an inhabitant of a fictitious exoplanet. The one of concern here I first heard of before Gagarin took off from Baikonur. It was in some science fiction anthology at the local library or bookmobile. I can’t recall who wrote it, but it was probably an anachronism by the time it went to press in the pulp magazines originally, at least a decade or two before a Redstone rocket was launched. And as a grammar school kid, I never finished it. A piloted trip to a planet inside Mercury’s orbit was an imaginary rabbit hole into which I was either unwilling or not patient enough to complete the full dive. Nor evidently did Einstein biographer Abraham Pais, in which I thought all things related to Albert would reside in his book, Subtle is the Lord…” [1]. I see no reference to Vulcan in his index.

In a less cynical era, I remember a spoken introduction to discoveries reported in the news. It was communicated on long train or bus rides or standing in an interminable queue, the oft optimistic assertion that there existed a benign, secret, scientific conspiracy (something Sir Arthur Conan Doyle might have joined or devised) to make life better for everybody. Largely, or at least not universally, since sometimes, some party might view a word-of-mouth development as the business end of a new and special gun barrel. More likely though, the secret org would have to get back with us much later – if at all. But whatever the development was, and if it coincided with a continuing concern, the reader, radio listener or TV news watcher could feel obliged to come up to speed on the subject. Since that halcyon era despite the changes in media… “Do you know what they are doing now?” …

Plus ça change, plus c’est la même chose.

As an engineer with a classical mechanics background, shunning issues of electro-magnetism or general relativity but interested in astronomical developments all the same – and especially for the past several decades, those related to exoplanets, I’ve climbed over such obstacles anyway. And on the issue of the field of view for a GR telescope looking backward toward the sun reliant on some convolution to see an exoplanet, I got stuck like a donkey with a cart. In an earlier article for Centauri Dreams [Archive, A1], I gave an account of those pursuits, of examining what became known as habitable zones (HZ) around binary system stars, converting terrestrial trajectory tools I had been using for more sundry inquiries to address that distinct celestial 3- body problem. This was at about the time in the 1980s when no exoplanets were known of anywhere. So, to some degree, it was all in fun. Alpha Centauri looked more promising for stability than Procyon, and Procyon better than Sirius – which was terrible. Beta Pictoris, back in those days had a circumstellar disk of dust according to the Infra-Red Astronomical Satellite (IRAS) of that era. Just maybe something could be forming in the midst of it.

So, here we are decades later. The James Webb Space Telescope was in development for so long, that it too in conception had preceded the discovery of exoplanets; but its remarkably wide aperture for a space telescope and its IR sensitive instrumentation, originally loaded aboard for cosmological questions, adapted very well to follow-up investigations of a host of exoplanets in its visual and near IR bands. These objects were discovered by other instruments in space or on the ground; detected indirectly at first through stellar radial velocity spectral shifts, then stellar transits, primary astrometric shifts in a few cases, a couple of direct images by the Hubble Space Telescope and so forth.

If one checks the JWST website [2] and its observing schedule, exoplanet observations entail a large fraction of the space telescope’s time. Not necessarily the search for new ones, but definitely follow-up campaigns initiated at other observatories: Kepler and TESS space telescope transits, stellar radial velocity cases obtained from large ground-based observatories on mountain tops or high desert plateaus, and the astrometric detections obtained from the Hipparcos and Gaia space telescopes for stars that possess periodic oscillations against the celestial background.

As for exoplanet detections based on gravitational lensing, I suspect that JWST’s “hands” are largely tied since one needs literally an alignment of the planets and stars. This last mysterious concept – relativistic micro-lensing as practiced thus far – appears to give an exoplanet population sampling. A survey technique that penetrates deeper into this galaxy and local ones than would be possible if light were not bent and magnified by stars very close to the line of sight, often also producing a ring effect around a gravitational mass. In many cases, light of distant objects such as galaxies and star clusters deeper in space can be extracted from distorted images such as annular rings, no mean feat of transformation and data processing itself. An image is distorted or convoluted and applied mathematical formulas “deconvolute” them – if they can. But now, there is the possibility of applying these last-mentioned features and techniques to scrutinizing specific exoplanets, ones that are selected and not the luck of the draw.

How did this state of affairs come about? Well, we can start with the planet Vulcan. If we consider this hypothetical planet for a few moments, then General Relativity seems a little less miraculously sprung from Olympian brows. But whether you are thinking of the exoplanet home of Star Trek’s Spock or the planet on an inside track with respect to Mercury, in both cases we are dealing with phantoms. Note that planet Vulcan’s parameters do not appear in Table-1.

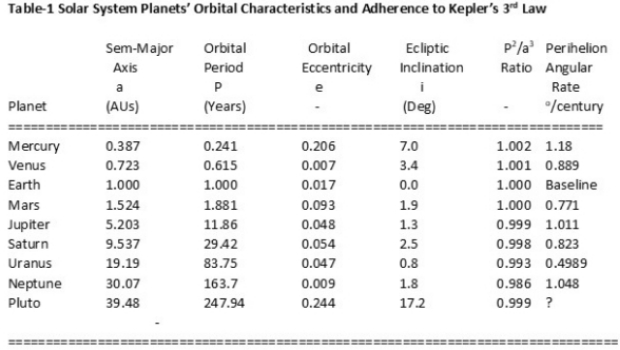
Table-1. Orbital properties of planets Mercury through Neptune (+ Pluto) in terms of their semi-major axes in Astronomical Units, periods in Earth years and orbital eccentricity. The second to last column, using these normalized terrestrial units of the first two columns, shows how closely they adhere to Kepler’s 3rd law: that an elliptical path around the sun has a constant proportion of period squared over the semi-major axis cubed. It is tempting to say radius squared, thinking of planets as near circular. But semi-major axis (as shown in Figure 1) governs calculation of average orbital velocity about a circumferential distance (v = 2 ? a / P). The last column, argument of perihelion advance in degrees per century, figures into the later part of our story. Pluto, whether true planet or not, should be included too for its perturbed P²/a³ value since it bears on searches for “Planet X”. And Mercury’s did once too for another putative planet.

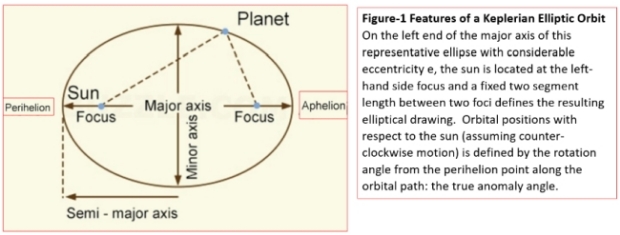
As Table-1 and Figure 1 show, the motion that Kepler discovered is a fascinating example of three defining equations based on conservation of energy, conservation of momentum and the conic, defining an orbit in a 2-body system and on a plane. Johannes Kepler’s laws related directly to planets in planes occupied by the sun at a focal point as well. But the planets did not all exactly, or even necessarily, share the same plane – so long as the sun’s location occupied one common focal point shared by all of them. There were differences enough in the planets’ planar geometries so that their celestial coordinates have to be defined by additional elements beside semi-major axis, eccentricity and position of perihelion with respect to a single demarcation on the orbital plane such as the Earth-based ecliptic. To name some of the conventions used, there is the inclination of the orbital plane with respect to the ecliptic plane as a reference plane, the argument of the perihelion in terms of angular passage through that plane, and then the rotation of the plane about the sun in the reference plane with respect to a reference line (in the direction of constellation Aries) – the angle of the ascending node (See Figure 2).

Now if we had true Keplerian motion about the sun and a disregard of Newtonian mechanics, these values would remain immutable. But they don’t remain so. Due to the masses of the planets relative to the sun, there is a center of mass of the solar system, and when planets approach each other, they alter their paths as a first order “Newtonian” effect. So, not only do the orbital elements mentioned above have specific values, but they change over time, cyclically narrow in some cases such as eccentricity, or else with a complete rotation of features like the ascending node of a planet on the ecliptic plane, or the angular position of the perihelion with respect to that same ecliptic plane, rotating 360 degrees eventually. These parameters could be completing a revolution over centuries or millennia. And not always at the same rate, because with eight principal planets, their relative positions and resulting attractive forces are complex over time. Still, based on records kept back to Mesopotamian days, planetary perturbations of the Newtonian variety can be taken into account. But with closer and closer scrutiny beside the first order effects, in at least one case a secondary effect can be isolated as well. The polynomial approximations of the change of orbital elements with time are known as planetary ephemerides [3].

Figure-2 An Elliptical Orbit in Three-Dimensional Space

Secondary effects do need to be accounted for. If for nothing else, back in the 19th century, to obtain accurate nautical almanacs for marine navigation. [In one volume of the Patrick O’Brian series about the Napoleonic Wars, Captain Jack Aubrey was telling anyone who would listen about his sightings and time recording of the Galilean moons to determine his seaborne longitude.] So, one could ask, like Sherlock Holmes, one of 19th century’s most luminous fictional investigators, “These position discrepancies, what could account for this?”

Table-2 The four above forms served to identify ~5000 distinct and repeatedly observed exoplanets thus far, providing orbital elements (partial or complete), in some cases, masses, surface temperatures, some chemical components. The fifth procedure’s service has been of a more fleeting nature, a keyhole into deeper space as a result of light bent and magnified by a gravitational field in the line of sight. On the other hand, if the proposed gravity lens telescope is installed as described, astronomy is set on a path toward learning relative minute details about what exoplanets it is able to target.

In the studies I mentioned of planets in binary star systems, the stable exoplanets would have very accentuated changes in eccentricity, periastron position or ascending node. Illustrative but too large in some cases, and the system breaks down into chaotic motion in which a planet could be ejected or graze a sun. Interesting in its own way, but this did not shed any light on relativistic effects, though I did have an opportunity to connect them one day. Toward the end of such hobby studies, I found that one of my work colleagues was pursuing his Ph.D. with a general relativity focus in his dissertation. We discussed the advance of argument of perihelion one day – and I explained that I had noted such behavior even with the sun and Jupiter affecting a third body such as Earth or Mars. It looked to me that it was about the right order. Sonny White agreed in a sense. He said that that was “about” right. Close, to some order, to what was seen in tables. But the famous relativistic effect observed with Mercury was an additional but slighter perturbation to the planet’s path. Remarkably, nineteenth century astronomers could distinguish this additional effect and, even in the absence of electronic computing, frequently fretted over it.

[*Before going Relativistic in this discussion, beside third bodies in Newtonian examinations of orbital motion, another source of disturbance from Keplerian motion worthy of note is in the subtle departure from spherical distribution of mass in the principal body around which another orbits, in particular from “oblateness”, the flattening of a spherical body so that the polar diameter is shorter than the equatorial. This too causes advances of the ascending node or the periapsis. For low earth orbits such as space stations, depending on their inclination, it could be 8 to 5 degrees per day in the fixed celestial sphere for the ascending node with inclinations between 28.5 and 51 degrees and circa 300 to 400-kilometer altitude. More massive and more oblate objects cause a faster rate. For Jupiter it would be about ten times faster using the same altitudes and inclinations. Compact, dense objects such as white dwarfs, neutron stars and black holes can experience rotational rates sufficient to engender oblateness and excite even faster advances. And yes, even in the case of the sun with its fluid volume and flattening. From time to time there are efforts to isolate the sun’s contribution to precession, e.g., [9]. However, we should note that Mercury does not skim the surface of the sun like space station examples above the Earth, Jupiter or condensed objects as mentioned above.]

Now when it came to planets, in antiquity and even up to Kepler’s time, one could say that there were “about” five genuine planets. Seven if you take into account eras or societies that were still debating whether an Evening and Morning Star could really be the same orb and then designated them as Venus or Mercury. Things stood about there until after both Kepler and Newton were gone. A number of mathematical astronomers, especially in France, observed departures from the Keplerian motion, to be sure. And in the case of Neptune, it was predicted before it was discovered with inferences gathered from its neighbors.

Verifying the Outer Planet discoveries, I note that William Herschel first observed Uranus (number 7) in March of 1781 and identified it as a planet. Quite a leap considering the intellectual inertia against such a premise until then.

Moreover, astronomers from the time of Hipparcos and Ptolemy with the Almagest charted “stars” where Uranus should have been when the observations were made. With good seeing conditions it can be visible to the naked eye. But the number of planets might have become a facet of natural science in Ptolemy’s time as well*. While studying Jupiter’s moons, Galileo had written Neptune into his own star charts, but this did not constitute its discovery. Rather, it was the other way around when 20th century astronomer Charles Kowal checked Galileo’s 17th century charts and found it there too, noted over a century before the genuine discovery event and then identified a century and a half after it was already noted as a planet.

[*The mental bias of having five planets wandering the sky for many centuries had a number of social features. Mythology and name designations in the sky seemed to complement each other. What allegorical role would a newly discovered planet assume if the mythic and astrological principal roles had already been taken? ]

Neptune’s discovery, however, was an event distinct from that of the seventh planet’s discovery process and a pivotal event in our story. In 1821, Alexis Bouvard published astronomical tables of the orbit of Uranus. Subsequent observations revealed substantial deviations from what the tables extrapolated, leading Bouvard to hypothesize that an unknown body was perturbing the orbit through gravitational interaction. In 1843, John Couch Adams began work on the orbit of Uranus using what data he had to point to a Planet 8, much of it supplied by Sir George Airy, the Astronomer Royal for Great Britain. Mathematical labors over 1845–1846 produced several different estimates for a new planet’s characteristics.

So, that was what was going down on one side of the English Channel or La Manche; this was what happened on the other. During 1845–1846, Urbain Le Verrier, independently of Adams, developed his own calculations but obtained little follow-up locally in France. But still, Le Verrier’s first published estimate of the planet’s longitude and its similarity to Adams’s estimate, caused some concern to Astronomer Airy that this search for an eighth could turn into a true horse race. Le Verrier grasped this too and then sent a letter urging Berlin Observatory astronomer Johann Gottfried Galle to search with the facility’s refractor.

“On the 23rd of September 1846, the day Galle received the letter, he discovered Neptune just northeast of Iota Aquarii, 1° from the “five degrees east of Delta Capricorn” position Le Verrier had predicted it to be, about 12° from Adams’s prediction, and on the border of Aquarius and Capricorn according to the modern IAU constellation boundaries.”

For our story, the issue is not whether it was Adams or Le Verrier who correctly calculated the position of an unknown planet, but the fact that it was beginning to become both demonstrable and fashionable. Also, in the telling of new planets discovered, if the story is followed close enough, one notes that Uranus was not predicted; instead, it was detected by observation or surveying the night sky. The game of new planet search and discovery continued in the outer solar system because Neptune had irregularities in its motions too. But discovery of Pluto weighed in insufficiently to explain this gas giant’s deviations from its presumed Newtonian path.

So, that was the situation mid-19th century moving out from Earth’s orbit among the “superior” planets, capable of unlimited azimuths above the sun as viewed from Earth. Now what about the situation with the other two, tracking interior to Earth’s orbit, Venus and Mercury? The ones with limited elongation from the sun.

Since Venus is the least eccentric of all the planetary orbits, it just might be that it is very difficult to see whether there is anything mysteriously moving its celestial longitude of perihelion any faster than it should. Yet actually I am aware of one paper published in the US decades back addressing this problem. Examining it one day, I noticed as well that the author had assumed an order of magnitude larger Venerian eccentricity than stated elsewhere. A virtuoso performance otherwise. However, the neighbor of Venus sunward indeed has eccentricity and inclination only rivaled by Pluto. And one does not have to wait 240 Earth years for a cyclic update; just 88 days. As a result, this was where the orbital number crunchers of the mid-19th century next turned their guns, a problem for which the astronomical practitioners of classical mechanics could roll up their sleeves: By their reckoning, the irregularities in Mercury’s motion needed explanation by the perturbative influence of a yet undiscovered innermost planet. And it became a now largely unknown namesake for the exoplanet home of Star Trek first officer Spock: the planet Vulcan.

It is often noted (e.g., with regard to UFOs) that it is near impossible to prove a negative; i.e., that an object or a phenomenon does not exist in some figurative dark woods. But demonstrations of existence do not always end happily either. In fact, the phantom planet Vulcan, the search target of many, was supposedly discovered by some. Buoyed by successful discovery of Neptune, Urbain Le Verrier was among those engaged. Even before Neptune’s discovery, despite what was said above, sightings of a planet interior to Mercury had occurred, practically since Galileo’s time. Likely, if anything they were sunspots. But Le Verrier’s success with Neptune now fueled 19th century observation campaigns around the world.

At the request of the Paris Observatory, Le Verrier in 1859 published a study of Mercury’s motion based on position observations of the planet and 14 solar transits. Discrepancies in observation vs. theoretical modeling remained; to the effect that its perihelion advance or precession was slightly faster than had been surmised. The observed value exceeded the classical mechanics prediction by the small amount of 43 arcseconds per century. Some unidentified orbiting object or objects inside the orbit of Mercury; either another Mercury sized planet or an unknown asteroid belt near the Sun could be responsible, the mathematical heirs of Lagrange and Laplace had concluded.

Sun or Son of Vulcan?

Emerging from a flock of observers reporting no success, amateur astronomer Edmond Modeste Lescarbault had searched for transits from 1853 to 1858 and thereafter more intently. He contacted Le Verrier in 1859, reporting a solar transit of the suspected planet on 26 March of that year observed from his home 70 kilometers southwest of Paris. With some reservation, but evidently not enough, Le Verrier endorsed Lescarbault’s report and proposed before the French Academy that the planet’s name be Vulcan. Lescarbault was elected to the French Legion of Honor. From calculations, Le Verrier described Vulcan thus: In circular orbit about the Sun at a distance of 21 million kilometers or 0.14 AU with a period of 19 days and 17 hours and inclination to the ecliptic of 12 degrees and 10 minutes. Seriously and specifically. As seen from the Earth, Vulcan’s greatest elongation from the Sun would be 8 degrees or about 16 solar diameters. This is worth remembering in what will follow.

Since we have noted a long full stop in discovering planets after evening and morning stars were unified into single entities, we have perhaps given mixed signals about inner or inferior planet calls of discovery, mostly since Galileo’s time and the use of the telescope. Sunspots were discovered and monitored shortly after Galileo’s astronomical reports. They had some tendency to wander, disappear or reappear, but they also indicated the rotation rate of the sun’s surface, about thirty days. Note that Le Verrier’s object orbits the sun quicker than the sun rotated still 0.14 AUs out and it was presumed to have an inclined path, but not as large as Mercury’s. At the very least, his solution distinguished itself from a sun spot.

There were many attempts to confirm the discovery, of course, and among efforts tending to confirm were those conducted by newcomers to this European sweepstakes, observatories in the United States. A team at the University of Michigan (1878), for example, obtained a positive. California’s Lick Observatory and other groups observed solar eclipses in 1883, 1887, 1889, 1900, 1901, 1905 and 1908 with no joy. Note about when this mostly fruitless search effort stopped?

A century or so after this campaign, our selective memories tend to suggest that Albert Einstein’s solution to Mercury’s odd behavior was an answer to a question that was never really asked. Yet it appears to be the contrary, a significant scientific issue; like say, a century later, where were all those neutrinos that the sun was supposedly producing in its core? And once Einstein tossed an explanation, over the fence, the scientific investigative process shifted its focus: “OK. We see what you are saying. Now how do we go about testing that?”

Vulcan as result slipped off the astronomical stage. Solar eclipses would no longer provide shade to search for a close-by planet, but for observing celestial position shifts of emerging starlight. Steamer tickets to remote sites for solar eclipses did not diminish. Now there was a different and perhaps more compelling motivation. Einstein was saying more and more about the strange properties of space, mass and time. There were several opportunities to test this, but the solar eclipse of 29 May 1919 turned out to be crucial. The Hyades constellation was near the ecliptic plane and a couple of stars seemed apt

Commanding General of Relativity?

Cambridge University astronomer (Sir) Arthur Eddington was not known from birth as an expert on General Relativity, but by the 1920s he was something of a GR phenomenon himself. There was a quote then in the English-speaking world that the only two individuals who understood the concept were Albert Einstein and Eddington, his English interpreter. Perhaps it originated with upper-level physics students remarking such to their juniors over lunch or in Cambridge halls. Better that than “General Relativity” Eddington, which surely would have provoked his ire. It should be noted that along with the post-war eclipse expeditions, Eddington was among the first to attribute sun energy reserves over geological epochs to hydrogen fusion and other nuclear reactions in its core. It was in answer to the enigma of how Earth’s geology suggested formation eons ago and stable heating since.

Eddington was also one of the few eyes and ears Great Britain had on science developments across the trenches of World War I; partly the result of his Quaker pacifist background and principles, partly due to Cambridge University’s efforts to retain him in its research community. On the continent Dutch physicist Willem de Sitter had communicated to Eddington in 1916 about Einstein’s work – and Eddington ultimately suggested to Einstein that he use his theory to calculate an answer to Mercury’s precession rate. Thus, in the English-speaking world in the 1920s no one was better situated to write about General Relativity. Except maybe Chandrasekhar. But that would be later; after a fitful period of work together at Cambridge. I referred back to a biography of Chandrasekhar [6] read a decade back for background not obtained on the 1919 GR test in the Pais biography of Einstein. And there was something right away. Chandra maintained Eddington’s selection to lead the expedition was not out of deference for a GR specialist, but pique over his WWI deferment from the general conscription (page 8) of the recent war.

Or, perhaps this reflected instead little faith for a successful outcome, or that this particular hypothesis held much of a future for physics. Ultimately, among Chandrasekhar’s many works was a biography of his mentor published in 1983 [7]. I look forward to obtaining it.

Einstein’s General Relativity propositions had already instigated previous efforts to observe stars in solar eclipse vicinity. A German effort arrived on station in Tsarist Russia (the Crimea) with unfortunate August 1914 timing; and then the group was held in detention, leaving finally with no results. After the war, opportunities to observe would appear; one along a track over the South Atlantic – if weather would allow. In fact, seeing conditions and equipment at both sites where Eddington’s teams set up camp (Principe’ Island off West Africa and Sobral in Brazil) were questionable at best and the initial results were regarded skeptically though the phenomenon passed the test of time.

Figure-4. The experimental geometry that the solar eclipse provided was an opportunity to observe light emitted from a star of known position in the celestial sphere as it reappeared from behind the shining obstacle of the sun and the shadowing of the moon in a total solar eclipse.

Three possible results one could hypothesize based on the nature of light (i.e., photons moving at the speed of light but with no mass). Were photons akin to comets (which have mass) as they passed the sun at perihelion, they would be bent in a hyperbolic orbit. That’s one possibility (1). And if that were the case, then how could that be reconciled with the constant speed of light in a vacuum? [There was spectral shift to the red, however.]

But since the photons are assumed to have no mass, perhaps their paths would not be bent at all? That’s another (2). Struggling with the basics of physics in first year or later, I could see how such an outcome could strike one as just fine.

And then there was Einstein’s formulation of the space time continuum that had been in development over a decade (3). Einstein’s prediction was not a hyperbolic path, but it is bent based on its closest passage to the sun, the sun’s mass ( or that of any other possible perturbing object)…

A bend angle from the normal stellar line of sight (LOS) would be

?? = 4 GM/c²b,

where G is the universal gravitational constant, M is the mass of the sun, c is the speed of light and b is the closest light ray approach (distance) to the sun’s center, effectively the solar radius, in this case. Were it a conic, it would be perihelion. If, for example, we use Jupiter as a lens (r_J/r_S ~ 1/10, M_J/M_S ~ 1/1000), the deflection is about 1/100th the magnitude.

Since b is the only variable called out for the sun, other masses (M) would give different angles for the corresponding distances. Although this formula is approximate, it is accurate for most measurements of gravitational lensing, due to the smallness of the ratio r_S/b, with r_S the radius of the sun. If b is less than the r_S value, we can presume that the light is blocked, unless some stellar light band can penetrate the solar medium. Larger, and the angle of deflection falls accordingly.

For light grazing the surface of the sun, the approximate angular deflection is roughly 1.75 arcseconds. This is twice the value predicted by calculations using the Newtonian theory of gravity. It was this difference in the deflection between the two theories that Eddington’s expedition, other 1919 ventures, and later eclipse observers would attempt to observe.

Well, if not simply Eddington’s, measurement of subsequent solar eclipses verified the stellar light deflection. And a first reaction to this news now might be like that of an observer of a shell game: “But what does this have to do with the orbital elements of Mercury?” A fair question. For our purposes it was confirmation of an overall theory that explained adjustments to Newtonian dynamics which affected both bodies of mass and massless particles in space. Space was warped by mass and energy and the tensor-based formulations of General Relativity accounted for both Mercury and the starlight during observed in eclipse. In math hierarchy tensors can be considered either as a more complex form of matrices and vectors or else the overall nomenclature of math forms of which matrices and vectors are of a simpler form. Beside general relativity, engineering applications include fluid mechanics and elastic solids in mechanics experiencing stress or loads. In workbooks such as Schaum’s Outline example problems are usually provided for all three applications. During the decade prior to the eclipse, one could say that Einstein worked such problems for himself and then with the aid of several European mathematicians. It was perhaps provident for all that several early eclipse expeditions were rained out, allowing Einstein to derive his best and final answer.

Across the Atlantic in the United States, Moulton’s well-known text on celestial mechanics went into its revised second edition [4] in 1921. It contains derivations and historical descriptions of many classical celestial mechanics problems; how they were solved. Included are many references to Le Verrier’s work, but not to the Vulcan episode. As well as I can reconstruct from this and other sources, Le Verrier might have used a technique developed by Gauss for the Vulcan study. On page 4 of Moulton, Einstein and the so-called Principle of General Relativity are discussed in the introduction’s section 5, concerning the laws of motion: “The astronomical consequences of this modification of the principles of mechanics is very slight unless the times under consideration are very long, and whether they are true or not, they cannot be considered in an introduction to the subject.”

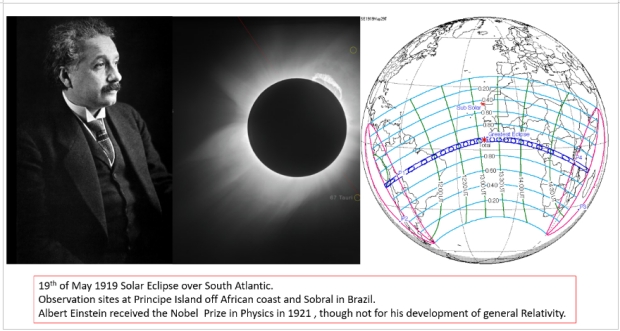
Figure-5 Albert Einstein, the Eclipse and its Track across the South Atlantic for 19 May 1919.

At this point, having one’s hands on an all-around deflection angle for light at the edges of a “spherical lens” of about 700,000 kilometers radius (or b equal to the radius of the sun r_S), if it were an objective lens of a corresponding telescope, what would be the value of the focal length for this telescopic component expressed in astronomical units?

The angle of 700,000 km solar radius observed from 1 AU, gives an arcsine of 0.26809 degrees. This is consistent with the rule of thumb solar diameter estimate of ~0.5 degrees.

Expressed in still another way, solar radius from this arcsine measure is 965 arc seconds. When the solar disc itself is observed to be about 1.75 arc seconds in radius, that’s where you will find the focus for this objective lens.

If we take the ratio of 965 to 1.75, we obtain a value 551.5. In other words, a focal point for the relativistic effect at 551.5 AU’s out. Thus, the General Relativity effect implies that light bent by the sun’s gravity near its surface radius is focused about 550 AUs out from the sun. And like the protagonist of Moliere’s 16th century comedy, as I run off to tell everyone I know, I discover a feeling akin to, “For more than forty years I have been speaking prose while knowing nothing of it.”

This could be a primary lens for a very unwieldy telescope. True, but not unwieldy in all manners. When we consider the magnification power of a telescope system, we speak of the focal length of the objective lens over that for an eye piece or sensor lens focal length. And habitually one might assume it is enclosed in a canister – as most telescopes sold over the counter at hobby stars are. But it is not always necessary or to any advantage. Consider the largest ground-based optical reflectors, or the JWST and radio telescopes. Their objective focal lengths extend through the open air or space. The JWST focal length is 131.4 meters or taller than its Ariane V launch system. Its collected light reaches sensors through a succession of ricochets in its instrumentation package, but not through. a cylindrical conduit extending out from the reflector any significant distance to the front. [Note: The Jupiter deflection case mentioned above would make the focal length 100x longer.]

From this point on, our relation with General Relativity will have a “special focus”, when we discuss some aspects of operating this telescope with a spherical lens in Part II.

References for Part I and II

1.) Pais, Abraham, Subtle is the Lord … The Science and Life of Albert Einstein, Oxford University Press, 1982.

2.) https://www.stsci.edu/jwst/science-execution/observing-schedules

3.) Vallado, David A., Fundamentals of Astrodynamics and Applications, 2nd edition, Appendix D4, Space Technology Library, 2001.

4.) Moulton, Forest Ray, An Introduction to Celestial Mechanics, 2nd Edition, Dover, 1914 Text.

5.) Taylor, Jim et al. Deep Space Communications, online at https://descanso.jpl.nasa.gov/monograph/series13_chapter.html

6.) Wali, Kamshwar, C., Chandra – A Biography of S. Chandrasekhar, U. of Chicago Press, 1984.

7.) Turyshev et al., ”Direct Multipixel Imaging and Spectroscopy of an Exoplanet with a Solar Gravity Lens Mission,” Final Report, NASA Innovative Advanced, Concepts (NIAC) Phase II.

8.) Helvajian, H. et al., “Mission Architecture to Reach and Operate at the Focal Region of the Solar Gravitational Lens,” Journal of Spacecraft and Rockets, American Institute of Aeronautics and Astronautics (AIAA), February 2023, on line pre-print.

9.) Xu, Ya et al., ”Solar oblateness and Mercury’s perihelion precession”, MNRAS, 415, 3335-3343, 2011.

A1.) Archives: In the Days before Centauri Dreams… An Essay by WDK (centauri-dreams.org)

A2.) Archives: A Mission Architecture for the Solar Gravity Lens (centauri-dreams.org)

End Part I