Looking at the latest work from Carnegie’s Alan Boss reminds me once again of the crucial role computers play in astrophysical calculations. We’re so used to the process that we’ve come to take it for granted, but imagine where we’d be without the ability to model complex gravitational systems. To understand planet formation, we can simulate a protoplanetary disk around a young star and let a billion years pass in front of our eyes. And as our models improve, we can set the process in motion with ever greater fidelity.
Read Caleb Scharf’s The Copernicus Complex ( Farrar, Straus and Giroux, 2014) to see how much we’ve learned by ever more precise modeling. Back in the late 1980s, Jacques Laskar (Bureau des Longitudes, Paris), Gerald Sussman and Jack Wisdom (the latter two at MIT) developed mathematical approaches that could track changes to orbital motions to understand our solar system’s past. Their work and the wave of innovation that followed helped us understand exponential divergence over million-year time periods, a crucial factor, as Scharf shows, in how unpredictable planetary motions can be:
Newton’s physics and its application by scientists like Laplace had appeared to be describing a clockwork universe, a reality based on laws that could always lead you from point A to point B, through space and time. And although the concepts of chaos and nonlinearity were well-known by the time these numerical computer experiments were carried out on planetary motions, this was the first real confirmation that our solar system was neither clockwork nor predictable.
In other words, when dealing with astronomical time-frames, we begin to find outcomes that could not have been predicted as we run our simulations. We’re observing chaos at play in complex gravitational systems, where tiny interactions can ultimately change the trajectories of entire planets. Scharf’s discussion of these matters celebrates the computer’s ability to model these phenomena and observe different results, but it’s also a humbling reminder of our limitations in thinking that with enough information we can always predict the outcome.
Learning How Stars Form
What Alan Boss is modeling is the formation of stars, using three-dimensional models of the collapse of magnetic molecular cloud cores. His simulations depict the formation of stars as clusters of newly formed protostars come apart. What they show is that younger star and protostar populations have a higher frequency of multiple-star systems than older ones. In other words, many single-star systems like our own start out as multi-star systems, with stars being ultimately ejected to achieve stability. You can see the modeling at work below.
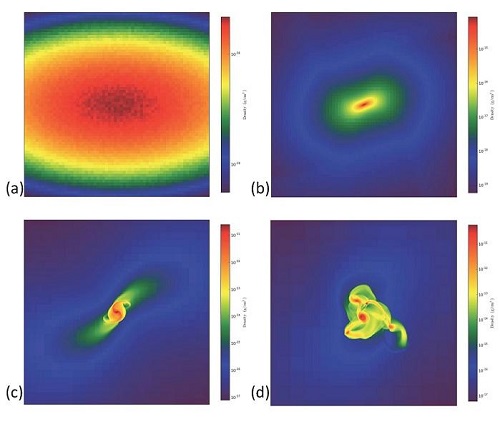
Image: The distribution of density in the central plane of a three-dimensional model of a molecular cloud core from which stars are born. The model computes the cloud’s evolution over the free-fall timescale, which is how long it would take an object to collapse under its own gravity without any opposing forces interfering. The free-fall time is a common metric for measuring the timescale of astrophysical processes. In a) the free-fall time is 0.0, meaning this is the initial configuration of the cloud, and moving on the model shows the cloud core in various stages of collapse: b) a free-fall time of 1.40 or 66,080 years; c) a free-fall time of 1.51 or 71,272 years; and d) a free-fall time of 1.68 or 79,296 years. Collapse takes somewhat longer than a free-fall time in this model because of the presence of magnetic fields, which slow the collapse process, but are not strong enough to prevent the cloud from fragmenting into a multiple protostar system (d). For context, the region shown in a) and b) is about 0.21 light years (or 2.0 x 1017 centimeters) across, while the region shown in c) and d) is about 0.02 light years (or 2.0 x 1016 cm) across. Credit: Alan Boss.
As the molecular cloud that will form a star collapses, how it fragments depends, Boss shows, on the initial strength of the magnetic field. If the magnetic field is strong enough, single protostars emerge, but below this level, the cloud begins to fragment into multiple protostars. From the paper:
The calculations produce clumps with masses in the range of ~0.01 to 0.5 M?, clumps which will continue to accrete mass and interact gravitationally with each other. It can be expected that the multiple systems will undergo dramatic subsequent orbital evolution, through a combination of mergers and ejections following close encounters, resulting ultimately in a small cluster of stable hierarchical multiple protostars, binary systems, and single protostars. Such evolution appears to be necessary in order [to] produce the binary and multiple star statistics that hold for the solar-type stars in the solar neighborhood…
Those statistics are striking. Roughly two-thirds of the stars within 81 light years of the Earth are either binary or part of multi-star systems. And because what we see today as single stars can also be the result of ejection from a multi-star system, the formation of binary and multi-star systems seems to be commonplace. I’m interested in these findings because if we are to understand our own place in the cosmos, we’re beginning to see that we have to account for why single-star systems do not seem to be the default in the Milky Way.
The paper is Boss and Keiser, “Collapse and Fragmentation of Magnetic Molecular Cloud Cores with the Enzo AMR MHD Code. II. Prolate and Oblate Cores,” in press at The Astrophysical Journal (preprint).



This bring to mind the Fomalhaut system with its surprisingly far spaced-apart companions. It would be interesting to speculate whether the Sun may have formed in a similar widely-bound system, with its companions being pulled apart over aeons.
In the future as we amass more data, my hypothesis is that it will be shown that widely-spaced systems are more likely to be quite young and we can expect that the Fomalhaut system billions of years in the future will become single stars.
“Scharf’s discussion of these matters celebrates the computer’s ability to model these phenomena and observe different results, but it’s also a humbling reminder of our limitations in thinking that with enough information we can always predict the outcome.”
It may not be clear that it is not possible to model the outcome by any conceivable model. What they generally do is to constrain the errors to some minimum value, and quantify that error, then run the model many times with slightly different initial conditions. They are sampling the phase space to establish the probabilities of various outcomes. For example, the probability that a planet or other body will be ejected from a system within some number of My. These “predictions” are limited by model precision and differences between the model and reality. Well, that and exogenous factors like a near pass by another star.
Hi Paul
Mentioning Alan Boss reminds me of his discussion of direct gravitational collapse as a planet formation mechanism. Simplistic models suggested planets would form very easily from a gravitationally unstable proto-planetary disk, but more elaborate treatments of heat-flow suggested fragmentation of a proto-planetary disk is quite difficult, with the over-densities being smoothed out too quickly.
Yet the multitude of Kepler planets snuggling up close to their stars poses the reverse problem – that the required disk would fragment much too easily if the planets were formed in situ, as discussed in this recent preprint: Formation of close in Super-Earths & Mini-Neptunes: Required Disk Masses & Their Implications
Migration of newly forming planets seems to be mandatory to produce most of the systems we know, including our own.
From the well behaved Galactic orbit that our sun follows, could we
say that:
1 ) proto-stars did not have much interaction with our sun’s formation.
2) the sun did not form near the center of it’s ‘birth’ cloud.
of course, there is a small probability that all of the above did happen
and sum total of the interactions put the sun into it’s current galactic orbit.
Maybe more detailed modeling will conclude that the sun was created off center of the it’s ‘birth’ cloud and maybe even at it’s edge which might explain the someway unusual structure of our solar system.
I am still a bit leery of accepting broad conclusions on planetary formation
from Kepler data. It is blind to smaller planets outside the tidal locking range of star and outward. We have no idea of how common they are.
Any interactions the young Sun had with any siblings seem a good way to explain the oddball objects out beyond the Kuiper Belt that comprise our relatively new designation of an Inner-Oort Cloud, such as the newly discovered VP113 ( http://www.planetary.org/blogs/emily-lakdawalla/2014/04020847-2013-fy27.html ). I wonder if any modelling has thrown any light on possible configurations that might’ve given us this Inner-Oort cloud?