Beamed propulsion has clear advantages when it comes to pushing a payload up to interstellar flight speeds, which is why Breakthrough Starshot is looking at laser strategies. But what about a neutral particle beam in conjunction with a magnetic sail? We’ve discussed the possibilities before (see Interstellar Probe: The 1 KG Mission), where I wrote about Alan Mole’s paper in JBIS, followed by a critique from Jim Benford. Mole, a retired aerospace engineer, is now collaborating with plasma physicist Benford (CEO of Microwave Sciences) to examine a solution to the seemingly intractable problem of beam divergence. Getting around that issue could be a game-changer. Read on for the duo’s thoughts on sending a 1 kg probe to a nearby star system with a flight time in the range of 70 years. Part 2 of this study, outlining engineering issues and the practical realities of cost, will follow.
by James Benford and Alan Mole
We advance the concept for a 1 kg probe that can be sent to a nearby star in about seventy years using neutral beam propulsion and a magnetic sail. The concept has been challenged because the beam diameter was too large, due to inherent divergence, so that most of the beam would miss the sail. Increasing the acceleration from 1000 g’s to 100,000 g’s along with reducing the final speed from 0.1 c to 0.06 c redeems the idea. Such changes greatly reduce the acceleration distance so that the mission can be done with realistic beam spread. Magsail-beam interaction remains an aspect of this concept that needs further study, probably by simulations.
Central features of Neutral Particle Beam Propulsion
Use of a neutral particle beam to drive a Magsail was proposed by Geoffrey Landis as an alternative to photon beam-driven sails [1]. Compared to beam-driven propulsion, such as Starshot, particle beam propelled magnetic sails, Magsails, substitute a neutral particle beam for the laser and a Magsail for the ‘lightsail’, or ‘sailship’. The particle beam intercepts the spacecraft: payload and structure encircled by a magnetic loop. The loop magnetic field deflects the particle beam around it, imparting momentum to the sail. The general ‘mass beam’ approach has been reviewed by Nordley and Crowl [2].
Particle beam propelled Magsails require far less power for acceleration of a given mass. There’s also ~ 103 increase in force on the sail for a given beam power. Deceleration at the target star is possible with the Magsail but not with a laser driven sail.
The neutral particle beam approach is conceptually similar to photon beams such as the laser-driven Starshot project. A disadvantage of reflecting photons from the sail will be that they carry away much of the energy because they exchange only momentum with the sail. Neutral particle beams transfer energy, which is much more efficient. The reflecting particles may in principle be left unmoving in space after reflection and thus the efficient energy efficiency can approach 100%.
The thrust per watt beam power is maximized when the particle velocity is twice the spacecraft velocity. The Magsail, with a hoop force from the magnetic field, is an ideal structure because it is under tension. High-strength low-density fibers make this lightweight system capable of handling large forces from high accelerations. The rapidly moving magnetic field of the Magsail, seen in the frame of the beam as an electric field, ionizes the incoming neutral beam particles. Nordley and Crowl discuss on-board lasers to ionize the incoming beam, although this adds additional on-board mass and power [2]. When the dipole field of the Magsail is inclined to the beam vector the Magsail experiences a force perpendicular to the beam vector, which centers it on the particle beam, perhaps providing beam-riding stability.
Ultrahigh Acceleration
Alan Mole proposed using it to propel a lightweight probe of 1 kg [3]. The probe was accelerated to 0.1 c at 1,000 g by a neutral particle beam of power 300 GW, with 16 kA current, 18.8 MeV per particle. The particle beam intercepts a spacecraft that is a Magsail: payload and structure encircled by a magnetic loop. The loop magnetic field deflects the particle beam around it, imparting momentum to the sail, and it accelerates.
Benford showed that the beam divergence is fundamentally limited by the requirement, at the end of the acceleration process, to strip electrons from a beam of negative hydrogen ions to produce a neutral beam [4,5]. Therefore neutral beam divergence is typically a few microradians. Mole’s beam had an inherent beam divergence of 4.5 µradians.
In Mole’s work, the neutral hydrogen beam at 18.8 MeV per particle and inherent beam divergence of 4.5 µradians accelerated to two-tenths of the speed of light (0.2 c) had acceleration of 103 g’s for 50 minutes [3]. This resulted in a 411 km diameter beam spot, far larger than the Magsail diameter, which was 0.27 km. So most of the beam missed the sail.
But if we use much higher acceleration, the sail will stay within the beam until it reaches the desired final velocity, even with microradian divergence. We choose 105 g’s, 106 m/s2 to accelerate to 0.06 c, 1.8 x 107 m/s.
Numerical experiments with the model developed by Nordley [6], and later replicated by Crowl, showed that the greatest momentum delivery efficiency is when the velocity of the neutral beam is twice the sail velocity. The physics of this is straightforward: Maximum energy efficiency comes when all of the energy goes to the sail and none of it remains in the beam. For a sail that is perfectly reflective, the beam bounces off the sail at the same velocity it impinges the sail. If after reflection it is moving at zero velocity (so none of the energy is left in the beam), the initial beam velocity must be twice the sail velocity, so that it impinges on the sail at a relative velocity equal to the sail velocity.
We take the beam velocity at the end of acceleration to be the twice the final sail velocity, 0.06c The energy of a hydrogen atom is imparted by accelerating through a voltage of 6.6 MeV. The mission parameters for a hydrogen beam then become those shown in Table 1.
The lighter the particle to be accelerated, the shorter the beam driver can be at a fixed field gradient. However, lighter-particle shorter beam drivers, while they may cost less, would require a larger sail due to the higher divergence of the beam.
For a second example, a mercury beam has a minimum divergence of 0.8 µradians, but must use far higher voltage because of the larger mass [4]. Mercury beam parameters are also given in Table 1.
Table 1 Parameters of neutral particle beam-driven sail probes
| Beam and Sail Parameters | Hydrogen Beam | Mercury Beam |
|---|---|---|
| Beam Divergence | 4.5 microradian | 0.8 microradian |
| Acceleration | 105 g’s=106 m/sec2 | 105 g’s=106 m/sec2 |
| Sail diameter | 1.46 km | 260 m |
| Sail final velocity | 0.06 c, 1.8 x 107 m/s | 0.06 c, 1.8 x 107 m/s |
| Acceleration distance | 1.6 x 105 km, 10-3 AU | 1.6 x 105 km, 10-3 AU |
| Acceleration time | 18 sec | 18 sec |
| Magsail mass | 1 kg | 1 kg |
| Kinetic energy | 1.6 1014 J | 4 1014 J |
| Beam peak power | 1.8 1013 W, 18 TW | 1.8 1013 W, 18 TW |
| Beam voltage | 6.76 MeV | 1.35 GeV |
| Beam current | 2.66 MA | 1.33 kA |
We will see that when the beam divergence is in reality roughly 3 orders of magnitude higher than previous studies have assumed, from a nanoradian to microradian, rapidly moves the beam generator regime toward being very large and expensive.
Because in Table 1 the hydrogen beam sail diameter is so large, we will focus the rest of this discussion on the mercury beam. Even so, the mercury beam Magsail has a 260 m diameter and 1 kg mass, if the superconducting hoop has a density of steel, the thickness must be no larger than 0.44 cm, if the density of carbon, 0.8 cm.
Magsail-Beam Interaction
Note that the sail diameter given in Table 1 is taken to be simply the diameter of the divergent beam encountering the Magsail. The diameter of the reflection region produced by the magnetic field of the sail could well be somewhat larger than the superconducting hoop diameter. (Of course, early in the acceleration, the beam will hit it at the axis where the magnetic field is greatest.)
When a Magsail driven by a neutral particle beam is at the early stages of the acceleration, the beam will have a considerably smaller spot size on the Magsail than it will later and will hit it at the axis where the magnetic field is greatest. Later on, as the Magsail flies away, the beam will reach a size dictated by its divergence. A question is: does the initial beam high intensity of the beam on the magnetic field tend to push the sails magnetosphere outward radially and make the effective diameter of the Magsail larger? If it does, then the beam divergence can be a bit larger and still strike the Magsail. Or, conversely one could accelerate the Magsail for a longer time because some of the beam would still be captured.
Simulations show the field being compressed; but they are of solar wind, which is taken to be uniform across a magnetic dipole. There are no simulations of the beam smaller than the sail. One would expect the loop generated field to be compressed in the direction of motion, but it seems reasonable for it to be inflated radially, especially if charged particles are trapped in it for significant periods of time.
Andrews and Zubrin have done single particle numerical calculations that do not include modeling dynamic effects (such as field distortions from magnetic pressure) and do not include any such “inflation” of the mirror due to trapped beam ions [7].
Figure 1 is taken from the late Jordan Kare’s NIAC report [8]. (From his figure, he considered using a nuclear detonation to accelerate a Magsail, which is not relevant to our discussion.) From the left a uniform solar wind strikes the Magsail, which in our case would be a non-uniform neutral particle beam. The beam encounters the peak of magnetic field along the axis of the sail. On the right of the figure, the field is distorted, producing a plasma interface shock against the magnetic field of the Magsail. Inflation of the magnetic field due to a particle beam pressure could occur. However, the effect would be to allow the beam divergence to be only a bit larger.
Note also that in this diagram the sail is shown as dragging the payload behind it as it accelerates. If part of the particle beam reaches the payload it could create substantial damage. Consequently, it might it be better to distribute the payload around the superconducting hoop where it would have the most protection against incoming charged particles. Note also the stability of the superconducting loop on a beam of finite width has not been investigated to date. However, the Starshot program is looking at this issue extensively.
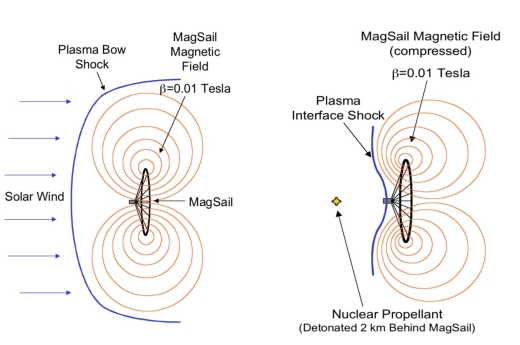
Figure 1: Interaction of streaming plasma flow with a Magsail. From Jordan Kare NIAC report [8].
The assumption that the moving magnetic field of the Magsail, seen in the frame of the beam as an electric field, ionizes the incoming neutral beam particles must be quantified.
Conclusions
Since beam divergence is fundamentally limited, high accelerations can be used to insure the sail will stay within the beam until it reaches the desired final velocity, even with microradian divergence. This leads to ultrahigh, 105 g’s, 106 m/s2 to accelerate to 0.06 c. The Starshot system, a laser beam-driven 1 gram sail with the goal of reaching 0.2c, has been quantified in a detailed system model by Kevin Parkin [9]. It too uses 105-106 g’s. Magsail-beam interaction remains an aspect of this concept that needs further study, probably by simulations. This promising method for interstellar travel should receive further attention.
References
1. G.A. Landis, “Optics and Materials Considerations for Laser-Propelled Lightsail,” IAA-89-664, 1989.
2. G. Nordley and A. J. Crowl, “Mass Beam Propulsion, An Overview”, JBIS 68, pp. 153-166, 2015.
3. Alan Mole, “One Kilogram Interstellar Colony Mission”, JBIS, 66, pp.381-387, 2013.
4. J, Benford, “Beam-Driven Sails and Divergence of Neutral Particle Beams” JBIS 70, pg. 449-452, 2017.
5. Report to the APS of the study on science and technology of directed energy weapons, Rev. Mod. Phys 59, number 3, part II, pg. 80,1987.
6. G. D. Nordley, “Relativistic Particle Beams for Interstellar Propulsion,” JBIS 46, pp 145-150,1993
7. Andrews, D. G. and R. M. Zubrin, “Magnetic Sails and Interstellar Travel”, JBIS 43, pp. 265-272, 1990
8. J. T. Kare, “High-acceleration Micro-scale Laser Sails for Interstellar Propulsion,” Final Report NIAC RG#07600-070, 2002.
www.niac.usra.edu/files/studies/final_report/597Kare.pdf. Accessed 03 Dec 2018.
9. K. L. G. Parkin, “The Breakthrough Starshot System Model”, Acta Astronautica 152, 370-384, 2018.



Having more than one beam has a large benefit by reducing the electrostatic divergence forces which are to the square. There is also larger molecules such as caged C60 carbon with silver or copper atoms inside, they are ionisable and very massive compared to mercury. Perhaps we could have atoms inside that can be spun up to act as gyroscopes to reduce divergence.
Forgot the article,
https://www.sciencedirect.com/science/article/abs/pii/S0022286015301551
I look forward to the engineering realities article.
Just considering 100k g’s. That is a lot. Any transient heterogeneity in the beam energy across the loop might more than just destabilize the craft, but tear it to pieces.
There seems to be a development scaling issue too. Can this be scaled down to run pilot tests, or does the experiment need to be done near the scale on the reference design?
Is there some reason why Hg was chosen as the heavy element. Is there any benefit in using another element like Xenon? What about molecules instead of atoms?
I agree about putting the payload at the loop. Not only does it give better protection from the beam, but also from any incoming material during the cruise phase to the target star. And a 1 kg payload seems more practical (today at least) to deliver a useful instrument package and return the data to Earth. I would like to see some suggestions for maneuvering in the target system to ensure close flybys and not hitting an obstacle in the system. It might be more than just unfriendly if it impacts an inhabited world.
What would be the appearance of the beam to an observer at the target solar system? How much of this might be detected beyond the target?
None, I would guess, because you don’t aim to where the target star is now, but to where it will be when the probe arrives.
Meaning that the beam will completely miss the star, because the particles are traveling much faster than the probe.
In the paragraph right above “Magsail-Beam Interaction”, where it says “if the superconducting hoop has a density of steel, the thickness must be no larger than 0.44 cm”, I believe that should be 0.44 mm, not cm; the same applies for the carbon case, of course.
cm looks right to me.
BoE calc. 260m diam ~=800 m circumference = 80,000 cm
density of steel = 8 gm/cm^3
Assume square x-section for simplicity:
so 80,000 . x^2/8 = 1000 gm
x^2 = 1/10. x = 1/3.16, i.e. about 1/3 cm.
So within the same range as 0.44 cm for a circular x-section.
Alex:
It’s not a big deal–it’s a wire, not a cable–but it really is mm.
Where you went wrong is in the line “so 80,000 . x^2/8 = 1000 gm”. It should be so 80,000 . x^2 = 1000 gm/8. That is to say volume =volume. The units on the left hand side of your equation are cm^6/g!
This is a very familiar problem to me. If I had a dime for every time I made an error like this I could fund Breakthrough Starshot!
Martin
You are right. My error.
I would hope you discuss this with Breakthrough Starshot.So much exciting news.
I went back to the 2014 article here on the subject and it discussed the possibility of using it for travel within the solar system. The article used an example of travel to Mars labeled Fast Interplanetary with a transit time of 8.7 days at 10 gees for a 3,000 KG mass. The article also mentions the requirement for a decelerator at the other end. How much more cost effective would such a system be for an architecture requiring a more modest acceleration at this end and utilizing the emerging technology of magnetoshell aerocapture for deceleration at Mars? This obviously falls within the walk before you run requirement of proving the technology before moving on to greater things.
A very exciting direction – 1000x the mass for only 3.5x the transit time!
Hold up on them thar lasers, Professor Lubin?
A one kilo payload sound much better than only a chip, the idea of sending a probe to another star start to make sense.
Magsails have advantages over the reflective kind.
The most obvious is that most part of it is not made from matter that can break.
The engineering challenge for the payload and to give it not only enough intelligence to do useful work at the target, but also redundancy for parts that might fail. The Voyagers and New Horizons have most likely taken several hits on their long journey.
But being hit by the same particle at 0,1 C could be very devastating.
One way to do this would to let the payload not be put in one box, but distributed to several locations, even single circuits placed separate with several connections so that one take over a task if another fail.
This idea have been suggested.
But that make any kind of shielding harder to make.
Perhaps it is better to put all electronics in a very narrow tube in the direction the spacecraft is flying.
Making the cross section as small as possible.
The redundant parts further down in to same tube. And mounting one very long ice plug in front.
An impact would blast the ice, and not anything important.
Why does the article speaks about maximizing the energy transfer? It clearly should had spoke about momentum instead.
A rule of thumb: do you want to kick the thing or cook it alive? If former is the case, it is momentum. It does not include the internal degrees of freedom, only the center-of-mass velocity.
I understand why energy transfer efficiency is important. How does this negate the issue of momentum transfer? Do we end up with some inefficient momentum transfer if we maximize energy transfer?
Because by optimizing the particles to effectively stop after hitting the magsail they lose the thrust the backscattering particles could had produced. They are wasting reaction mass here.
Paul Gilster, James Benford, Alan Mole, or any other reader in the know: A FEW QUESTIONS! ONE: If a civilization more advanced than ours uses this method to explore multiple star systems,could the one-time “nuclear propellant” mentioned in Figure One be substituted with a collection of low-mass 50% matter – 50% antimatter pellets for a series of detonations allowing the probe to travel from one star system to the next, and so on? TWO: Assuming deceleration to 0.0003 lightspeed at each targeted destination and the magsail turned off to give the probe to “recharge” from the star’s solar energy, during this “dormant phase”, would the magsail become a rather inefficient lightsail and impart a very small acceleration to the probe? THREE: Since this is a magsail, and not a lightsail, it would not need to be perfectly reflective, so would its albedo be in the range of ten times that of the average comet? That last question should pretty much give away my intent here: A new paper up on exoplanet.eu(“Dust bombardment can explain the extremely elongated shape of 1I/`Oumuamua and the lack of interstellar objects.” by Vavilov, D. and Medvedev, Y. has dealt a potentially(waiting for Bialy and Loeb to respond)FATAL blow to their gigayears old “sentry buoy” concept, potentially leaving ONLY the “more exotic” DELIBARATE probe as a viable non-natural explanation for `Oumuamua and all its peculiarities. Answers to these three questions would be appreciated. Thanks.
Extreemely high accelerations might be relevant for extreemely smal sailcraft , but if we want to go beyond that something else is needed . The only workable solution is to have several additional independant particle beam-sources positioned along the line of acceleration . Each one will push the sail only for a few seconds while the beam can be focused , and so the energy demands on each can be relatively limited .
This sceme open up several new problems , but all of them are at least theoreticly solvable , which is more than can be said for some other plans
If neutral beam divergence is inevitable, why not re-converge the beam? A high-energy Hydrogen beam is likely to be paramagnetic. This could give a handle on beam refocusing, perhaps via a magnetic field somewhere down the beamline. Has this possibility been evaluated?
R LeVitt,
The beam can’t be ‘reconverged’ very effectively, since the whole point of a neutral particle beam is to avoid it being dispersed by magnetic fields – that’s why it’s neutralised after the particles are initially accelerated electromagnetically. A laser ‘ring’ might allow some reconverging, but the power levels and efficiency requirements make it very difficult. Plus the beam could end up reionized, defeating the whole neutralisation process.
Wait a minute here: We have a neutral particle beam interacting with a dipole field generated by a current loop, where the axis of the loop is aligned with the beam? And we’re expecting the neutral particles to be ionized by the induced voltage?
Look, the induced voltage is the cross product of the field and the particle’s velocities, and if the particles are entering parallel to the axis of the coil, you’re minimizing the induced voltage. Along that axis the beam will go through as though the field weren’t there.
Maximum interaction with the field will be where you’re approaching it perpendicular to the field lines, the center of the coil is effectively a hole.
While I cannot get past the JBIS paywall, this reference to Andrews is most helpful and seems to answer many of the questions.
D.G. Andrews Interstellar propulsion opportunities using near-term
technologies Acta Astronautica 55 (2004) 443 – 451
There’s a fundamental difference between a magnetized plasma hitting a magnetic field, and a neutral particle beam. In the former case, the field carried along by the plasma has to displace the magnetic field in order for the plasma to enter that volume of space.
In the latter case, the neutral particles don’t “see” the magnetic field, (Barring some weak dipole effects.) until the induced voltage gets high enough to ionize them.
As I point out, the induced voltage is the cross product of the particle velocity and the field, and so goes to zero where the velocity is aligned with the field. Basically the only place the field will be effective at stopping a neutral particle beam is where the field lines are perpendicular to the beam.
Unless you can create a condition where the part of the beam that ionizes creates a dense enough plasma to ionize the rest of the beam by collision. That might work.
As soon as I saw the title, I was thinking of the Plasma Magnet…
https://centauri-dreams.org/2017/12/29/the-plasma-magnet-drive-a-simple-cheap-drive-for-the-solar-system-and-beyond/
…and I distinctly remember thinking at the time, if the velocity is limited by solar wind speed, why not use particle beams the same way lasers extend the performance of a solar sail? The authors briefly touch on inflation of the mirror by the incoming beam; I’d love to see if these concepts can synergistically resolve their respective drawbacks.
Driving magsails, plasma magnets, and electric sails with the solar wind assume the wind is ionized, not a neutral beam. The neutral beam is more like that of the exhaust of an ion engine where the ions are neutralized on emission.
Reading the Andrews paper, it seems the neutral beam may be a neutral plasma. This will be the same as a “concentrated solar wind”, albeit with different ions if Hg or some other atom or molecule is ionized. I await some clarification for this proposal.
Some questions; answers from Alan Mole:
Question
Alex Tolley January 3, 2019, 17:15
I look forward to the engineering realities article.
Just considering 100k g’s. That is a lot. Any transient heterogeneity in the beam energy across the loop might more than just destabilize the craft, but tear it to pieces.
Answer
— I believe it is fairly easy to get 50,000 g’s, and has been for some time. Proximity fuses in artillery shells came in at the end of WW2. And the shells dropped to ~1 g after leaving the barrel. 100,000 g’s is not much of a stretch.
https://en.wikipedia.org/wiki/G-force
Rating of electronics built into military artillery shells[33] 15,500 g
Analytical ultracentrifuge spinning at 60,000 rpm, at the bottom of the analysis cell (7.2 cm)[34] 300,000 g
Question
There seems to be a development scaling issue too. Can this be scaled down to run pilot tests, or does the experiment need to be done near the scale on the reference design?
Answer
I see no reason it could not be tested on a smaller scale, though final speed would not be as high because the sail would not be the same diameter. A long straight stretch of a mine or cavern would allow for measurement of force on the sail and propagation of the beam, though of course that would not allow the sail to accelerate.
Question
Michael Holt January 3, 2019, 20:25
What would be the appearance of the beam to an observer at the target solar system? How much of this might be detected beyond the target?
Answer
I doubt that it would be detectable because the solar wind would be much brighter. And you’d have to be looking at Sol during the 18 seconds the beam was running. Plus, all the ions are left at rest after reflection by the sail — or so we are supposing with 100% efficiency. Certainly most are left at rest or reflected at various angles and will never reach the target system.
Alan Mole
When looking around the website of John Hopkins university I got an answer myself to g-forces and electronics from the very same university that built the New Horizons.
Called proximity fuses – these can indeed withstand extremely high g-forces.
https://www.jhuapl.edu/About/DefiningInnovations
Old news we are now clearing over 200 000 g electronics.
Michael: thanks for the reference to the C60 carbon. I'll look into what it would give us. The fundamental divergence of neutral particle beam is caused by the problem of by the act of the neutralization itself. So the basic divergence is not due to electrostatics.
Martin & Alex: You’re right; it’s 0.44 mm.
Alex: I agree that one has to consider nonuniform forces on the hoop. Note that the power ramps up as the sail speed rises, so that the acceleration is gradual starting from small value. Using molecules would indeed be much heavier, but one has to make to ensure that you can actually have a source for the low-divergence molecular beam. I agree that a one kilogram payload is going to be a lot more feasible at the one grant to the gram scales the payloads of starship. Having some maneuverability at the target would require subsystems of a nontrivial mass. Note that because of the very short launch time, we could send a whole constellation of such probes and rely upon statistics to have some of them both survive and be proximate to interesting targets in the target system. Having a 1 kg object is to hit that inhabited world at even 0.06c is not going to be damaging. The amount of energy is high, ~100 TJ, but the impact on the exoplanet atmosphere will tear it apart in short order.
Michael Holt: First is the fact that the particles are reflected from the hoop and do not go on beyond. Second, with a launch driven by an intense beam to arrive years later at a neighboring stellar system, the sailship would be launched toward where the stellar system will be when the ship arrives. The ratio of the distance the star would move to the beam spot size is driven by the average velocity of the star relative to stars in our stellar neighborhood, typically 20 km/s. That ratio varies from 10^4 to 10^7. The angle of the radiated beam with respect to the light path between the two stars is larger than the width of the beam. Thus, the beam is generally not observable from the target planetary system.
David: Our next piece here, appearing in a few days, compares this neutral beam approach to Starshot.
Bill: This technology would certainly be developed for interplanetary transits in its early days. There’ll be earlier embodiments at lower speeds. Aerocapture at Mars would be for interplanetary–scale speeds such as 1 – 10 km/s.
ole burde: Certainly later embodiments could have a higher masses and multiple accelerators positioned along the line of acceleration. However, they would be deployed in space pretty far apart. For our worked example, the sailcraft will have traveled a hundred thousand miles when the acceleration is over.
R LeVitt: Converging the beam will actually increase the beam divergence. Divergence is more like temperature rather than a uniform direction for all the particles. And then when it exits the magnetic field there is a natural divergence produced by the diverging field itself.
There is also the possibility of using nanotube needles filled with high density materials. They can be given a low charge to mass ratio which would require a longer accelerator but the charge recombination disturbance would be smaller due to the mass.
https://www.advancedsciencenews.com/the-worlds-smallest-pipettes-capillary-action-in-carbon-nanotubes/
Regarding magnetoshell aerocapture, which I mentioned in my original post, and not simply aerocapture, the minimum speed mentioned for the technology to work is reported to be 8 kps for an earth type atmosphere. Discussions of using the tech range up to 40 kps, possibly more. Certainly enough to serve as a decelerator at a destination with an atmosphere.
@ James & Alan
Regarding the acceleration forces. The ability of electronics in compact artillery shells to withstand high g forces is not relevant here. Conceptionally, a thin (0.44 mm diameter) steel wire loop would fold up like a Dali clock if not fully supported.
Consider the problem if the loop drifts off center from the particle beam so that the g-forces just act on part of the hoop. The loop will start to rotate and may even fold up. I think I can show that it would break as well.
Let’s assume the loop drifts off beam and the g-forces are kept to just a part of the loop. I will assume that the loop is stabilized structurally by “spokes” to a point behind the loop (and probably in front too) like some sail designs. I will assume the guy wires are also steel of the same diameter. Each guy wire supports X meters of loop.
The tensile strength of steel is about 40,000 lbs/inch^2 (2790 kg/cm^2 if I have done the calcs correctly). The guy wire of 0.44 mm diameter can support 4.25kg (at 1 g)
Assume the guy wire supports 10 meters of loop. This portion masses 0.012 kg. Therefore the guy wire would break if a little over 350 g’s was applied to it, just a 0.35% differential in the 100k g’s.
It is not at simple as this, and certainly, the guy wire could be made of carbon fiber (or nanotube) to overcome this problem. The point is that 100k g’s is a lot to subject the structure to and that even small non-uniformity of the beam across the loop could potentially deform and even break it. However, I have no doubt that good design can overcome this issue, although it may be as difficult as that regarding the sail design for Breakthrough Starshot.
OT. This paper seems to include the same idea as Zubrin for his CD post on propulsion. The Dipole Drive: A New Concept for Space Propulsion
Beam Space Propulsion* by Bolonkin.
Concept in this Article is not on real word physic, but on wishful thinking. Charged particles in AB engine are deflected not in direction perpendicular ti magnetic field but along this field :-) etc. etc. etc.
One thing I agree – this idea is equal to Zubrin’s dipole drive, both far from physic laws.
@James Benford: “For our worked example, the sailcraft will have traveled a hundred thousand miles when the acceleration is over.”
This suggests a double-whammy approach, with a second beamer on the Moon. Alignment windows would be spaced one month apart, for certain target stars.
Alex Tolley: Indeed, artillery shells are made to understand incredible accelerations in the muzzle for a short time. I have worked a bit with such shells and I can assure you they are very carefully designed to allow no place for elements of the shell to move relative to one another in unused spaces!
You’re right, the differential accelerations, which are inevitable in realistic system, would tear it apart in short order. Even using the upper bounds of what carbon materials could do would give an order magnitude higher acceleration. So this configuration is impractical. Note that the aspect ratio of this hoop is approximately a million!
We chose Mercury as a heavier atom because Geoff Landis used it in his paper on this subject. Using heavy molecules is attractive, provided that one can be accelerated from a source.
Brett Bellmore: You’re right, the force from the ionizing electric field will be null on axis. It is maximized where the magnetic field is perpendicular to the velocity and therefore the force is an annulus around the axis of the sailcraft. Therefore one would want to use a hollow neutral particle beam so as not to waste the center of it. It is quite possible to generate such a hollow beam. It’s also attractive because the force is now applied out toward the where the hoop is, rather than on axis, where there no matter to accelerate.
Unfortunately, there IS matter on the axis, likely: The payload.
That would be my real concern: The coil is nicely shielded from that high energy particle beam by the magnetic field, but a payload hung from it on the center would not be. And you likely won’t be able to maintain a hollow beam for long, as the divergence approaches the beam radius.
Perhaps the payload could be distributed along the hoop?
I have an idea that may work with magsails, plasma-magnet-drives or the dipole drive that would use magnetic field reconnection to accelerate them. Now at first I was thinking using solar flares but having to wait around near the sun plus the high probability of frying the electronics does not sound good. But we have a very nearby source that may due the trick: Magnetic Reconnection in the
Earth’s Magnetotail. Take a look at these articles and see if this might work:
Magnetic Reconnection in the Earth’s Magnetotail.
http://www.publish.csiro.au/ph/pdf/PH850981
EARTH’S DYNAMIC MAGNETIC SHIELD.
https://www.nap.edu/read/11188/chapter/5
Just an idea, might be a lot of energy shooting away from earth and with the ability of a magnetic field to surf on it, all you need is the control of the direction…
Another idea, 2010: The Year We Made Contact, the best part was the spacecraft kevlar balloons using the atmosphere of Jupiter to slow down. So would this also work with magnetic sails?
There is work to demonstrate the viability of magnetic fields for aerobraking. The benefits are much lower mass than physical aeroshells. paper.
The Leonov’s ballutes in 2010 looked cool, but I don’t know whether they would have worked as envisaged in the movie version. [Amazing to think the much touted CG of the aerobraking was state of the art when the movie was made. Now they look very primitive. And those outdated hopelessly laptops and computers… ]
Here is something a little more up to date that is showing super-Alfvenic electron jets reaching 20,000 km/s or o.o66c during magnetic reconnection.
Satellites reveal the microphysics of magnetic reconnection.
Laminar electron dynamics drive reconnection on the side of Earth away from the Sun.
https://physicstoday.scitation.org/do/10.1063/PT.6.1.20190107a/full/
Physics > Space Physics
Electron-Scale Dynamics of the Diffusion Region during Symmetric Magnetic Reconnection in Space.
“Magnetic reconnection is an energy conversion process important in many astrophysical contexts including the Earth’s magnetosphere, where the process can be investigated in-situ. Here we present the first encounter of a reconnection site by NASA’s Magnetospheric Multiscale (MMS) spacecraft in the magnetotail, where reconnection involves symmetric inflow conditions. The unprecedented electron-scale plasma measurements revealed (1) super-Alfvenic electron jets reaching 20,000 km/s, (2) electron meandering motion and acceleration by the electric field, producing multiple crescent-shaped structures, (3) spatial dimensions of the electron diffusion region implying a reconnection rate of 0.1-0.2. The well-structured multiple layers of electron populations indicate that, despite the presence of turbulence near the reconnection site, the key electron dynamics appears to be largely laminar.”
https://arxiv.org/abs/1809.06932v1
Well, it looks like an electron jet is already up in space nearby the earth and it doesn’t cost much to get a ride so what drives would work in this type of environment – magsails, plasma-magnet-drives or the dipole drives?
What about Jupiter’s magnetic reconnection, it is the giant in the solar system, so could it’s magnetic reconnection be that much more powerful? Further away, but the dynamics may be different and speeds higher and maybe high speed ion jets?
Just want to say I really like the James Benford reports and his responses.Thanks Paul.
My pleasure, David. And I really appreciate the chance to print this work, which moves the ball forward. Many thanks to Jim and Alan.
I am not sure how well the magnetic field will handle the huge forces put on it, it may collapse completely.
Perhaps the optimum mission will be some combination of Project Starshot, Project Dragonfly, neutral beaming and a way to magsail brake at the destination, as exemplified here
https://arxiv.org/abs/1701.08803
https://arxiv.org/abs/1704.03871
Alex has described the problem of differential forces on the sail structure.
This is a control problem. Assume 100 beam generators arranged in a circle, on Earth, each generating a beam of 1,000,000 N/100 = 10,000 N (= 2200 pounds). Each is on a foundation and has force measuring equipment.
The sail is 260 m diameter, 820 m circumference, 8 m between beams. One beam starts generating 1/100,000 extra force, creating a ripple in the sail. That segment accelerates at 1g relative to the rest, 10 m/s^2. Supposing this goes on for one hundredth of a second, then that segment reaches a speed of .1 m/s relative to the rest of the loop. In a maximum of 18 seconds during sail acceleration it reaches a maximum magnitude of 1.8 m – a reasonable amount. But it is probably corrected.
If the measurement system and control computer catch this and correct with about -2 g’s, then the segment slows and reverses direction, flattening it at some optimal time. (Think of 100 masses each driven by a beam, and one gets out ahead of the rest. It is slowed, but should it reach the rest at ~.03 seconds, 18 seconds or what?)
This is a nice dynamics problem, but it basically requires measuring the force between beam generator and its foundation to one part in 100,000 every hundredth of a second, and controlling to correct any variation. For computers that now do exaflops (10^18 per second,), this is trivial.
Variations of the magnetic field of the sail and pointing accuracy may be problems. It should be possible to measure variation in the magnetic field during development using low accelerations.
Alan
Alan: I don’t think that’s going to work because the transit time between sail and the ground-based beam generators is much longer than the time over which perturbations to the sail will develop. Sail perturbations propagate at an acoustic velocity in the hoop material. For example, the velocity of sound in a thin steel rod is 5 km/s, the perimeter of the sail is 0.8 km. Therefore 1/12 second is the time for the perturbation, going in both directions, to travel half the way around the sail. By the time acceleration stops, when the forces are the largest, the transit time back to the ground is 2 seconds. Therefore the sail could be torn apart by perturbations before the ground even hears of it.
“zero velocity” – Absolte? Relative?
Does all particle from this beam after magsail impact forms gas cloud moving together with starship composing single “body”?
If “none of the energy is left in the beam” – should we conclude that authors invented ideal fridge that is able to cool metter down to absolute zero? Which physical process allows so? Do we have example of similar effective cooler constructions in real life?
Jim Benford:
The waves go through the sail like the waves through a bullwhip, perpendicular to the wire not parallel to it, relatively slowly, on the order of seconds, like ocean waves. If those can be measured there is time to correct them by varying the power of the beams.
But I was imagining we measured the force between the beam generators and their foundations and made immediate corrections to any variations.
Alan
I wonder if James Benford’s estimation of the transverse momentum imparted by stripping electrons from H- is a bit pessimistic. He asserts that the stripped electron will have kinetic energy equal to the affinity energy of hydrogen (0.7 eV). But shouldn’t the stripped electron actually have kinetic energy of order the photon energy *minus* the affinity energy? IE if the photoionizing light source is precisely controlled, you could dramatically reduce the added dispersion. I think the limit would just be the momentum carried by the photon itself, p=h/lambda=3.7e-29 kg m/s for 0.7 eV photons. If that momentum is delivered 100% to hydrogen ion (proton) (which I believe is true to good approximation in photoionization), that gives a transverse velocity of 2.2e-2 m/s or an additional dispersion of 7.5e-10 radians for a beam propagating at 0.1c.