What can we say about the possible appearance and spread of civilizations in the Milky Way? There are many ways of approaching the question, but in today’s essay, Dave Moore focuses on a recent paper from Robin Hanson and colleagues, one that has broad implications for SETI. A regular contributor to Centauri Dreams, Dave was born and raised in New Zealand, spent time in Australia, and now runs a small business in Klamath Falls, Oregon. He adds: “As a child, I was fascinated by the exploration of space and science fiction. Arthur C. Clarke, who embodied both, was one of my childhood heroes. But growing up in New Zealand in the ‘60s, such things had little relevance to life, although they did lead me to get a degree in biology and chemistry.” Discovering like-minded people in California, he expanded his interest in SETI and began attending conferences on the subject. In 2011, he published a paper in JBIS, which you can read about in Lost in Time and Lost in Space.
by Dave Moore
I consider the paper “If Loud Aliens Explain Human Earliness, Quiet Aliens Are Also Rare,” by Robin Hanson, Daniel Martin, Calvin McCarter, and Jonathan Paulson, a significant advance in addressing the Fermi Paradox. To explain exactly why, I need to go into its background.
Introduction and History
In our discussions and theories about SETI, the Fermi paradox hangs over them all like a sword of Damocles, ready to fall and cut our assumptions to pieces with the simple question, where are the aliens? There is no reason not to suppose that Earth-like planets could not have formed billions of years before Earth did and that exosolar technological civilizations (ETCs) could not have arisen billions of years ago and spread throughout the galaxy. So why then don’t we see them? And why haven’t they visited us, given the vast expanse of time that has gone by?
Numerous papers and suggestions have tried to address this conundrum, usually ascribing it to some form of alien behavior, or that the principle of mediocrity doesn’t apply, and intelligent life is a very rare fluke.
The weakness of the behavioral arguments is they assume universal alien behaviors, but given the immense differences we expect from aliens—they will be at least as diverse as life on Earth—why would they all have the same motivation? It only takes one ETC with the urge to expand, and diffusion scenarios show that it’s quite plausible for an expansive ETC to spread across the galaxy in a fraction (tens of millions of years) of the time in which planets could have given rise to ETCs (billions of years).
And there is not much evidence that the principle of mediocrity doesn’t apply. Our knowledge of exosolar planets shows that while Earth as a type of planet may be uncommon, it doesn’t look vanishingly rare, and we cannot exclude from the evidence we have that other types of planets cannot give rise to intelligent life.
Also, modest growth rates can produce Kardeshev III levels of energy consumption in the order of tens of thousands of years, which in cosmological terms is a blink of the eye.
In 2010, I wrote a paper for JBIS modeling the temporal dispersion of ETCs. By combining this with other information, in particular diffusion models looking at the spread of civilizations across the galaxy, it was apparent that it was just not possible for spreading ETCs to occur with any frequency at all if they lasted longer than about 20,000 years. Longer than that and at some time in Earth’s history, they would have visited/colonized us by now. So, it looks like we are the first technological civilization in our galaxy. This may be disappointing for SETI, but there are other galaxies out there—at least as many as there are stars in our galaxy.
My paper was a very basic attempt to deduce the distribution of ETCs from the fact we haven’t observed any yet. Robin Hanson et al’s paper, however, is a major advance in this area as it builds a universe-wide quantitative framework to frame this lack of observational evidence and produces some significant conclusions.
It starts with the work done by S. Jay Olsen. In 2015, Olson began to bring out a series of papers assuming the expansion of ETCs and modeling their distributions. He reduced all the parameters of ETC distribution down to two: (?), the rate at which civilizations appeared over time, and (v) their expansion rate, which was assumed to be similar for all civilizations as ultimately all rocketry is governed by the same laws of physics. Olsen varied these two parameters and calculated the results for the following: the ETC-saturated fraction of the universe, the expected number and angular size of their visible domains, the probability that at least one domain is visible, and finally the total expected fraction of the sky eclipsed by expanding ETCs.
In 2018, Hanson et al took Olsen’s approach but incorporated the idea of bringing in the Hard Steps Power Law into modeling the appearance rate of ETCs, which they felt was more accurate and predictive than the rate-over-time models Olsen used.
The Hard Steps Power Law
The Hard Steps power law was first introduced in 1953 to model the appearance of cancer cells. To become cancerous an individual cell must undergo a number of specific mutations (hard steps i.e. improbable steps) in a certain order. The average time for each mutation is longer than a human lifetime, but we have a lot of cells in our body, so 40% of us develop cancer, the result of a series of improbabilities in a given cell.
If you think of all the planets in a galaxy that life can evolve on as cells and the ones that an ETC arises on being cancerous, you get the idea. The Hard Steps model is a power law, so the chances of an outcome happening in a given period of time is the inverse of the chance of a step happening (its hardness) to the power of the number of steps. Therefor the chance of anything happening in a given time goes down very rapidly with the number of hard steps required.
In Earth’s case, the given period of time is about 5.5 billion years, the time from Earth’s origin until the time that a runaway greenhouse sets in about a billion years from now.
The Number of Hard Steps in our Evolution
In 1983 Brandon Carter was looking into how likely it was for intelligent life to arise on Earth, and he thought that due to the limitations on the time available this could be modeled as a hard step problem. To quote:
This means that some of the essential steps (such as the development of eukaryotes) in the evolution process leading to the ultimate emergence of intelligent life would have been hard, in the sense of being against the odds in the available time, so that they are unlikely to have been achieved in most of the earth-like planets that may one day be discovered in nearby extra-solar systems.
Carter estimated that the number of hard steps it took to reach our technological civilization was six: biogenesis, the evolution of bacteria, eukaryotes, combogenisis [sex], metazoans, and intelligence. This, he concluded, seemed the best fit for the amount of time that had taken for us to evolve. There has been much discussion and examination of the number of hard steps in the literature, but the idea has held up fairly well so Hanson et al varied the number of hard steps around six as one of their model variables.
The Paper
The Hanson paper starts out by dividing ETCs into two categories: loud aliens and quiet aliens. To quote:
Loud (or “expansive”) aliens expand fast, last long, and make visible changes to their volumes. Quiet aliens fail to meet at least one of these criteria. As quiet aliens are harder to see, we are forced to accept uncertain estimates of their density, via methods like the Drake equation. Loud aliens, by contrast, are far more noticeable if they exist at any substantial density.
The paper then puts aside the quiet aliens as they are, with our current technology, difficult to find and focuses on the loud ones and, in a manner similar to Olsen, runs models but with the following three variables:
i) The number of hard steps required for an ETC to arise.
ii) The conversion rate of a quiet ETC into a loud, i.e. visible, one.
iii) The expansion speed of a civilization.
In their models, (like the one illustrated below) a civilization arises. At some point, it converts into an expansive civilization and spreads out until it abuts a neighbor at which point it stops. Further civilizations in the volume that is controlled are prevented from happening. Results showing alien civilizations that are visible from our point of view are discarded, narrowing the range of these variables. (Note: time runs forward going down the page.)
Results
In a typical run with parameters resulting in them not being visible to us, expansive civilizations now control 40-50% of the universe, and they will finish up controlling something like a million galaxies when we meet one of them in 200 million year’s time. (Note, this paradoxical result is due to the speed of light. They control 40-50% of the universe now, but the electromagnetic radiation from their distant galaxies has yet to reach us.)
From these models, three main outcomes become apparent:
Our Early Appearance
The Hard Step model itself contains two main parameters, number of steps and the time in which they must be concluded in. By varying these parameters, Hanson et al showed that, unless one assumes fewer than two hard steps (life and technological civilizations evolve easily) and a very restrictive limit on planet habitability lifetimes, then the only way to account for a lack of visible civilizations is to assume we have appeared very early in the history of civilizations arising in the universe. (In keeping with the metaphor, we’re a childhood cancer.)
All scenarios that show a higher number of hard steps than this greatly favor a later arrival time of ETCs, so an intelligent life form producing a technological civilization is at this stage of the universe is a low probability event.
Chances of other civilizations in our galaxy
Another result coming from their models is that the higher the chance of an expansive civilization evolving from a quiet civilization, the less the chance there is of there being any ETCs aside from us in our galaxy. To summarize their findings: assuming a generous million year average duration for a quiet civilization to become expansive, very low transition chances (p) are needed to estimate that even one other civilization was ever active anywhere along our past light cone (p < 10?3), or existed in our galaxy (p < 10?4), or is now active in our galaxy (p < 10?7).
For SETI to be successful, there needs to be a loud ETC close by, and for one to be close by, the conversion rate of quiet civilizations to expansive, loud ones must be in the order of one per billion. This is not a good result pointing to SETI searches being productive.
Speed of expansion
The other variable used in the models is the speed of expansion. Under most assumptions, expansive civilizations cover significant portions of the sky. However, when taking into account the speed of light, the further distant these civilizations are, the earlier they must form for us to see them. One of the results of this relativistic model is that the slower civilizations expand on average, the more likely we are to see them.
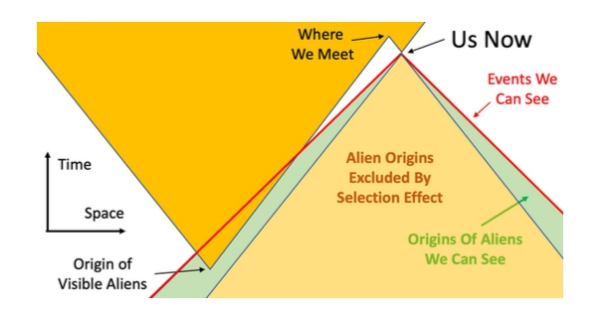
This can be demonstrated with the above diagram. The orange portion of the diagram shows the origin and expansion of an ETC at a significant proportion of the speed of light. We—by looking out into space are also looking back in time—can only see what is in our light cone (that which is below the red line), so we see the origin of our aliens (say one billion years ago) and their initial spread up to about half that age. After which, the emissions from their spreading civilization have not yet had time to reach us.
The tan triangle represents the area in space from which an ETC spreading at the same rate as the orange aliens would already have arrived at our planet (in which case we would either not exist or we would know about it), so we can assume that there were no expansive aliens having originated in this portion of time and space.
If we make the spread rate a smaller proportion of the speed of light, then this has the effect of making both the orange and tan triangles narrower along the space axis. The size of the tan exclusion area becomes smaller, and the green area, which is the area that can contain observable alien civilizations that haven’t reached us yet, becomes bigger.
You’ll also notice that the narrower orange triangle of the expansive ETC crosses out of out of our light cone at an earlier age, so we’d only see evidence of their civilization from an earlier time.
The authors note that the models rely on us being able to detect the boundaries between expansive civilizations and unoccupied space. If the civilizations are out there, but are invisible to our current instruments, then a much broader variety of distributions is possible.
Conclusions
We have always examined the evolution of life of Earth for clues as to the distribution alien life. What is important about this paper is that it connects the two in a quantitative way.
There are a lot of assumptions build into this paper (some of which I find questionable); however, it does give us a framework to examine them and test them, so it’s a good basis for further work.
To quote Hanson et al:
New scenarios can be invented and the observable consequences calculated immediately. We also introduce correlations between these quantities that are obtained by eliminating dependence on ? [appearance rate], e.g. we can express the probability of seeing at least one domain as a function of v [expansion velocity] and the currently life-saturated fraction of the universe based on the fact we haven’t see or have encountered any.
I would point out a conclusion the authors didn’t note. If we have arisen at an improbably early time, then there should be lots of places (planets, moons) with life at some step in their evolution, so while SETI searches don’t look promising from the conclusions of this paper, the search for signs of exosolar life may be productive.
This paper has given us a new framework for SETI. Its parameters are somewhat tangential to the Drake Equation’s, and its approach is to basically work the equation backwards: if N=0 (number of civilizations we can communicate with in the Drake equation, number of civilizations we can observe in this paper), then what is the range in values for fi (fraction of planets where life develops intelligence), fc (fraction of civilizations that can communicate/are potentially observable) and (L) length of time they survive. The big difference is that this paper factors in the temporal distribution of civilizations arising, which is not something the Drake Equation addressed. The Drake equation, for something that was jotted down before a meeting 61 years ago, has had a remarkably good run, but we may be seeing a time where it gets supplanted.
References
Robin Hanson, Daniel Martin, Calvin McCarter, Jonathan Paulson, “If Loud Aliens Explain Human Earliness, Quiet Aliens Are Also Rare,” The Astrophysical Journal, 922, (2) (2021)
Thomas W. Hair, “Temporal dispersion of the emergence of intelligence: an inter-arrival time analysis,” International Journal of Astrobiology 10 (2): 131–135 (2011)
David Moore, “Lost in Time and Lost in Space: The Consequences of Temporal Dispersion for Exosolar Technological Civilizations,” Journal of the British Interplanetary Society, 63 (8): 294-302 (2010)
Brandon Carter, “Five- or Six-Step Scenario for Evolution?” International Journal of Astrobiology, 7 (2) (2008)
S.J. Olson, “Expanding cosmological civilizations on the back of an envelope,” arXiv preprint arXiv:1805.06329 (2018)



In the preamble you sate;
With our sample of one, we are applying high Bayesian prior to that assumption without any data to support it. It may be true, or it may not.
Then this:
As the KIII level requires capturing the energy of a galaxy of stars, the expansion time to reach all the stars implies that this cannot be reached in a time less than the expansion time, i.e. 10s of millions of years. AFAICS, the only way around this spatial limitation is to create supernovae to generate the energy to be captured. The civilization can reach KIII levels of energy use by accelerating the energy emission of local stars.
I do hope this proves true:
However, that is my bias in hoping the mediocrity principle holds true, even as we have no evidence for it. Maybe that will be proven in a decade or two. But if it isn’t…
Lastly, the inherent assumption of these sorts of ETC papers is that despite paying lip service to “aliens will be different, as will their behaviors”, their detectable behavior has to be very human-like: technologically expansive in a physical way, almost Victorian in sensibility, much as Well’s Martians were effectively colonialists like the European empires. We seem to be trapped in this way of thinking, with the only argument being that some ETCs will act as we do, even if most do not. But consider if all emergent ETCs become transcendent, an evolution path of aliens (and Bowman, HAL9000) common in Clarke’s stories, then we might not detect them at all as we look for physical evidence. We may just detect life, but not ETCs, unless they go through the expansive phase before transcendence, leaving megastructures as archaeological artifacts.
Alex, some good points. This is a field where we have to make a lot of assumptions based on very thin evidence. And I would argue from the evidence we have so far that the principle of mediocrity does apply. The types of stellar systems are much more diverse than we imagined. Our observations are yet sensitive enough get a good size distribution and the Earth isolation zone around stars, but there is so far nothing to indicate Earth is a complete outlier. In fact, I can’t think of no evidence that the principle of meritocracy does not apply. Ward postulated that Earth’s moon was an outlier, but planetary formation modeling happily shows major planetary collisions, and we have another example of an Earth-moon like system Pluto and Charon. This does not mean that contradictory evidence will not turn up, but for the moment, I think best practices require us to assume it.
RE: The KIII level. I agree with you there. I put the line in to indicate that economic/energy consumption growth was not a limiting factor.
I’m going to address the alien universalist behavior argument in a stand alone post because other posters have bought this up.
To reach K3 within 10,000 years, a people need the equivalent of galaxy’s worth of star light within 10,000 years travel time. Conceptualizations live or die according to their fidelity and resolution to known physics. Convince us there is that much energy available within, let’s be generous, 10,000 light years of any system. Extending economic trends indefinitely without addressing where the energy is coming from is an 8-bit fantasy of a concept.
Let’s say very optimistically you could colonize at a rate of 0.1c in every direction. That would give you 1000 cubic lightyears worth of stars to work with.
Oversimplified that would mean you would somehow have to be able to increase the output of each star by a factor of 1 million. At least.
Gives a whole new meaning to the word “loud”
Hanson is not making an assumption about how typical aliens are likely to behave. He simply observes that being grabby is one such way for some aliens to be, and he limits his analysis to only those, since it is their destiny to dominate the universe. Nothing in physics prevents grabbiness; it only imposes a speed limit. You seem to think that Hanson speculated that aliens wouldn’t become blue hippies and live in a tree, based on shaky extrapolations from one case. He did no such thing. He is simply observing that blue hippie aliens will play no interesting role in the future of our universe. In the cool graphic he made, they are invisible.
If you believe that all kinds of hippie aliens exist, with all kinds of self-limiting institutions, you do not disagree with his analysis. You’re just thinking about civilizations that are soon to be ground up in the expansion wave of the grabby, which is why Hanson focuses on the latter. If you want to speak on topic, argue with him about the spacetime frequency of initiations of grabby expansion waves. Do you dispute that the graphic basically correctly describes the macro history and fate of the universe? Because if you don’t, you basically concede his point that we’re early, because we lack obvious and grabby aliens in our past lightcone. I can’t think of any reason to dispute the basic accuracy of the graphic. Time is long, the universe is big, and grabby civilizations are eminently possible.
I didn’t realize I gave you that impression. Rather, I was suggesting that “grabby aliens” may be an anachronistic, human behavior assumption. Other organisms do not expand as modern humans do, despite the superficial similarity to the spatial expansion of organisms. Look at this in another way, are there “grabby octopi”, or “grabby corvids”? In the terms of the Hanson paper, the emergence probability might collapse to an infinitesimally small value, with all that implies in the prevalence of ETC expansions. It does change the model, just the values for the last step phase.
From the paper:
This seems rather worrying to me. Very much in the alien invasion trope.
This is an interesting point, a possible counterfactual to the model. Suppose we accept that models of panspermia often show the probability of panspermia as being extremely low. One mechanism is Thomas Gold’s suggestion that it is due to biological astronauts leaving their “garbage” behind. [If only he had known at the time that the Apollo astronauts left bags of their “garbage” behind on the Moon!] If so, then after the first, improbable, emergence of a grabby civilization (GC) then the time taken for their garbage to evolve into another GC is so long, billions of years, that they are the only other GC. It may well be that we are going to be the first such GC.
10 million years is a long time, longer than most species survive. Given the rapid, cultural changes humans undergo, it seems unlikely that humans will be around in 10 million years. From this I would suggest that we don’t have anywhere near that length of time to become GCs, or indeed any technological civilization. Assume that our artificial evolution through gene engineering, and cultural evolution, that we speciate every 10 millennia, radiating out into new forms, more or less humanoid, but not necessarily so. Does that increase the speed at which any one of these new human species we becomes a GC, or does it mean that many, many post human species will evolve, perhaps restarting from scratch each time, never able to gain the time needed to become GCs. Given we are already starting to send out robot probes into interstellar space, I continue to support the idea that GCs will exist, but they will be machines not biological, and we will be their ancestors, at least in this galaxy. Furthermore, as machines cannot evolve without the prior emergence of intelligent biologicals, that any robotic GC will likely be a one-off event (ours), unless abiogenesis is common, as is the emergence of technological intelligence.
Thanks for the kind review. A few corrections:
“In 2018, Hanson” Actually we started at the end of 2020.
“To become cancerous … mutations in a certain order. ” Actually for cancer the order doesn’t matter.
“assuming a generous million year average duration for a quiet civilization to become expansive” Actually that’s assuming a million years duration til it dies, not til it becomes expansive.
What a pleasure to see you here, Dr. Hanson. Thanks so much for joining the discussion.
There’s plenty of circumstantial evidence that microbial life is common throughout the cosmos. It may not be conclusive, we only have one example, but it still seems likely. But we have absolutely no guarantees that multicellular life is common. Neither do we have any a priori reason to believe multicellular life, comparable in complexity to terrestrial vertebrates, are common. And if they are, we have absolutely no reason to believe “intelligence” (whatever THAT is) is an inevitable development of complex life forms. And we certainly don’t know if intelligent beings will necessarily develop technologically, so they can exert their influence across interstellar distances. Not only can we not state confidently that evolution must eventually lead to physics (radios and spaceships), neither can we conclude that exoplanets will provide the necessary resources. Can a submarine civilization develop fire, or electromagnetism, or metallurgy? Will a permanently opaque atmosphere allow the development of astronomy? What if there is no way to make clear glass on Planet X (no microscopes, no telescopes, no test tubes, no portholes or spacesuit visors).
We talk about “The Fermi Paradox” as if we really had a decent grasp of the spatial and temporal separations involved between even the most neighboring pair of civilizations. And all our speculations seem to be saturated with the suspicion that they will be just like us, aggressive, curious, gregarious toolmakers. They will either transmit a signal, or conduct planetary engineering works we can detect from light years away. Or they will actually travel here in little bubbles of artificial environment.
We got to where we are only after a long, long time; And then we developed at lighting speed (in geological/biological timescales). This does not prove, but it certainly suggests, our own evolution as an intelligent species with galactic ambitions is not a foregone conclusion. It sounds like an accidental and unexpected event, not an inevitable evolutionary development. We have no way of knowing they evolved the way we did. We have no way of knowing if anyone has evolved the way we did. We may not be unique, but com lasers may very well be.
All of our speculations on SETI, both optimistic and pessimistic, seem to assume they will be practically identical to us. And that is precisely what we should expect will not be the case. And whatever they are like, even if they are very similar to us, they will have gotten that way in a place very far away; either a long time ago, or a long time from now.
No, I’m not saying we should give up. But we should constantly remind ourselves of these obstacles so we don’t waste our time and effort looking in all the wrong places. And lets forget all about this “Fermi Paradox” nonsense. We haven’t been looking, or listening, anywhere near long enough.
Isn’t this an argument for Hanson’s step power-law model, albeit with life at the bacterial stage having a high probability? It then becomes an argument over the probabilities not being based on our sample of one. Our technology explosion has been just a recent phenomenon (science as a process + the industrial revolution) and was not universal across all cultures, just the European experience. Would any of the indigenous civilizations have eventually developed such a culture? China certainly failed to do so despite being one of the oldest continuous civilizations. If we look at a range of ancient civilizations, what was the rate of technological change over their period? European civilization[s] remained relatively static technologically until the industrial revolution when new technology just exploded. In just 300 years we have gone from crafts (even if impressive in some cases) to knowledge and an industrial base that has the stars in our sights. Are we just lucky in that regard, or unlucky in the event we terminate our civilization through our own means?
I don’t agree with the title of this paper. I makes an assumption that we are the loud aliens and we are first. We are quiet aliens to all other ET civilizations in our galaxy. A radio signal with a million watts of power will just barely reach our nearest star, Alpha Centauri at 4.3 lightyears away. None of our TV and radio broadcasts will make it there because they are no where near the required power and they will attenuate due to the inverse square law of EMR where the strength of the signal attenuates inversely proportional to the square of the distance from a source.
We could easily come up with a different idea which equally matches observations: Quiet Aliens are the norm or common and loud ones are rare considering UAP’s or UFO’s. We are the new kids on the block and the advanced ET’s with interstellar travel are part of a galactic club that has been around long before us which we can’t access because our technology is too primitive. When we get FTL technology, which is outside the light cone by the way which is why we can’t see their spacecraft moving at FTL, so we assume they are not there or don’t exist. A got the new kids on the block from Dr. Lawrence Krauss’s book the Physics of Star trek, the second edition which I read in 2007. I think I recall his idea was that most of the G class stars in our galaxy now are further in their main sequence hydrogen burning or are older than ours, so the life could have evolved on a planet 5 billion years before the birth of our solar system. When our solar system was born 4.5 billion years ago, that civilization would be 500 million years more advanced and today 5 billion years more advanced than us! I wonder what kind of technology a they would have. The level of advancement of technology is not considered in the Fermi Paradox, so we can assume we make the mistake of looking at life in our galaxy limited only to today’s standards of technology, and our present level of consciousness. It can be argued that K standards to judge technological advancement is too arbitrary or broad, so no useful information can be obtained.
The idea that we need to colonize our galaxy may be obsolete since it is based on the past exploration of our Earth first by the boat. It does not apply to space due to the vast distances. Once a ET civilization gets FTL interstellar travel, colonization becomes completely obsolete. Also what are the ethics of colonizing another world which already has life? It is ethical do to that? Planets without life can always be considered for colonization. What happens to an ET civilization which has been around for five billion years which is well beyond the main sequence burning for their planet staying in the life belt? Does it have the technology to live permanently in space, or do they go to another world and terraform it to keep their ethics intact, or do they share planets with other very technologically advanced civilizations?
” Once a ET civilization gets FTL interstellar travel, colonization becomes completely obsolete. ”
My favourite idea is that once you have the ability to carry out interstellar travel to colonize other worlds, you no longer have to. You either have technology allowing your species to prosper in variety of alien environments or to create sustainable artificial habitable environments. So the very technology that allows you to travel across the stars to colonize other planets would mean that colonization is no longer needed.
@Geoffrey, @Wojciech
I don’t see the logic in this. There are many reasons for a group to want to put distance between themselves and the main population of their species.
If by colonization, you mean living on a planetary surface, then yes, that may be true, although there wil likely be those that want to live on a planetary surface, even if it is inhospitable outside their domes. But building new habitats around another star, whether that system is inhabited or not, is still colonization.
I think it also depends on th emeans to travel. STL might imply worldships, or it might imply seedships. FTL might imply worldships, or small spacecraft. On Earth, one might be convinced that living on an ocean liner is feasible, but I don’t think many people would want to live inside an aircraft, or submarine Fast travel in small ships might increase the desire to colonize other stars, possibly in cities and arcologies on or below a planetary surface.
As for the idea of filling the system with habitats that could support trillions of individuals, thet may be desirable for some, but anathema to others, just as some people like to live in cities, while others prefer a more isolated place to live.
I think we can expect all sorts of behaviors and responses, both within and between alien species.
IIRC it was Robert Freitas who suggested that the decline in dinosaur diversity in the late Cretaceous might have resulted from the arrival of alien settlers on Earth, and that the asteroid that destroyed the dinosaurs was sent by rival aliens to destroy the settlers. His more serious point was that the Earth may well have been visited by aliens but any trace of them is undiscovered or obliterated. He also points out that there could be aliens around nearby stars or even in our solar system, but unless they make themselves glaringly obvious we probably couldn’t detect them. So any assumptions we make based on lack of detection are on very shaky ground.
Hi NS
I always wondered where Ken Mcleod got the idea of the Monkey-Spiders being taken out by the Chixulub impactor from (in his “Engines of Light” trilogy). Do you remember the Freitas paper’s title? Or was it in “Xenology”?
This appears to be an instance of “IRI” (I Recalled Incorrectly).
I can find no reference in anything online by Robert Freitas about the dinosaur extinction asteroid and aliens, although I recalled reading it and attributed it to him. I did however find this by David Brin, indeed in “Xenology”:
https://www.davidbrin.com/nonfiction/xenology2.html
Obviously I should have double-checked before posting!
Hmm, David Brin’s “Xenology” is different from the Robert Freitas one (possibly the source of my confusion?). In any case, the dinosaur asteroid reference is Brin’s.
Another possibility (and this may greatly reduce the chances of finding an ETC in any time cone) is that once technology of a certain level is achieved (possibly nuclear fission or just advanced weapons of other kinds or induced climate change), then that civilization has a very short future, possibly hundreds of years or less. Therefore no expansion to a large volume of space occurs. The author mentions a time frame of 20,000 years or more. This may not be compatible with the results of technological development and progression (wars, plagues either engineered or not, environmental destruction and so on).
Well, SETI needs to get its ass off the fence because as we saw this May 17th the ETs have been making it very obvious. 80 some years of obvious interaction on the most personal level long before SETI was around! This game of ignoring UAPs is arrogant to the extreme and makes us the dumbest civilization in the galaxy. Why do you think Fermi made such a remark, because the average person on this planet lived in a rural environment and had little understanding of the possibility of wormholes or interstellar travel in 1950s and the world had a much more important problem, the chance of destroying ourselves with nuclear weapons.
It seems we have advanced tremendously in those 70 years since that statement but we still have the same mentality, “Ignorance”.
It’s hard to understand the persistence of such an inane tautology as Fermi’s Paradox.
Imagine someone looking up from their desk for a split second, failing to see another person in that time and visual span, and therefore deciding that one of the following seems likely: (1) No other people exist; (2) if other people exist, they must be “hiding” from this person; (3) other people in this office are ineffably bizarre, and must exist on a level beyond immediate sensation.
SETI is a fine effort with laudable goals, but the discussion surrounding it can seem like angsty 17th century theology rather than rational speculation.
There is no “Great Silence” nor even a basis to imagine one; just a gap between theory and the capability of current instruments. The outlines of that gap may become more apparent once we can begin to sense exoplanet atmospheres in more detail.
Or…
While not the best equivalent example, this second is indicative of people fascinated with cryptozoology and continue to look for the Loch Ness monster and its ilk, the Abominable Snowman and the Sasquatch, and other mystical creatures like mermaids. It is also the basis of belief in the many gods of religions past and present.
As for your example, I would say that it is also a strawman argument. Most people I read do not say we must be alone in the universe because we don’t immediately see signs of aliens, but rather that aliens are not as obvious as the original SETI searchers they might be, and maybe much rarer than we thought, and even possible there are none. But I don’t read anyone stating categorically that there are none, which is rather different from the religious believers insisting that their belief’s god[s] definitely exist.
You seem to take it as a given that if we just observe for long enough, and comprehensively enough, the aliens will eventually be detected. As the OP makes clear, there is a 4th option, that the light cone of observation has not yet intersected with their presence. They are there, but the light of their presence hasn’t yet reached us. The 5th option is that the aliens are here, and buzzing about in plain sight if we would only recognize them for what they are.
In reality, there are very many explanations of the FP, not the 3 you advanced. Wikipedia has a more thorough list of explanations and of course, David Brin has waded into this subject extensively, a flavor can be gleaned from this interview with his view of METI.
It is better to consider these explanations (speculations really) as untested hypotheses that can in some cases be tested. For example, as per the Drake Equation, should our search for biosignatures come up empty, then one explanation for the rarity of ETI is simply that life is not common. The lack of radio signals indicates that the Bracewell “Galactic Club”, if it exists, is certainly not using radio waves that we can intercept, although the explanations for the lack of radio signals are legion.
However, contra your implied assumption, we should not rule out the null hypothesis either, that ETI does not exist, at least within our light cone.
Cryptozoology makes specific claims that run counter to large, well-characterized datasets. Whereas the notion that there’s nothing particularly special about our existence is the exact opposite of that, and overwhelmingly logical: It affirms that we can infer general principles from what we know specifically, rather than imagining that our circumstances are all that unusual. In other words, it’s no more logical to imagine that *we* are unicorns than to imagine unicorns.
Which is not to propose that the fanciful 19th century view of a cosmos teeming with our “peers” should come back, but I have no logical objection to a Milky Way we would consider “rich” in sentience if we had a representative glimpse. I do object to the idea that we would have found any of them by now simply based on scanning for radio signals for a few decades, like scanning a tiny angle of the horizon on a random patch of this planet for smoke signals….for half a second.
While it is certainly reasonable to imagine an average “time gap” between civilizational lifespans being a problem, we don’t really have much of a basis to put a number on that. As far as we know, civilization starts once and evolves explosively, leaping over regional apocalypses in the relative blink of an eye, and that argues for exactly the opposite premise to what Fermi falsely assumes to be evident.
FP asks why civilization hasn’t leapt across planets and stars yet. Obviously this is a loaded question that wildly exaggerates the relevance of present knowledge, and based on a premise that our datasets can’t even come close to justifying. Fermi is not a reasonable question even for the nearest hundred light years, let alone hundred thousand. We know practically nothing.
If one of the nearest exoplanets we already know about were a twin of Earth in every way, and had a technological civilization on it at or near our level, we would probably not be able to know that yet no matter how long we stare at it with current instruments and techniques. That very first step toward an answer still awaits the next generation of telescope beyond Webb, if not the one beyond that.
So far, SETI has only been able to rule out something it was never rational to suppose in the first place: That a superhuman civilization nearby in both time and space was so inconceivably high-minded and altruistic that they devoted significant resources to perpetually broadcasting across interstellar distances for just such an occasion.
But telescopes in this century should make a very preliminary observation toward a vastly more likely scenario, even if still a big ask: That there are (or were) technological intelligences within our sensing range that had done nothing to conceal themselves at the time their signal intercepts us.
In fact, even that will be a weak dataset, given the limitations of how we learn about other planetary systems in the first place (i.e., strongly statistical and based on things like viewing angle). In other words, the strongest negative we could likely achieve in this century would be something like, “The tiny fraction of all terrestrial planets within x light-years of Earth that we have been able to observe and confirm do not give off technosignatures.”
The fraction of Milky Way planets covered by that observation, even as a survey, will likely be minuscule. So FP wouldn’t even be justified by a negative result in that case. Contrarily, if we even find a biosignature…let alone technosignature…in this century, that would greatly increase confidence in what already seems intuitively logical: That we are not special in this galaxy or this era.
The fermi Question is not just about observing distant aliens, but why they are literally not buzzing about now or in the observable past. [UFO enthusiasts feel they are if only we would accept their explanations.] As you well know, there are lots of explanations put forward as to why ET is not on Earth or chewing up our system for resources. However, it is also not unreasonable to ask why these explanations seem to bear a remarkable similarity as to why the deities of all religions are invisible to almost all humans too.
Cryptozoology isn’t just about fantastical creatures like unicorns. Living fossils are also a target. Sometimes they actually are discovered, e.g. the coelacanth. Remarkably, new species of largish animals are discovered almost every year, although vastly outnumbered by newly discovered invertebrates.
You are using what I would consider an overly expansive definition of cryptozoology. In the more traditional definition it is remarkably similar to ufology.
“The fermi Question is not just about observing distant aliens, but why they are literally not buzzing about now or in the observable past.”
That’s mostly about people not grasping the scale of space, even within the solar system let alone the galaxy. Even Earth is just barely inhabited by the standards of a Type I, and all our vaunted cities little more than isolated archipelagos.
By far the likeliest whole number (i.e., >0) of people to have set foot on any given square meter of Earth is 1. You would have to go very deep into developed areas before it becomes 2.
With that understanding, the likelihood of “visitations” to Earth would be vanishingly low even in a galaxy where every habitable planet is inhabited by sentience. In a galaxy where sentience is common but not ubiquitous, the likelihood would be vanishingly small even compared to that.
Space is just too big. People don’t even explore their own back yards very thoroughly, let alone the meadows just outside of town or the wildernesses beyond. I don’t know why they imagine other species would be any different on scales unimaginably vaster.
I agree with you that visitations should be very rare. But then, by definition, all those encounters with UFOs buzzing around in the skies cannot be real.
As Clarke suggested in 2001: ASO, the visitors might only have time to visit a world once to plant the seed for Mind, never to return, just leaving their machines to monitor progress. Fermi’s question includes the apparent lack of evidence (so far) of any visitations even in deep time. If ET visited, it was with a light touch, or maybe we just cannot recognize what they did, assuming all phenomena are natural. A lurker, much like a buried lunar monolith, would be evidence of visitation, even if only by a machine, rather than biological beings.
Now if technological ETs have personal vehicles like autos that can easily traverse interstellar space, then trillions of such vehicles visiting primitive planets as if on safaris, might allow for craft to buzz about in teh skies. I don’t this that is the case, but…
That’s an interesting argument. Imagine a family of arctic voles living somewhere in northern Canada. They say to themselves, “Well, we’ve been looking around for a couple generations and haven’t seen any humans so humans must not exist, or they must not be able to travel across the entire world.” In fact, the answer is just that no human is interested in going to that particularly undesirable piece of real estate.
So possibly it comes down to fallibility. Are ETs fallible as we are? And if so how fallible? I could think of a fallibility index. Possibly most intelligent beings have a fallibility around 0.5 (where 1 is completely infallible and 0 is always fallible). I believe we are an average intelligent species with a fallibility index very close to 0.5. If we fail as a species then probably our place on the index was below 0.5. And at what point in the index are a species absolutely destined to destroy themselves? Or put another way, where does a wildly successful species with little or no self-destructive tendencies fall on the index and how often do they arise? And we also have to take into account accidental destruction such as by a large impactor strike before we are sustainably off-world or before we can reliably deflect an impactor or any other massive planet-wide disaster. So possibly intelligent life is rare, also fallible to some extent, and also subject to the vagaries of the physical universe and so ETs that are so successful that they can conduct huge physical expansion are very, very rare (possibly less than 1 per galaxy).
Thank you for the post. The title is certainly true, almost an identity.
Exclusivity is only an issue if populations are high enough and the pool of motivations is small. It wouldn’t be uncommon for a selection of 10 people to contain no swimmers. Motivations can be weighted to occur more often, spreading to new environments is a heavily weighted motivation for Life. However, the potential to be weighed does not rely on anything covered in the “Exclusivity dilemna”. The “Exclusivity dilemna” contains too many hidden assumptions to be useful as a counter argument.
One Space Faring Intelligence will not fill a space to exclusion by decision alone. The Milky Way wouldn’t reach exclusive densities unless that SFI could practically replicate the motivation an economics 100-200 billion times over many millions of years. Facing a pool of motivations stretching beyond our conceptional horizons, exclusive densities are hard to take seriously as the default.
Elephants and termites can be used to analogize how easy it would be to find evidence of different SFIs. Assume two real world savannas, each able to support but not optimized for either elephants or termites. Grant both animals the ability to transform their space without competition. Termite mounds would fill their space, exclusive densities could be reached easily. An observer dropped into the space would quickly identify the dominant life form. Elephants also dramatically transform their space, but exclusive densities are less likely. An observer dropped into the space would have to work harder to find evidence of elephants. The spectrum implied with this analogy would map to that implied by footprints left by SFIs that spread system by every system and remain or move system by system.
Technology is a necessary and transformative ingredient of the Space Faring Intelligence. It may be very hard to resit the transformation. The draw of becoming the most complex consciousness technology allows must be great. K1 individuals are possible. The likelihood of resisting does not insist upon the resistors reaching exclusive densities. Resistant to transformation may include resisting space travel and contact with their space faring cousins. I would expect the SFI footprint would be concentrated against the envelope provided by technology. Biological SFI could persist but may be wary, their biological nature leaves them more vulnerable to threat or influence. Wary for the benefit of themselves as well other biological SFIs.
Several of these posts made arguments for some facet of alien behavior being universal. I call this the Universalist argument as a shorthand.
Neither Dr. Hanson nor I, subscribe to the Universalist argument. Dr. Hanson bases his paper on the assumption that aliens will have a wide variety of behaviors, most of which will render them hard to detect, but one sub group, the expansionist colonizing variety will be detectable. He even looks at the consequences of variation in their frequency.
I think that a variety of alien behaviors should be the working baseline assumption, mainly from what admittedly is the thin evidence we have for variety, and from our general observations of how the universe operates. Also, the variety argument is not really an argument. It is the no-assuming assumption that anything is possible, and to put any constrain on it, you must make an argument to support it.
This does not mean that universalist arguments cannot be made, but they must be justified with solid logical inference or some evidence pointing in that direction (data would be really nice, but given the way the field is that’s generally not possible).
To give an example, the Universal transcendence speculation, which is that after a certain number of years all technological civilizations transcend to some non-detectable existence, putting a limit on their lifetime detectable footprint. This idea has the backing up by models as an explanation for the lack of visible aliens. So far-so good, but what universal reason is their for this behavior? You can’t answer the question by making another assumptions. And, is there any evidence to support your assumption?
To take the opposite tack–that most technological civilizations will be expansionistic and colonizing–as they are founded by intelligent life, that has supporting evidence. Life has expansionist and colonizing behavior. This is due to evolutionary selection. And it is assumed that the laws of evolution are the same throughout the universe because at base evolutionary selection is due to a quirk in the way that entropy works. And if entropy varied throughout the universe, it would affect our cosmological models and observations.
The idea of transcendence is problematic, especially as it has religious connotations of an eternal afterlife.
However, consider that all other organisms have (as far as we know) no knowledge of an afterlife. Their physical expansion is limited to reproduction and inhabiting any new space that becomes available.
Humans, however, are able to conceive of an afterlife, however, that is made available. If it is available technologically, that seems like a likely avenue for those wishing to have non-corporeal bodies, especially if that comes with abilities to traverse space and live in a much deeper time. This is how a mental expansion can occur, and while not driven by the algorithm of natural selection, is one driven by individual agency. Our more near term option, if possible, is mind uploading into a computational matrix offering an infinite variety of simulated spaces, conceivably greater than available in the universe. In this case, aliens would remain “quiet”, existing within an artificial construct. They would not be expansionist in the physical sense, but rather in simulated space. While the simulating computer could be detectable, it might well be limited to the homeworld, or relatively few systems, and would therefore remain undetected for some time until the technology appeared that could detect it, or, an expansionist species discovers it.
Now I don’t want this to be a case of universality, simply that when intelligent, technological species do emerge, those that decide to become expansionist in simulated environments reduce the number that will opt for physical expansion, ensuring that the Fermi paradox appears intact through the very rare emergence of such “loud” species.
For biological humans, with our short lifespans making interstellar travel very difficult, we already travel to the stars in mental simulations – stories in various media. We are already moving towards partially living in simulated worlds. Transferring our minds completely into thiose simulations would allow anyone to explore any number of worlds almost instantly, and with a length of time unlimited by biology.
Having said that, humans also want to explore real spaces too, so maybe that sub-population will choose to be physically expansive, as will ETCs with a similar desire.
Trans-humanism can be driven by the algorithm of natural selection. We just have to make the fairly safe assumption that transformed beings will have advantages over those who don’t. In space the space environment, this is easy.
Isn’t that unnatural selection, like animal breeding? Darwin’s pigeons come to mind. But I understand your point. If human civilization collapses, then over the long term, the enhanced humans will either spread their genes into the population or they might disappear, as natural selection indicates. It will depend on the purpose of the engineering and the success of the phenotypes to replicate in changed conditions.
There is ample evidence of intelligent beings, including non-humans, applying technology to increase agency and general fitness. Transendence would be driven by mundane competition and a Space Faring Intelligence that embraces transformation will be more fit for space.
There is plenty of evidence of Life expanding and colonizing, I am not making a case against expansionism. With that evidence is there any need for the “Variety principle”? We can make the case that any motivation is theoretically possible but can we make the case all motivations will exist. The latter is how I usually see the variety principle being used. Including here.
The broader the spectrum of hypothetical motivations the smaller the percentage of that spectrum we should expect to see in practice. Unless, of course, we assume the population of Space Faring Intelligence is as large as the spectrum and evenly distributed among motivations. I think that is unlikely. Perhaps it is more practical to assume populations cluster around the most fit motivations.
I would also argue your formulation of the “universality dilemna” is itself problematic. Assume a population 0f 10 selected from a much wider spectrum of potential motivations. All 10 individuals have a unique motivation but the motivation labeled orange does not appear. Are those 10 universally exhibiting not-orange motivations?
My idea was any civilization with FTL technology can go anywhere very fast, so they don’t need to colonize another world which would make any need for expansion completely superfluous. I assume that 1) the power problems have been solved for very power efficient space travel technology as well as home world energy infrastructure. I think the universal transcendence idea might only apply to a ETC that is over one hundred million years than ours which is the time when most ET worlds move out of the life belt of G class stars. I also assume that any civilization which is a million years more technologically advanced than ours has FTL, a conversion based physics. Any ETC would still be detectible with a spectrometer. The oxygen in our atmosphere has been easily detectible for 500 million years since the Cambrian explosion, but only easily detectible with a ETC that has the technology. We still are just beginners at that.
According special and general relativity, anything outside the light cone can’t be seen from someone from inside it, so any spacecraft FTL would be completely invisible. I did not mean an ETC home planet is invisible. There cities still might have lights.
Universality is not mutually exclusive from uniqueness. Universality in philosophy includes all outcomes and possibilities. Science, physics, chemistry and genetics don’t work without general principles. Both opposites should be included. I agree that uniqueness should be considered, however, I would not go as far as saying that our behavior must be completely different that ET’s which might be dependent on the level of psychological advancement or level of consciousness of the ETC, i.e, one much more advanced that our might be more civilized as a whole or collective than ours prognosticating our future potentials.
I don’t equate a religious view with being naive just a different one or non physical view, the unknown can be extrapolated based on one’s knowledge base and level of consciousness, for our physics and technology today would be considered complete magic to anyone from the middle ages. In order to extrapolate into the future, we must use what is the highest level of understanding today which can include a viewpoint which challenges the conservative past. Also our eyes are limited to the visible spectrum which is only a small portion of the electromagnetic spectrum. Science and physics require also abstract thought and require us to have instrumentation or extensions to our senses beyond the visible and not just what matches superficial observations. Being isolated, it is easy for us to think we are the ultimate and there is nothing else out there.
” Life has expansionist and colonizing behavior.”
Self-awareness frees you from the impulses of instinctual behaviour. Humanity already is limiting its own expansion and in fact has retreated from habitable environments in the name of conservation and biological diversity. Technological progress will likely mean further options on choosing what facets of biological imperatives we as a species select to pursue. The discussion on civilizations mimicking life on bacterial level so to speak has been present for a long time, and convincing argument for either side can only be made with some support of evidence, hopefully in near(in human life time) future, based on telescopic observations.
Hi Dave Moore & Paul
It’s possible we don’t see expansionist civilizations because some property of our Universe, which all potential expanders observe eventually, causes the strategy to change. Perhaps they gather evidence for a Cosmic Collapse in a few aeons and thus bail out of the cosmos via SMBH wormholes, or they go dark to await the end of the stellariferous era to start proper colonization efforts of the neutrino-capture warmed iron-core planets that will form from supernova debris?
It’s possible, but by the rules of reasoned argument, you must i) substantiate your case with some sort of evidence, or a solid line of argument, and ii) because you postulated a universal, you must also make a case for this behavior being universal in expansionist civilizations.
This is why I think the best approach to SETI is to work along lines that make no assumptions about alien behavior.
Hi Dave
One problem. Evolution. Hanson’s model depicts AEONS of expansion. I don’t believe species or clades will be so uniform for so long. That’s almost certainly Universal. There will be Statics or Parasites appearing within those volumes. Perhaps they’re bubbles of expansion, hollowing out from within as Grabby Aliens become Non-Grabby or extinct. Given the lightspeed limit, exponential growth *will* become impossible in a finite time. So it will become an Expansion wave or bubble, at best. The Frontier will be a thin hollow shell. Throw those inevitabilities into the simulations and it’ll be a very different looking temporal evolution I’m sure.
If the civilizations expanding at the frontier (bubble surface) do not exhaust every resource behind them, then as on Earth, new grabby civilizations may emerge inside those bubbles and form new ones. Or a grabby civilization inside the frontier becomes quiet again for a while until a new grabbiness emerges to start a new bubble. This model results in lots of new expansions inside the first expansion. It may even be that the new bubble civilization expands faster than the earlier one and overtakes it.
While these models produce interesting outcomes, the fact is that we do not see any signs of these expanding civilizations anywhere in the universe, something that we would expect if they were all following the race to be moving from KII to KIII status. Wouldn’t we see zones of IR in other galaxies, indicative of a wave of colonization surrounding stars in Dyson swarms? We have a lot of galaxies to sample to tease out examples even with the lowest probabilities.
[Maybe dark matter is just a lot of stars that are being fully harvested for their energy that are located outside the galaxy in the relative safety of intergalactic space. ;) ]
As our technology improves, we should get better at detecting signs of these expanding civilizations. Either they are there and we have yet to create the needed tools to observe them, or they do not exist and the FP becomes a question concerning the whole universe unless ETCs have only just begun to emerge after a long gestation.
There may be several ETIs and each has a different reason we have not detected them.
We’ve found some hypervelocity stars; maybe ETIs wanted them to move very fast out of our galaxy, so they could be alone in intergalactic space, and the stars are taking a whole bunch of habitats with them.
Some ETIs might be colonizing only dwarf stars, or only rogue planets, or only black holes.
One argument against the likelihood of ancient Earth civilizations is that they didn’t use up all the mineral wealth we’ve been using. But some of those resources could have been replenished some time in the past (how many millions of years ago?)
Or the previous civilization politely put the resources back into the ground for our use, once they had advanced to using other resources.
Or they *only* used up the resources in one region of the world before advancing to space flight and abandoning Earth.
On a related note, those UFOs might be from an advanced ancient civilization native to Earth or elsewhere in our solar system…or native to Scholz’s Star…
I’m not taking these possibilities all that seriously, just brainstorming.
We can be fairly sure that some ancient civilization didn’t mine out the carboniferous coal beds as we are finding them and can trace the beds in the geological strata. As for putting minerals back, that was awfully costly to disperse metals and other minerals in slightly concentrated form in the rocks. This sounds very like “God/Satan put the fossils in the rocks to fool us.” ;)
The whole idea of colonizing stars is so reminiscent of the European colonization that we now say we abhor. This wasn’t because species naturally expand, but for political and resource control. The British empire was all about the control of local products that could be transported back to Britain. IIRC, the American colonies were not allowed to manufacture goods that were made in Britain, ensuring a supply of revenue to Britain.
Driving one’s homeworld star out of the galaxy to be alone might make perfect sense if there is a predatory species in the galaxy. This is very anti-colonial and akin to making a nation very difficult to invade.
An increasing energy use since the mid 1700s has been one of the hallmarks of the industrial age. It could point to a Great Filter. A filter that may elsewhere be avoided by innovations and technology that avoids the massive increase in energy use. Similar considerations may apply to the environment including the biosphere.
Biological imperatives look to immediate gain. Parsimony rather than profligacy is more a function of the intellect/intelligence, but may spell the difference between extant and extinct.
“An increasing energy use since the mid 1700s…”
Your very perceptive comment provoked an unexpected speculation on my part.
The widespread use of steam technology in the late 18th century is what sparked our extreme exploitation of energy. We’ve had water and wind mills, sailing vessels and muscle power since ancient times, but the industrial revolution was made possible, if not inevitable, by fossil fuels, particularly coal in the 19th century, and petroleum in the 20th. Even if combustion is only the initial energy tech, eventually to be replaced by something else, I find it hard to imagine how our technical civilization could have arisen without abundant and accessible fossil fuels at the beginning.
Is the geology that laid down these carbon deposits likely to be a feature of all, or even most, habitable worlds? If the geological processes that have preserved the carbon of ancient life forms does not occur on all suitable planets, then technical civilization may be very rare indeed in the Galaxy, even if intelligent and civilized species abound.
Unless one accepts Thomas Gold’s theory about fossil fuel creation by organisms slowly extracting hydrogen and leaving carbon, then the contemporary explanation for coal is the fossilization of plant material during certain periods, like the Carboniferous. Only natural gas could be abiogenic, probably primordial, although biogenic creation also occurs.
If civilization power sources transition from human muscles to animal muscles, to wood (trees), wind and water power, and then to coal (oil seeps seem rarely used except for lighting), then unless evolution and climate development result in the creation of swamps and eventually coal production, then there could no transition to steam power. A counterfactual is that the Greeks did create a crude steam engine (Hero’s Engine) although not a practical power device, the mythical use of polished shields to ignite a Roman fleet (solar thermal power), and the current use of peat, an industrial revolution may have occurred without coal. Prior to the use of coal, Britain cut down most of its forests to create charcoal, but it required the greater energy stored in the coal beds to drive the industrial revolution. There is still hundreds of years of coal to power our civilization, although there won’t be much of a civilization left if we go that route. If solar thermal power could have been developed more extensively, and synthetic fuels manufactured as fuels, just maybe an industrial base could have been supported using solar power, a direction we are currently going towards but with solar PV.
Hi Alex,
Perhaps we should follow up on this line of thinking. Please consider my post in response to Robin Datta below. It may be whatever made large deposits of coal and oil available to us (the contribution of plate tectonics to the compression of coal beds and the concentration of petroleum fluids?) is a necessary (but not sufficient) condition for the flourishing of hi-tech civilizations.
It is speculated that the fungi that now decompose wood had not evolved when beds of wood laid down in ancient forests were subducted and “pressure cooked” into coal. Wood now promptly (in geologic time scales) decomposes, and peat, a precursor of coal, persists because it is past the susceptible wood stage, although it has not been “pressure cookod”.
Petroleum comes from algal beds that had similarly been subducted and “pressure cooked”, with overcooking producng natural gas.
Both processes do need the appropriate geology and biology operating in an appropriate temporal sequence.
Perhaps solar and solar-derived (wind, water, etc.) energy sources could permit some industrialization, as was the case with various mills at rivers in the nineteenth and early twentieth centuries, (hence the term “mills”) but they were promptly abandoned when fossil-fuel derived power became abundant.
Of course speculation now turns to sail power for interplanetary and interstellar travel.
This discovery of fossil fuels did not allow us to do anything we couldn’t do before, but it did give us the capability to do it on a much grander scale. For example, we made steel sword blades using wood charcoal, but it required lots of coal to make steel in industrial quantities, or to make railroads and steamships practical. I really think we need to give some thought to the “bottleneck” effect implied by civilizations arising on planets where coal and petroleum were simply not available.
On the bright side, perhaps there are other sources of high-density, abundant, easily accessible energy sources available to young technical civilizations ‘on the way up’ that might substitute for coal/oil on planets with alternative biology/geology. Maybe on some worlds, alcohol from fermentation plays the role of hydrocarbons here on earth.
We spend a lot of time theorizing on things which might help or hinder an up-and-coming technical species (like an opposable thumb, or the lack of it) but it occurs to me that just living on a planet where high-carbon fuels are naturally available is one that has been neglected in our speculations.
It may turn out that the lack of plentiful fossil fuels will prevent cultures from developing an industrial/scientific revolution.
Historically speaking, Newton and Watt were practically contemporaries. Perhaps without the second, the insights of the first would have been irrelevant.
Brian Cox is interviewed on the UK’s Sunday Morning show. Asked about ETC in connection with UAOs and he said that there might, based on terrestrial biology, on average, be less than one per galaxy, or perhaps a few. Given there are 2 trillion galaxies, that leaves open a loophole to allow UAOs to be aliens. But I don’t think we need to accept his argument from authority, He is definitely in the idea of life (microbes) are common, but intelligent aliens are exceedingly rare.
I do like his perspective that we might be the only intelligence in the galaxy, and the responsibility that implies. [And that kiboshes any conspiracy theory that aliens are trying to destroy humanity by bringing the 4 horsemen of the apocalypse (conquest, war, famine and plague) together right now. It was a confluence of catastrophes that collapsed the Bronze Age Mediterranean civilization around 1200 BCE.]
We have seen what happens to expansionist empires on Earth. They rise, expand, and then collapse for one reason or another (competition from other expanding empires, governmental instability and collapse from within etc.). Why would it be any different for ET’s attempting expansion? They run into something that defeats their expansionist tendencies or they rot from within. Are these universal tropes? If we manage to expand outwards in thousands or tens of thousands of years by a slow process such as ark ships containing humans or frozen embryos, or something quicker such as sentient machines in faster ships, we should find out how big our expansion bubble can become. If we’re alone as a sentient species in this galaxy that leaves a lot of territory to inhabit. Are we stable enough as a species to take that on?
Also the exhaustion of natural resources, e.g. exhaustion of agricultural land, or some critical resource due to internal factors, or external ones, such as climate change.
There are many potential answers, but the one that appeals to me most right now is that the aliens don’t use EM radiation to communicate. There is simply some other thing that anyone who understands a radio will figure out in a millennium or less — something that carries higher bandwidth, avoids interstellar dust and the noise of nearby stars, which can be sent person-to-person without the whole planet having to agree on a message, which uses vastly less power, and/or arrives instantly (if not sooner). Given that we have no idea what most of the mass and probably most of the energy in the universe is made of, this seems hard to rule out at present. Any specific group of aliens probably won’t get their ducks in a row to send loud long-range messages before they discover this medium better than light. But they *could* still choose light to speak with very early civilizations … just as people could fish for trout by going out and capturing fingerlings to raise in a home aquarium. I think there is a chance that is comparatively unlikely on the cosmic scale.
On the other hand, I could also observe that the human immune system stops many cancers before they have a chance to become established.
This would argue for looking for physical artifacts, like megastructures, or some change in their planet’s emissions.
This approach to the Fermi question certainly provokes thought.
Going back to the early part of this presentation, the notion that several events leading to ET civilization ( or ours) resemble the divergences of biological systems affected by cancerous growth – it has a plausibility.
The plausibility being our own recorded or identifiable history. Especially when we index our energy generation, both the consumption and the waste. Because once we start consuming energy at high rates, it is a difficult task to maintain the control. We observe geological time, but we have little experience in engineering for it. Hence it is hard to speak for the experience of other civilizations with Kardeshev levels of energy production. But if we were to communicate anything to them, we might start with Malthus…Or ask if they had ever tried playing poker and continuing to double the ante. How did it go?
Also, spontaneous generation of life got a bad rap back here on Earth when it was observed that maggots did not form as prolifically around rotting meat when there were screens surrounding them that flies could not penetrate. This did not necessarily mean, however, that life did not have special properties. After all, we are surrounded by carbon and carbon compounds, but there are distinctions between living matter based on carbon and inert matter which is not living. And then with all due respect to Mary Shelley, there is resuscitation that restarts a heart and then there is electrical shocking of dead matter that is not going to get a response, such as “Hey, would you cut that out!” If consciousness and sentience were never there in the first place, bolts of lightning are not likely to provide it. Very, very unlikely. Unless we are missing something.
Which takes us back to spontaneous generation. For isotopes, we know that there are decay rates and the statistics of these for isotopes are very precise. And yet we can’t predict when a particular nucleus will break down and decay.
What’s my point? The fact that stellar interiors produce carbon and distribute this and other atoms into the interstellar medium where it can accumulate on planets indicates that the universe is not entirely hostile to life. But it is hard to tell how favorably disposed it might be.
After all, Stanley Miller’s experiment showed how biological precursor compounds could form, but it did not proceed to Mary Shelley’s expectations. It could be that “life” generates more like a beta decay than from a lucky lightning bolt in an infinite progression. And there could be a medium within galaxies that effect the odds of it recurring, say, from star to star or planet to planet.
The process to sentience is a long road and I don’t have any idea when it is crossed. Somewhere there’s a difference between communicating a signal such as on or off and telling how one feels… But advancing to the issue of civilization and power generation, our early exploits are based on combustion and fire. Were we all aquatic, this could pose a problem. At the very least, our history would be different, and even with talking like or better than whales, we might not get around to it for several million years. Using whales, of course, is a terrestrial illustration, but oceans elsewhere might not have anyshores or air above them. Now this might even be a significant consideration just in accordance with the range of exoplanets we have discovered so far. “Land” might be an unusual concept whether there is life or consciousness or not. If your world were as big as Jupiter and you ( an ET) had access to tens of kilometers of its depths, would you really be that concerned about what is going on in the galaxy? Or the solar or star system? There might be circumstances. If things were alive and sentient, it is hard to imagine to what energy sources they might have access.
Coming from this direction and looking at Fermi’s question or Drake’s equation, there are other ways we could set up the relations. But perhaps one of the difficulties is the role of Earth analogs. What are truly necessary planetary conditions to provide a life form to enter into such a sweepstakes hundreds of millions of years after planet formation or even later?
It’s been argued that the scientists who supported spontaneous generation were actually the progressive ones of their time. They were trying to figure out how life could originate naturally from non-life (what we now call abiogenesis). According to this argument, opponents of spontaneous generation e.g. Pasteur were religious and political conservatives. They wanted to show that life could not have originated naturally from non-life, but only done so through some non-natural event e.g. divine creation. It’s an interesting alternative take on science history, although probably open to debate.
Doesnt all the math require a n larger than 1?
Conversely, is not the denominator of 1 example of 1 civilized planet to every X planets growing rapidly with the advance of astronomy?
It is still early, but the universe does not appear “fine tuned” for life, or else it would be reasonably abundant.
The discussion so far seems mostly confined to our galaxy and the uncertainties of the step function probabilities plus the light cone constraints on observing expansion bubbles. Given that, let’s widen the sample size. The universe appears to be 13-14 Gy old. With trillions of galaxies there should be enough examples of expansion bubbles of grabby aliens. So far the only expectation was that such ETCs would move towards capturing energy with Dyson swarms. Yet the GHAT survey showed no sign of extensive Dyson swarms in the sampled galaxies.
IMO that implies that any grabby ETCs do not expand in the mega engineering way. If they do colonize, it is far less evident. Alternatively they remain “quiet” as they have an expectation that predator ETCs exist, and these predators also stay hidden as terrestrial predators do, rather than human conquerors with huge armies.
If either is the case, we cannot expect to build our KII civilization around Sol as an energy hungry one. If so, we need to look for different evidence of ETCs, loud or quiet, bearing in mind they may be camouflaged.
The last possibility is that we are alone in the universe as the most simple reading of the FP implies. If we value Mind, that is an awesome responsibility for humankind, yet it offers a tabula rasa for our future should we take it.
@Alex Tolley:
What is your intuition telling you about the commonality or lack thereof of life in the Universe? Obviously, we need more data– just wondering what your “hunch” is on the matter…
“In a typical run with parameters resulting in them not being visible to us, expansive civilizations now control 40-50% of the universe, and they will finish up controlling something like a million galaxies when we meet one of them in 200 million year’s time. (Note, this paradoxical result is due to the speed of light. They control 40-50% of the universe now, but the electromagnetic radiation from their distant galaxies has yet to reach us.)”
Based on the above quote, does this mean we would not see its techno-signatures until the expanding ETC was relatively “close”?
I don’t buy that the limitations of c mean we haven’t seen them yet. As this site has posted before, we can expect there to be very ancient aliens in the universe by now, as they have had 3x the emergence time as Earth has had life. So we should have seen physical of them in other galaxies billions of ly away by now – yet we don’t. If they are there, they don’t appear to be fully trapping the energy of stars in their galaxies. Of course, they could have emerged and then gone extinct, say over 1 million years, so that they might be like popping light bulbs, observable for just a moment, then gone, and with them their megastructures. If ETCs exhibit all sorts of behaviors, this should include such megastructures, so why don’t we see any? I find it hard to believe that ETCs have only emerged recently in the universe, and allowing c to hide them.
Whatever my hopes for life, biological or machine ETCs, I would prefer to see some data, particularly biosignatures. If the sky is bare of these, then we have to revise any hope for life being ubiquitous, and that surely impacts our estimates of the presence of ETI. However, the converse is not true, as the emergence and sustainability of ETCs to reach starfaring status may be extremely difficult, with the Great Filter ahead of us, not behind.
“Yet the GHAT survey showed no sign of extensive Dyson swarms in the sampled galaxies.”
There are several Dyson swarm surveys and most have possible candidates.
For example:
https://technosearch.seti.org/optical-list/optical-and-radio-searches-dyson-sphere-candidates
” 33 Dyson Sphere candidates with excess 12 micron radiation no 60 micron excess ages greater than a gigayear were observed for SETI signals with the Leuschner Optical Telescope, SERENDIP IV at Arecibo and the SETI@home program. Stars were observed with measured ages of above 109 years, such that there is no protoplanetary disk, a known source of infrared radiation. This search is significant enough to warrant further investigation. [Data were taken with OSETI pulse detection system at Leuschner, and SERENDIP IV and SETI@home systems at Arecibo Observatory]”
There are two issues here, first of all you can’t really confirm them as artificial, they might very well be normal celestial objects such as brown dwarfs.
Secondly, the other surveys were looking for galaxy wide Dyson swarm settlement, which seems inconvincible; there is no need for such extensive colonization and probably better energy gathering methods exist, plus limits in communication using light speed mean no realistic unified command or culture can exist on such a scale.
Universality is an erroneous dilemna. We don’t have to solve for every hypothetical ETI, only those that actually occurred. Anyone who wants to argue against practical universality has to make the argument that all possible ETI types exist.
We also don’t need one ideal explanation to the Fermi paradox. We would get the same results if there were an unique reason for each ETI type. The Fermi paradox may even be better explained by multiple overlapping reasons.
We don’t need a universal reason to prevent grabby ETI behaviour. Ad hoc reasoning does the same work. The quest for The One reason is mostly aesthetic or competitive. Unfortunately we have no idea who else showed up, if anyone.
Abuse of the Universality dilemna is a pet peeve of mine. Please forgive what may look like harping on the subject.
Assume a sealed box containing 9 orange stones and one 1 black stone. The orange stone represents something that would block grabby aliens, the black has no effect. All members of the grabby population must choose a stone. The box manages a hypothetical, 90% block effectiveness. Would it be unreasonable to assume all members of a population of 9 grabbies is blocked? What about a population of 100 grabbies? How high does the population have to be before we need an explanation besides the ratio of orange to black stones?
Change the ratio of stones so that there are fewer blocking stones, but assume all grabbies need to draw from multiple boxes. This set up could easily eliminate a huge population of grabbies without ever relying on a universal, 100% blocking mechanism.
Personally I await the arrival of the noisiest, most grabby of aliens, the Vogons with their constructor fleet (also the third worst poetry in the universe) with some trepidation.
Just check out the plans on Alpha Centauri to see when they might show up.
I keep my towel handy at all times – just in case.
I am somewhat amused by the paper and its conclusions. You often find the same assumptions in such theories that amount to:
-civilization as a bacteria or in this case cancer rather than a construct by self-aware beings
-non-ending expansion(in this case stopped by neighbours)
-we can’t see them, haven’t seen anything
Now all these assumptions have been deconstructed several times.
For instance there is no need for civilization to constantly expand, in fact the limits of light speed for communication mean that besides clusters or very long lived/hibernating civilization vast interstellar empires of same culture are impossible. Likewise the abundance of resources in single solar system means that a civilization counting billions if not trillions could safely exist in it for millennia if not more. At the same time technology makes the reproductive imperative malleable and even unnecessary.
http://astro-ecology.com/Astroecology_Human_Space_Populations.htm
“Based on the limiting elements N and P, water-extractable materials in one kilogram of carbonaceous asteroid soils can support 0.6 grams of biomass. On this basis, bioavailabe extractable materials in the 1e22 kg carbonaceous asteroids can support 6e18 (six million trillion) kilograms of biomass, six thousand times more than the biomass presently on the Earth, that supports six billion humans. The extractable asteroid materials could then support on the order of 40e12 (40 trillion) humans. Using the total elemental contents of the carbonaceous asteroids could support a biomass and population a hundred times larger yet, 4,000 trillion humans, comparable to the population of a million Earths”
The other point, of them not being visible, therefore not existing is nothing more than a fallacy.
First of all it only amounts to the conclusion that there are no vast existing clearly seen civilizations. The argument “it only takes one civ to colonize whole galaxy” only means there isn’t one, not there are none civilizations at all.
Second of all, how can you be sure you aren’t seeing one? Contrary to popular belief SETI didn’t come empty handed, it only came with inconclusive results, and with no evidence of any directed signal. For all human arrogance, we aren’t really that advanced technologically, and we (barely) made it only to the Moon orbiting our planet. Our telescopes can’t even image planets around nearest star to the Sun, never mind signs of other civilizations if they exist. For the record there are actually several papers on Dyson Spheres with numerous candidates-but they all come down to the fact that none of these candidates can be distinguished from natural objects using current technology. We know of things such as hypervelocity stars, Przybylski Star and countless other phenomena that will take centuries of development to fully understand. For all it’s worth how can you be sure that Hoag’s Object isn’t a work of galaxy spanning civilization?
The bottom line is that we need to gather more data and observations before coming to radical conclusions based on pure abstract logical games that might be detached from actual state of things. Hopefully the coming age of new improved telescopes will at least give us a small glimpse into composition of exoplanets, atmospheres and potential biosignatures upon which we can start building more realistic assumptions.
http://seti.berkeley.edu/exotica/
https://iopscience.iop.org/article/10.1088/0004-637X/698/2/2075
https://thevoroscope.com/2018/07/18/is-hoags-object-an-engineered-galaxy/
https://www.tillett.info/2016/08/03/carnot-efficient-dyson-spheres-are-undetectable-by-infrared-surveys/
” If Wright et al. had assumed Dyson spheres are 0.99 (or better) Carnot efficient then their emission spectra would not be detectable above the background infrared emissions of interstellar gas and dust – put simply, the emission signal from efficient Dyson spheres will be swamped by infrared noise in any wide-field infrared surveys. Unfortunately this means that all we can conclude from Wright et al. study is that there are few (or no) Dyson spheres built with a 0.95 (or less) Carnot efficiency. If Dyson spheres do exist, and they are efficient (which we should expect of any advanced civilisation capable of building such spheres), we won’t be able to spot them via infrared astronomical surveys. “
“So we should have seen physical of them in other galaxies billions of ly away by now – yet we don’t.”
Take your pick:
https://en.wikipedia.org/wiki/Hoag's_Object
https://en.wikipedia.org/wiki/Great_Attractor
https://en.wikipedia.org/wiki/Axis_of_evil_(cosmology)
https://en.wikipedia.org/wiki/Fast_radio_burst
https://scholarworks.umass.edu/astro_faculty_pubs/304/
https://www.universetoday.com/80955/red-dwarf-discovery-changes-everything/
“For years astronomers have assumed that the number of red dwarfs in any galaxy was in the same proportion that we find here in the Milky Way but surprisingly the study revealed there are about 20 times more in the target galaxies. ”
https://academic.oup.com/mnras/article/478/2/2541/4992331
“We have serendipitously discovered that Leoncino Dwarf, an ultrafaint, low-metallicity record-holder dwarf galaxy, may have hosted a transient source, and possibly exhibited a change in morphology, a shift in the centre of brightness, and peak variability of the main (host) source in images taken approximately 40?yr apart”
” If ETCs exhibit all sorts of behaviors, this should include such megastructures, so why don’t we see any?”
How do you distinguish a megastructure from natural object using today’s observational technology?
Thank you for these 2 comments with links. I was particularly interested in the issue that very efficient Dyson spheres would be indistinguishable from the background IR.
Posit for a moment that an expanding ETC is indeed capturing all the energy of the stars by such devices within the bubble of their expansion. Wouldn’t that be observable by a missing patch of luminosity, yet with an output shifted to the IR, in a galaxy? I appreciate that this might be similar to an obscuring dust cloud or other natural phenomena. OTOH, there might be ways to distinguish between such natural phenomena and artificial ones.
I disagree about your comment about the spatial impossibility of a galaxy-wide civilization. You are making the assumption that such a civilization must be cohesive and coordinated on a temporal scale that is far shorter than the communication lag across a galaxy. This needn’t be the case. Before the invention of the telegraph, coordination across global empires was very slow, albeit still well within the lifetimes of the central agents issuing commands. Civilization can be more than this – for example, an idea that instructs a way of life. Western Enlightenment can inform independent nations to act in a consistent way without requiring coordination. As usual, one must also accept the possibility that FTL communication may be possible, even if we have no idea how that is possible.
> If the civilizations are out there, but are invisible to our current instruments, then a much broader variety of distributions is possible.
This is a pretty big “if”, imo.
I would just like to point out that the essence of this paper is not what aliens could be, but what they cannot be.
This is useful in that it limits the speculative area of what the could be.
Reading thru the comments I realized just how backwards we really are. We assume that they do it the same way we do, pun intended! We need to put our heads where they are, 10,000, 100,000, 1,00o,000 years ahead of us, for the ones we may be able to understand.
These civilizations have arrays covering the whole electromagnetic spectrum both to transmit and receive. They are broadband in the fullest extent and transmit messages on all the frequencies that can travel through space without impedance. Why would they do this? For the simple reason that the message would be broken into individual parts and transmitted on all those frequencies, but on only one freq it looks like noise. Their arrays would all be in space and cover up to the lower gamma ray with planet size transmit/receivers. This would conceal any message in noise until a civilization was advanced enough to receive throughout the entire electromagnetic spectrum from large antennas in space. The X-ray/Gamma ray may be where the decoder ring exist and may give info on timing variations which would also keep unsophisticated creatures from cracking the code. The full electromagnetic spectrum would be like child’s play to a race even a thousand years ahead of us…
Apart from the speculative physics of creating all this spectrum, there is the issue of information density. Gamma-ray frequencies carry a lot more bits per unit time than longwave radio. So I don’t see the value of doing spread spectrum communication across such a wide range of frequencies.
Having said that, I agree with your main point about our rather parochial ideas on alien motives and technology. I suspect ETs are likely as different from us in ideas and technology as we are from stone-age humans, possibly even more so (the analogy of the ant colony next to a building site comes to mind). If ETCs are rare, then they are probably ahead of us by millions of years, assuming they can survive that long.
Why make it easy when they can make it terribly hard? Think of radio ham operators in the 1920s and 1930s picking up common communications from today that is encoded in so many different ways. What do you think about picking up something from a thousand years in our future… It makes sense to use as many ways as possible since they do not want others to learn their secrets or where their alien Swiss bank accounts are hidden. ;-}
It’s tangential to your comment, but possibly few cultures (if they exist at all) bother with large-scale interstellar flight. Once they get to the point where it’s a technically reasonable option, their own stellar systems out to their analogs of the Oort Cloud are so accessible that interstellar travel is mostly unnecessary. They can build (as you say) huge spatial instrument arrays for scientific study and communication, transport material across interplanetary distances with ease, collect all the energy they need from their own star. Maybe interstellar flight is attempted only for limited exploration or as a technological stunt. One more explanation for the Fermi Paradox…
NS, you fail to see our limited understanding when you believe in the Fermi Paradox. Fermi was a atomic physicist that was use to hands on experience since building the first atomic pile. The statement made in 1950 was one year after the Russians had exploded their first atomic bomb which was five years ahead of when it was expected. We forget how the world was in those days and should realize that Fermi expect exterrestrial civilizations would want to talk first to geniuses like him. The actual picture is UFOs where watching closely the development of nuclear weapons especial in the destructive explosions in the pacific. These were extremely dirty bombs and both in the pacific and San Francisco where the ships that were irritated where taken too and dismantled leaving to this day radioactive dust. So all that irritated atomic dust was sweeped under the rug but by 1950 the great atomic scientist where becoming aware someone else was watching these explosions besides the Russians.
Let me fill you in on what actually happened, Boron has been found in Angel Hair that was released in the 1950s from UFOs and at UFO landing sites. Boron is used in the safest fusion reaction p-11B fusion and Boron is used for Radiation shielding because it absorbs neutrons. Not only that but Avalanche energy is developing an Avalanche reactor design which is capable of fusing fuels like proton-boron-11 which practically eliminates internal neutron radiation, resulting in longer life and lower shielding. All this in the size of a lunch pail for the U.S. Air force and it works on a principle similar to magnetrons.
https://www.avalanche.energy/
We are not that far from interstellar flight and AI craft exploration of other stellar systems, so do you think that governments and scientist that may have killed 700,000 people are telling us the whole truth or the old fairy tail about the Fermi Paradox?
Nuclear Bomb Tests In The 1950s May Have Killed Almost 700,000 People, New Study Concludes.
https://wonderfulengineering.com/bomb-tests-1950s-may-killed-almost-700000-people/
Some interesting information from Wikipedia about Boron 10 and 11.
In nuclear reactors, 10B is used for reactivity control and in emergency shutdown systems. It can serve either function in the form of borosilicate control rods or as boric acid. In pressurized water reactors, 10B boric acid is added to the reactor coolant when the plant is shut down for refueling. It is then slowly filtered out over many months as fissile material is used up and the fuel becomes less reactive.
In future crewed interplanetary spacecraft, 10B has a theoretical role as structural material (as boron fibers or BN nanotube material) which would also serve a special role in the radiation shield. One of the difficulties in dealing with cosmic rays, which are mostly high energy protons, is that some secondary radiation from interaction of cosmic rays and spacecraft materials is high energy spallation neutrons. Such neutrons can be moderated by materials high in light elements, such as polyethylene, but the moderated neutrons continue to be a radiation hazard unless actively absorbed in the shielding. Among light elements that absorb thermal neutrons, 6Li and 10B appear as potential spacecraft structural materials which serve both for mechanical reinforcement and radiation protection.
Depleted boron (boron-11)
Radiation-hardened semiconductors.
Cosmic radiation will produce secondary neutrons if it hits spacecraft structures. Those neutrons will be captured in 10B, if it is present in the spacecraft’s semiconductors, producing a gamma ray, an alpha particle, and a lithium ion. Those resultant decay products may then irradiate nearby semiconductor “chip” structures, causing data loss (bit flipping, or single event upset). In radiation-hardened semiconductor designs, one countermeasure is to use depleted boron, which is greatly enriched in 11B and contains almost no 10B. This is useful because 11B is largely immune to radiation damage. Depleted boron is a byproduct of the nuclear industry (see above).
Proton-boron fusion
Main article: Proton-boron fusion
11B is also a candidate as a fuel for aneutronic fusion. When struck by a proton with energy of about 500 keV, it produces three alpha particles and 8.7 MeV of energy. Most other fusion reactions involving hydrogen and helium produce penetrating neutron radiation, which weakens reactor structures and induces long-term radioactivity, thereby endangering operating personnel. However, the alpha particles from 11B fusion can be turned directly into electric power, and all radiation stops as soon as the reactor is turned off.
https://en.wikipedia.org/wiki/Boron
Two interesting points:
The Voyager 1 spacecraft is having problems that may be related to how much Boron was used in the radiation-hardened semiconductors.
One of the more unusual practices that have been observed any number of times by aliens outside their landed spacecraft is fixing panels on the outside of it. Could they have been trying to tell us something about these panels being crucial to protecting them and the vehicle from radiation in space? ;-}
If only aliens had acted like John Carpenter in the movie The Day the Earth Stood Still we wouldn’t have had years of nuclear bomb testing and we would know that ETCs were out there. Of course, since we didn’t stop, Klaatu would have destroyed Earth…
Then we managed to make our missiles powerful enough to lob humans into orbit and even land on the Moon. So we know the scenario depicted in Earth vs the Flying Saucers is not the case either.
Those UFO aliens are tricky. No matter how much our technology changes, better cameras, still and video cameras in our pockets, they always manage to evade most of humanity, fuzz up the images to stay somewhat blurry, and do incomprehensible things like making crop circles, goring cattle, and experimenting on humans, and yet never allow a single piece of alien equipment or material get left behind as physical evidence. Not one alien got careless, and not one experimentee had the guile of a teenager to steal something before being released to tell their story. Even the crew of the Enterprise make those mistakes on occasion, as do real-life crews leaving tools and parts behind in aircraft and spacecraft. Yes, really tricky, as they have left us confused about their existence for at least three-quarters of a century
As for Fermi’s fellow scientists having opinions about all those bombs, Oppenheimer wasn’t too happy, to say the least.
IMO. the Fermi question remains an astute observation and deserves consideration.
Alex, I believe you are brilliant and not as a put down but you follow in Fermi footsteps. I present hard core data of what has been analyzed at UFO sites and you bring up the giggle factor of movies. You know what I have seen and what I take to be real scientific studies of UFOs not the comic book meetings that the head of the DOD senate UAP meetings referred to. Why do you think one of our representatives brought up the well known fact of UFOs disarming ICBMs. Why so many UAPs are seen to be seen near nuclear reactor and other nuclear sites. I’m not arguing that people see UFOs every day, all they need is a good pair of 10×50 binoculars to see that it is just a balloon or some other easily identified object. I do think the majority of real UFO close encounters are for our benefit by benign civilizations.
You will recall that you claimed that the new UAO investigation would reveal that they were real. So we had the first press conference and it was a…big nothing burger. Since the supposed “juicy” observations were then discussed behind closed doors, I have little doubt that new conspiracy theories about government coverups ignited. This feels like “wash, rinse, repeat” to me.
As I keep repeating, no advance in our technology and the availability of recording devices seems to unambiguously capture a genuine alien spacecraft. Only the hoaxes look impressive. The real recordings are always ambiguous and remain “unidentified”.
It is also worth reading @Brian Altmeyer’s May 26th comment on visitation frequency (an opinion I concur with, but with a caveat) that would seem to be incompatible with the many supposed incidents of alien spacecraft in our skies. In the context of the OP, it would imply that there is an expanding ETC with a frontier approaching us, that we cannot detect, yet there are many survey flights over Earth in a large variety of vehicle configurations.
I’m waiting for physical evidence of an artifact that is proven to be of non-terrestrial manufacture. Then I will change my mind. A paper about such an artifact, published in a peer-reviewed journal, would be very important, (assuming such an article could be published).
https://pbs.twimg.com/media/FUCCv8EXwAc3mAi?format=jpg&name=900×900
By chance, looking out of my office window I snapped this image of a UAO outside in the sky. [I have highlighted where to look]. Taken with an iPhone SE around 8 am, PDT. the camera is 12-megapixels. Digital zoom is used.
Despite the camera resolution, the object is still fuzzy due to size or distance. As far as I could tell, it was stationary.
UAO Central Valley CA, 8am, 5/27/2022
Nice pic. Similar to the one I saw in 1968 that chased down, overtook, then hovered in front of a flight of 12 B52s returning to Anderson on Guam after their Indochina bombing run.
Except it wasn’t fuzzy when not spinning. Fuzziness appears when it spins. Don’t ask me why. We just watched. Broad daylight, just like your pic, but larger, diameter = to height of B52 fuselage. Now of course you think I hallucinate. Btw, planes were low enough to discern the twin engine nacelles on each pylon. In 1968 no one had drone tech that could do what that thing did, hypersonic speeds, no sonic boom, hovering by spinning.
Thank you Dimjo! This is the problem, many people have seen UFOs well enough to discern the difference between common objects. Many scientist and engineers have also seen them, but because of ridicule and the stigma first started by the U.S. DOD and Fermi clear back in WWII, they have not been reported. How would advance civilizations interreact with what amounts too warring naked apes? Humans live in a world like the naive loner male thinking we are it and nothing else is better then us but fail to see the obvious right over our heads. I dare Alex and the rest of the scientific community to spend a million dollars on 200 megapixel camera cell phones and put them in a network around the world to capture images pointing strait up of UFOs. With automated AI being able to filter out the birds, bats, hoaxes and the many other objects not of unusual nature. It would also be very easy to give a parallax of distance and movement with two such cameras in separate locations say of 50 or more feet. Hopefully the Galileo project will release an open source version of their AI powered system to image UFOs/UAPs.
Fishing in Extraterrestrial Seas.
https://avi-loeb.medium.com/fishing-in-extraterrestrial-seas-23b7329ff769
To give you an idea of how afraid people are of talking about their UFO experience, my wife was upset about openly talking about this subject even though both of us have observed UFOs through our telescope. The stigma of being bullied and implied to being mentally ill because you see something that cannot be explained away is worse then being gay for many people. I have been lucky because in working for the U.S. Air Force and the FAA the workforce was well aware that UFOs are real and they have helped me learn about the systems that detect them…
>
The Hill
NATIONAL SECURITY
It is now irresponsible not to talk about UFOs.
05/28/22 12:00 PM ET
https://thehill.com/opinion/national-security/3503090-it-is-now-irresponsible-not-to-talk-about-ufos/
Well you need to buy the 200 megapixel cell phone camera from Samsung next year and a good tripod! https://petapixel.com/2022/05/27/samsung-shoots-building-size-photo-with-its-200mp-smartphone-camera/. As for the DOD does not know what the left hand and right hands are doing and do not expect anything out of them till 2050 on UAPs. As for high resolution images of UAPs in the next 2 to 3 years…
Won’t work.
None of these modern megapixel phone cameras have exposure speeds high enough to eliminate blur. All you would get is a room sized photograph with a blurred subject.
In 1968 all we had was 400 ASA film, with a 400mm telephoto. Can’t get a clear hand held telephoto image of a plane in flight. Even on a tripod, 400 ASA wasn’t fast enough to “freeze” a low flying jet.
I am amused when people claim that we should have a “clear” photo of a UFO given proliferation of cell phones.
It’s the duration of exposure, (shorter the better) not the pixels if you want a “clear” photo of a spinning object.
If you ever see a “clear” pic of a UFO taken with a cell phone, rest assured it’s a fake
For it to work:
All cell phones on the planet need:
1. A sensor so sensitive that the shutter speed in bright daylight automatically sets at 1/12000sec.
2. A setting on the phone that optimizes backlit photography against a blue sky or clouds, ignoring the preset settings that give us “nature/landscape” pics.
So, all cell phones on the planet would have settings for portraits, selfies, landscape, night and ‘UFO mode’ or bird mode or plane mode if ‘UFO mode’ is too giggly. (Even if a sensor is made that can take a picture in the dark, it will give a blurred UFO pic unless exposure speed is short.)
It takes about 1/8000sec to freeze the tips of a hummingbird wing in bright daylight. Not too many frozen pictures of the tips of a plane’s propeller, etc.
Then high megapixel count will allow us to enlarge the image.
We really do not need these shutter speeds. A hummingbird’s wingbeats do not in any way blur the rest of the bird. Similarly, we don’t need to see the propellers or turbine blades stilled in order to capture the image of an aircraft.
Movies are shot with 24 fps and one can see aircraft in flight in any movie you care to name. I just rewatched “The Court-Martial of Billy Mitchell” which ends with some 1950’s era swept-wing jet fighters flying overhead and they were perfectly recognizable as jet aircraft.
Even if UFOs were spinning madly and dashing about, we really only need to identify the vast majority of sightings as known objects. Birds, aircraft, weather balloons, planets, etc. Any real alien ships will be vanishingly rare by comparison, assuming they exist.
50x binoculars are very useful in discerning the nature of distant objects. That sort of optical zoom, coupled with a pixel density as great as the resolving power of our eyes would be quite adequate to clarify the images that are currently fuzzy. Video capture is even better, as multiple frames can be interpolated to tease out the detail that is lost at the pixel level.
Bottom line, I do not think that we need cameras with such fast shutter speeds as you suggest to capture good images of currently UAOs.
Thanks for the info, my expertize is with planetary lucy imaging which requires relatively small 1 to 10 megapixel special cameras that capture at 150 or more movie frames a second. These frames in the 10,000’s are then stack to correct for the atmospheric distortions.
AN INTRODUCTION TO LUCKY IMAGING FOR ASTROPHOTOGRAPHY.
https://skyandtelescope.org/astronomy-blogs/imaging-foundations-richard-wright/lucky-imaging/
What is new is the 200MP can take 120 frames a second by 4 way binning at 12.5MP which gives dim objects high detail and contrast. Not so much from cell phone but the actual HP1 chip is what is needed.
“The company says that photos taken at maximum size have an effective resolution of 16,384 x 12,288 pixels and can be captured at a rate of up to 7.5 per second. At a compressed 50-megapixel resolution, the sensor can shoot up to 30 frames per second, and up to 120 frames per second at 12.5-megapixels.”
This is the same with planetary imaging and what could be used is this chip to capture the object at full resolution then zoom in to the 12.5MP on the object as it crosses the field of the full chip. Another words use the chip as the locater then enlarge the image for high speed capture.
So I need to come clean on the image.
1. To my horror I realized I put the red circle around the wrong object. It should be around the larger fuzzy blob to the right.
2. The image falsifies my own idea of camera resolution. [I thought 10-megapixel cameras were a professional standard less than a decade ago. perhaps I am mistaken.] The iPhone SE only has digital zoom, rather than optical zoom, so all the zooming does is throw away the extraneous view, but doesn’t put more pixels on the image itself.
@Michael – maybe 200-megapixels would do it, although optical zoom would be just as good. I have mounted an older iPhone on a small refracting telescope to take images and video of birds on a feeder with fairly good results, although nowhere near professional quality.
3. Invisible on the image, but quite visible to the naked eye there are power lines running across the image. [Yes, we here in non-urban California still have those unsightly and dangerous powerlines on poles.]
Birds often sit on those powerlines.
4. The UAO was in fact, an identifiable object – a crow sitting on the powerline. Shortly after I took the image, it flew away and might have been more identifiable if I had captured a video instead.
My point, however, is that this sort of fuzzy image is going to be common, whether it is of UAOs, or the Loch Ness monster. It is just too easy to “see” something one expects to see, rather than what the object is. Image and video capture are still not great, at least in the hands of the general public. [Just look at the film camera quality from WWII from fighter plane kills, or the current ground object resolution using Google satellite images. ]
Taken together, the increased number of cameras should increase the number of UAOs observed, but the increased resolution should allow more positive identification, reducing the numbers. The result will always be a stream of fuzzy objects that cannot be identified because they are at the limits of identification.
It doesn’t matter if these records are from ubiquitous cameras in our pockets, military cameras in aircraft, radar tracks, or any other device able to record something at a distance. Given how good CGI is today, we should all be aware of how easy it is to fake images and videos. [Just look at how good is the latest Attenborough series “Prehistoric Planet” at depicting dinosaurs and ancient reptiles (although I am a bit suspicious of how pterosaurs are shown taking off in flight).]
Given how much we use spectrographic data to analyze objects, it seems a pity that we cannot deploy such devices on UAOs as this might give us more clues about the object than just the visual or IR recording, especially as inexpensive consumer devices are now available. AI coupled to such a device should be on the near horizon of technology available to consumers.
Nuclear weapons tests and the dangers of the Runit Dome.
MAY 30, 2022 2:04 PM PHT
‘The nuclear tests left the northern Enewetak islands more radioactive than Chernobyl or Fukushima’
https://www.rappler.com/voices/thought-leaders/opinion-nuclear-weapons-tests-dangers-runit-dome/
The Cold War’s nuclear weapons tests, and the damage and waste they left behind.
https://www.rappler.com/voices/thought-leaders/opinion-cold-war-nuclear-weapons-tests-damage-waste-left-behind/
I am always quick to defend negative results produced by SETI. I think I let my animosity towards the the variety principle and the universality dilemna distract me from a great paper. As a final poke though at the two ideas. Each creates a motivated people, the “not like the others” and ‘the immune to that filter”.
Would be interesting to see the model incorporate an expansion rate for colonization and exploration for each grabby civilization. We should also expect non-grabbies to engage in exploration. While the expansion rate for colonization would be optimized for biology and sensibilities, exploration would be optimized for physics. Exploration could progress much faster, creating inevitable one-way contacts. For the grabby civilization dogma this is important. How would a people dedicated to expanding react to the discovery of other peoples? One-way contact could be used as another driver turning the grabby dogma on or off.
As the area colonized expands, the distance from the center to the border of the territory increases. The cost to move value, even just information, between the center and the border increases. The difference in cost to express the grabby dogma for interior and boundary systems would always grow. Depending on technology and the laws of physics, interior systems are eventually unable to express the grabby dogma or receive less, possibly none, value from the dogma. The connection between distance and cost exists whether the dogma resides with a central authority or is distributed among all systems.
A grabby civilization could not achieve exclusive densities, colonization densities that preclude the emergence of other peoples emerging in their territory, unless they settle every system or make unwanted systems uninhabitable. Can grabby biology achieve this level of expertise without unlocking the knowledge of genetics and computation? More importantly, without using the knowledge? An ideal target world could be rendered uninhabitable by something as basic as chirality. Is this world skipped, destroyed, or adapted to? Space habitats may appear to be safe spaces where biology does not have to adapt. However, I think such habitats are more likely to be petri dishes for evolution and the integration of technology with biology.
Stick a big brain in a self replicating probe and you have the juvenile stage of a K1 or K2 person. Any species willing to go this route will expand faster than one that doesn’t.
This whole idea about intelligent life being inevitable and numerous out there comes from watching too many sci fi movies. This whole argument seems to be to explain why something we see on TV isn’t real. The lack of evidence for interstellar hopping aliens that Fermi mentioned seems pretty strong suggestion that they don’t exist. How uncommon is bacterial life itself? Unless there is panspermia with this much falling on every temperate terrestrial planet it may well be one to the negative 19th or some such odds of molecular life itself beginning not to mention all the probabilities of every step of additional complexity. Who even say intelligent creatures invent industrial technology or are able to maintain it? With non replacement birthrates and dysgenic political philosophies the norm in the developed world today who says in 600 years we aren’t back to living like the Amish with candles and horses again looking up at the ruins of cities that “must have been built by the gods.” Then the whole problem of flying spaceships to the stars is as challenging as an engineering project gets, and would require funding that would probably bankrupt the world. Nope, I bet when we get the answer we will find out we are alone in this galaxy and all the Seti talk will in retrospect look like wishful thinking.
“I bet when we get the answer”
How will you get that answer? What is the process you believe will determine that intelligent life exists nowhere in the universe except here?
Space is big, really big.
As Ron S. says below, how will we know we are alone. We cannot prove a negative, only that the weight of observations suggesting absence continues to reduce the probability.
It may be just your phrasing, but there is a hint that you believe Bethe’s “irreducible complexity” argument for the evolution of life and that “therefore” a deity created life, de novo.
Taken together, it could be implied that you think a deity created the Earth and life here, but nowhere else, putting us in a unique place in the universe, not just with civilization, but also with a living world, with the rest of the universe being sterile.
Wow. If you can pull all that from Savoy’s comment, would you be up for trying some remote viewing to find the aliens? :)
While we’re at it, I should say religious creationism shouldn’t be dismissed out of hand. It’s close enough to the strong anthropic principle for government work, and the latter is somewhat respected as rational in scientific circles. We live in a universe with sentient life because we couldn’t perceive any other. We live in a universe with rare sentient life because sentience is still absurdly unlikely even in the universes where it can happen. So we live on the one planet with consciousness, which is a very rare Earth indeed. That means nearly every detail of how this planet developed is the way it is because only that way could there be consciousness on it. It was, in effect, planned, and it was planned by force of consciousness. This consciousness is also the only reason why *anything* exists, because otherwise, who would perceive it? That makes the phenomenon of consciousness the Creator, and therefore every detail of this planet’s development was planned by the Creator. Q. E. D.
I’ve written this on this site previously, and would like to repeat that an ETC that was interested in advertising existence could easily construct a lighthouse using sunshades around a nearby star. Primitive monkey critters of earth are seriously discussing putting shades up to shield solar output in the name of climate change, so the general approach is probably known to any ET with better tech than humans.
The lighthouse would only need to be clearly artificial and aimed at the galactic plane. This is simple and obvious. No need to posit esoteric gamma ray tachyon spin star trek comms technology. Even ET would keep it simple. No reason to be complicated.
There aren’t lighthouses that I have heard of yet but these seem more plausible than much else. Unless of course time on instrument funding is the actual goal. If so, oops, my bad.
This is a good point. Still, I’m not sure the aliens will do this specifically to communicate — I’d expect that first they build starshades for climate control and power generation. By the time they have planetary-scale or larger engineering capacity to spare on METI without a message, they’ll probably assume anybody looking has noticed something is hinky in their system. Nonetheless, if somebody spots a warm Jupiter by transits, but RV doesn’t confirm it and the far side transits give unexpected results, they shouldn’t be saying “Darn!”; they should be saying “Hmmm….” :)
I read the paper and listened to some accompanying podcasts. It reminds me of an economics paper, and since Hanson is an economist it’s not so surprising.
The deductive logic rests on a few assumptions which may or may not be true: first, that life is equally likely to arise on all kinds of stars, which implies humans are early; then, that if aliens were grabby they would also be “loud”, and third, that there are no grabvy aliens in our past light cone. If all of those are true, then grabby aliens must be filling the universe st a high speed right now, and we just happen to not be near by.
I think this is really interesting and provides a lot of avenues for future research. Personally, I think the first assumption is dubious. Maybe we will learn yellow G stars are the only kind that can produce life like us. The second assumption may also be faulty. Could there be grabby aliens that we simply can’t detect? It seems possible — maybe they don’t build Dyson spheres but they do build surface colonies and we simply can’t detect them. The third assumption may also be false: we may be observing them right now but have misinterpreted them as natural astrophysics phenomena (like what are odd radio circles? How about fast radio bursts?) or we may have been “colonized” in the distant past many times over and the evidence of those long dead colonizers is now gone.
I should elaborate what I meant when I suggested the answer lies outside the EM spectrum. It seems like there are many ideas, though the aliens surely have better ones.
1: after the stars burn out and the fastest clocks tick in billions of years, neutrinos will gradually come to rest against each other in little clumps called “neutrino nuggets”. So far as I could tell, there’s some interesting new neutrino chemistry in those nuggets that may predominate petayears from now. But let’s not wait. The aliens could come up with advanced techniques to interact with neutrinos more effectively, make a neutrino megamolecule, something conceptually similar to DNA, which contains the text of an entire library. Send out a few tons of these tomes, each weighing about as much as a proton – let them soar through planets and stars with the greatest of ease, until somebody who knows how to scan for and stop neutrinos brings it to rest and puts it into a reader to get the data out.
2: Recently it was published that black holes have “quantum hair” that allow the information from infalling particles to escape, solving the black hole information paradox. I never did dig into that effectively, but if there is some kind of quantum gravity based signal that escapes a black hole, which is different from the standard general relativity gravity waves that would have been written about a hundred years ago, then maybe that’s a winning mode of communication.
3: dark matter. What is it? It whizzes all around the galaxies, seeming not to have many (any?) solid lumps that would wreak gravitational havoc with passing space stations. So is it a mindless hot gas, or is it a collection of data, or spaceships, or people, formed out of non Standard Model particles that contains all of the really *interesting* information in the universe?
4: high order photon structures. There has been much work with the orbital quantum number of light recently, skyrmions, photon-photon interactions. Is there a way to knot a group of photons together into a cosmic ray sized chunk of energy that contains an absurdly large amount of information and can be received, like the neutrinos, in an all or none way so that you don’t have to roll dice for every letter in the book you’re sent to see if you receive it?
Now you could pull out your Marconi set and say on a good day they can communicate with you in radio by tapping a key a mile away, but I don’t think they’re interested. It’s not just that it’s inefficient – it’s that they would have to go out of their way to intentionally first-contact a civilization that’s clearly not very advanced, with all the ethical calisthenics that might bring up, not to mention the worry that their willingness to prematurely first-contact us will be taken as assent for someone more advanced to prematurely first-contact them. They may well see an attempt to intervene in Earth’s political problems the way we would think about taking sides in a fight between two packs of wolves: a no-win situation that leaves them at risk of getting bitten. Or perhaps it’s more of an initiation (or hazing) rite, leaving humans to stew in absurdly shoddy philosophy the way an upperclassman might be amused to watch a freshman with a hangover. Whatever the reason, there is a chance we look back on all this together and laugh – discovering that much less was senselessly lost in our time by ourselves than we presently assume from the evidence of our senses.
So what you are saying is that while the SETI folks claim that all they have sampled is a glass of water from the Earth’s oceans looking for a fish, they are in fact taking glasses of liquid from the wrong ocean entirely.
Well, I don’t _know_ that. I’m not telling anybody to quit watching the skies. I don’t have anything here ready to submit to the patent office, let alone to start researching. There are lots more explanations for the Fermi paradox, some as obviously probable as they are dreadful. But — I hope the SETI researchers stay tuned for any new spectrum they are able to study.
Where did you read about neutrino nuggets and neutrino chemistry? I didn’t find much of anything.
Sorry I missed this before – I don’t know any way to keep up with these threads except by manually reading them. I think I encountered this all the way back in 2005 from Niayesh Afshordi’s work ( https://arxiv.org/pdf/astro-ph/0506663.pdf , which was published in Physical Review D). There are slides about it here ( http://cosmo05.uni-bonn.de/up/afshordi.pdf ). The idea seems to have persisted in some form to 2021 ( https://arxiv.org/pdf/2005.11889.pdf ) though it looks like this paper is about sterile neutrinos. I have gotten nowhere near an understanding of any of this, mind you. The idea appeals to a notion that the universe, when viewed in logarithmic time or something approximating that, can be considered to be in a relatively steady state, but with ever-changing rules of physics as the scales of distance and time increase in relation to the existing laws.
Sir Martin Rees supports the idea that any ETI we encounter will not be organic. In addition, any descendants who ply the stars may also become cybernetic in the process…
https://www.msn.com/en-us/news/technology/alien-life-may-have-already-been-replaced-by-robots-astronomer-claims/ar-AAYrx6q?rc=1&ocid=winp1taskbar&cvid=1d0850b970384f0a804c0b2883788e93
Well, China did say officially they would be using FAST to conduct SETI as part of their astronomical research with the now largest single radio telescope on Earth:
https://mp.weixin.qq.com/s/BtLLCb0GlPxjmhbAz5pUOw
https://www.iflscience.com/internet-is-aflutter-with-claims-of-alien-signals-detected-by-worlds-largest-telescope-64067
https://www.businessinsider.com/china-says-giant-telescope-maybe-found-signal-from-alien-civilization-2022-6
Even more unfortunate now that Arecibo is but a pile of scrap metal laying on the jungle floor of Puerto Rico. Then again, that institution publicly avoided SETI for most of its existence, and I say that as a known fact.
See here for just one example…
https://centauri-dreams.org/2009/11/18/%e2%80%9crubisco-stars%e2%80%9d-and-the-riddle-of-life/
and here…
https://centauri-dreams.org/2009/11/19/rubisco-stars-part-ii/
Why we need a dedicated SETI effort on the lunar farside, or maybe on some NEO planetoid that can stay shielded from Earth – assuming the skeptics are correct about RFI and can show the exact sources first:
https://www.salon.com/2022/06/15/chinese-telescope-aliens/
To quote:
Despite splashing headlines, the news initially drew skepticism from many in the astronomy world.
“I saw the news, but the report is sketchy on important details,” Avi Loeb, the former chair of the astronomy department at Harvard University, told Salon via email. “It is difficult to assess whether the signal is terrestrial or extraterrestrial without knowing its detailed properties, including the suggested source star.”
Indeed, Loeb said, a technical report about the findings would give astronomers a better chance at finding the original source of such signals.
End Quote.
Remember this SETI event from 2016:
https://centauri-dreams.org/2016/08/27/an-interesting-seti-candidate-in-hercules/
They claimed the signals were from a terrestrial military satellite, but they never pinpointed or announced which one it was supposed to be. Everyone, including the media, seemed glad it wasn’t an actual ETI signal and dropped the whole story.
This is not how science works. It is also an example of how and why we are taking so darn long to find alien intelligences despite claims to the contrary. The very idea of aliens scares a lot of people, including many scientists who want nice neat answers kept in their place, and religious folks who want the whole Universe to be just about us.
“This is not how science works.”
But it is how China works.
All too true.
As I said about the 2016 event from Russia, they too claimed it was signals from an errant military satellite, but they never identified which one and everyone subsequently dropped the subject.
Now everyone is saying it is RFI in regards to the Chinese report, yet no one has yet to identify which terrestrial sources are causing this, if any. As this new news item shows…
https://interestingengineering.com/china-fast-telescope-alien-life-humans
“Likely picked up human interference”, they say. Well, what interference? Where? Why? How hard is it to determine this? Why is everyone (but me apparently) seemingly satisfied with this answer?
It is not just the Chinese or Russians in this case who seem to be dropping the ball here.
http://astrobiology.com/2022/06/could-the-wow-signal-have-originated-from-a-stochastic-repeating-beacon.html
Could The “Wow” Signal Have Originated From A Stochastic Repeating Beacon?
Source: astro-ph.IM
Posted June 20, 2022 9:58 PM
The famous “Wow” signal detected in 1977 remains arguably the most compelling SETI signal ever found. The original Big Ear data requires that the signal turned on/off over the span of ~3 minutes (time difference between the dual antennae), yet persisted for 72 seconds (duration of a single beam sweep).
Combined with the substantial and negative follow-up efforts, these observations limit the allowed range of signal repeat schedules, to the extent that one might question the credibility of the signal itself. Previous work has largely excluded the hypothesis of a strictly periodic repeating source, for periods shorter than 40 hours. However, a non-periodic, stochastic repeater remains largely unexplored.
Here, we employ a likelihood emulator using the Big Ear observing logs to infer the probable signal properties under this hypothesis. We find that the maximum a-posteriori solution has a likelihood of 32.3%, highly compatible with the Big Ear data, with a broad 2 ? credible interval of signal duration 72 secs < T < 77 mins and mean repeat rate 0.043 1/days < ? < 59.8 1/days. We extend our analysis to include 192 hours of subsequent observations from META, Hobart and ATA, which drops the peak likelihood to 1.78%, and thus in tension with the available data at the 2.4 ? level.
Accordingly, the Wow signal cannot be excluded as a stochastic repeater with available data, and we estimate that 62 days of accumulated additional observations would be necessary to surpass 3 ? confidence.
David Kipping, Robert Gray
Comments: Re-submitted to MNRAS after first review
Subjects: Instrumentation and Methods for Astrophysics (astro-ph.IM); Popular Physics (physics.pop-ph)
Cite as: arXiv:2206.08374 [astro-ph.IM] (or arXiv:2206.08374v1 [astro-ph.IM] for this version)
https://doi.org/10.48550/arXiv.2206.08374
Submission history
From: David Kipping
[v1] Thu, 16 Jun 2022 16:55:45 UTC (2,816 KB)
https://arxiv.org/abs/2206.08374
Astrobiology, SETI
Checking in our neighbors – is anyone home?
Jun 2, 2022
The Allen Telescope Array has embarked on a survey of nearby stars
https://www.seti.org/checking-our-neighbors-anyone-home
The Secrets Behind The Alien Language In Arrival
Christian Gainey – June 21, 2022 at 9:15 PM
https://www.msn.com/en-us/movies/news/the-secrets-behind-the-alien-language-in-arrival/ar-AAYILPF
Chinese Astronomers Detect an Interesting (Probably not Alien) Signal With the FAST Radio Observatory
By Matt Williams, June 22, 2022
The 500-Meter Aperture Spherical Telescope (FAST), (aka. Tianyan, “Eye of Heaven”), is the largest radio observatory in the world. Since the observatory became operational in January 2020, this facility has made significant contributions to radio astronomy and the Search for Extraterrestrial Intelligence (SETI). In particular, the observatory has been instrumental in detecting Fast Radio Bursts (FRBs) and other cosmic phenomena that could be (but probably aren’t) possible indications of extraterrestrial communications.
Last week, while sifting through FAST data, the China Extraterrestrial Civilization Research Group (CECRG) from Beijing Normal University revealed that they discovered several signals that might be artificial in origin (a possible indication of an advanced civilization). These signals consisted of narrow-band electromagnetic radio transmission and were considered one of the best candidates for an extraterrestrial signal. Ah, but there’s a snag. According to subsequent news releases, those radio transmissions were apparently from Earth! [But no actual evidence yet, just assumptions.]
Full article here:
https://www.universetoday.com/156355/chinese-astronomers-detect-an-interesting-probably-not-alien-signal-with-the-fast-radio-observatory/
To quote:
“Berkeley’s SETI Research Center, Dan Werthimer, who is part of the international collaboration and was involved in the survey, denied this a few days later. “The signals that we found so far are all [radio frequency] interference,” he said. “They’re not from extraterrestrials. They’re from terrestrials.”
“Werthimer has reportedly co-authored a preprint paper that details how the FAST findings were a false positive. Ironically, Prof. Zhang was correct when he suggested this but was incorrect when he said it might take a long time to confirm or deny it.”
I just checked ArXiv: No such paper from Werthimer yet, but I did find this interesting one that he co-authored:
https://arxiv.org/abs/2003.09639
[Submitted on 21 Mar 2020 (v1), last revised 24 Mar 2020 (this version, v2)]
Opportunities to Search for Extra-Terrestrial Intelligence with the Five-hundred-meter Aperture Spherical radio Telescope
Di Li, Vishal Gajjar, Pei Wang, Andrew Siemion, Zhisong Zhang, Haiyan Zhang, Youling Yue, Yan Zhu, Chengjin Jin, Shiyu Li, Sabrina Berger, Bryan Brzycki, Jeff Cobb, Steve Croft, Daniel Czech, David DeBoer, Julia DeMarines, Jamie Drew, J. Emilio Enriquez, Nectaria Gizani, Eric J. Korpela, Howard Isaacson, Matthew Lebofsky, Brian Lacki, David H. E. MacMahon, Morgan Nanez, Chenhui Niu, Xin Pei, Danny C. Price, Dan Werthimer, Pete Worden, Yunfan Gerry Zhang, Tong-Jie Zhang, FAST Collaboration
The discovery of ubiquitous habitable extrasolar planets, combined with revolutionary advances in instrumentation and observational capabilities, has ushered in a renaissance in the search for extra-terrestrial intelligence (SETI). Large scale SETI activities are now underway at numerous international facilities. The Five-hundred-meter Aperture Spherical radio Telescope (FAST) is the largest single-aperture radio telescope in the world, well positioned to conduct sensitive searches for radio emission indicative of exo-intelligence. SETI is one of the five key science goals specified in the original FAST project plan. A collaboration with the Breakthrough Listen Initiative has been initiated in 2016 with a joint statement signed both by Dr. Jun Yan, the then director of the National Astronomical Observatories, Chinese Academy of Sciences (NAOC), and Dr. Peter Worden, the Chairman of the Breakthrough Prize Foundation. In this paper, we highlight some of the unique features of FAST that will allow for novel SETI observations. We identify and describe three different signal types indicative of a technological source, namely, narrow-band, wide-band artificially dispersed, and modulated signals. We here propose observations with FAST to achieve sensitivities never before explored.
Comments: 14 pages, 8 figures, Accepted by Research in Astron. Astrophys. (FAST special issue)
Subjects: Instrumentation and Methods for Astrophysics (astro-ph.IM)
Cite as: arXiv:2003.09639 [astro-ph.IM]
(or arXiv:2003.09639v2 [astro-ph.IM] for this version)
https://doi.org/10.48550/arXiv.2003.09639
Submission history
From: Di Li [view email]
[v1] Sat, 21 Mar 2020 12:00:19 UTC (3,684 KB)
[v2] Tue, 24 Mar 2020 06:49:23 UTC (3,679 KB)
https://arxiv.org/pdf/2003.09639.pdf
There is also this paper which has Dr. Werthimer’s name listed second among the authors/contributors:
https://arxiv.org/abs/2002.02130
[Submitted on 6 Feb 2020 (v1), last revised 25 Mar 2020 (this version, v2)]
First SETI Observations with China’s Five-hundred-meter Aperture Spherical radio Telescope (FAST)
Zhi-Song Zhang, Dan Werthimer, Tong-Jie Zhang, Jeff Cobb, Eric Korpela, David Anderson, Vishal Gajjar, Ryan Lee, Shi-Yu Li, Xin Pei, Xin-Xin Zhang, Shi-Jie Huang, Pei Wang, Yan Zhu, Ran Duan, Hai-Yan Zhang, Cheng-jin Jin, Li-Chun Zhu, Di Li
The Search for Extraterrestrial Intelligence (SETI) attempts to address the possibility of the presence of technological civilizations beyond the Earth. Benefiting from high sensitivity, large sky coverage, an innovative feed cabin for China’s Five-hundred-meter Aperture Spherical radio Telescope (FAST), we performed the SETI first observations with FAST’s newly commissioned 19-beam receiver; we report preliminary results in this paper. Using the data stream produced by the SERENDIP VI realtime multibeam SETI spectrometer installed at FAST, as well as its off-line data processing pipelines, we identify and remove four kinds of radio frequency interference(RFI): zone, broadband, multi-beam, and drifting, utilizing the Nebula SETI software pipeline combined with machine learning algorithms. After RFI mitigation, the Nebula pipeline identifies and ranks interesting narrow band candidate ET signals, scoring candidates by the number of times candidate signals have been seen at roughly the same sky position and same frequency, signal strength, proximity to a nearby star or object of interest, along with several other scoring criteria. We show four example candidates groups that demonstrate these RFI mitigation and candidate selection. This preliminary testing on FAST data helps to validate our SETI instrumentation techniques as well as our data processing pipeline.
Comments: 21 pages, 19 figures, 3 tables, published in ApJ
Subjects: Instrumentation and Methods for Astrophysics (astro-ph.IM)
Cite as: arXiv:2002.02130 [astro-ph.IM]
(or arXiv:2002.02130v2 [astro-ph.IM] for this version)
https://doi.org/10.48550/arXiv.2002.02130
Journal reference: The Astrophysical Journal, Volume 891, Issue 2, id.174(2020)
Related DOI:
https://doi.org/10.3847/1538-4357/ab7376
Submission history
From: Zhi-Song Zhang [view email]
[v1] Thu, 6 Feb 2020 07:09:58 UTC (9,593 KB)
[v2] Wed, 25 Mar 2020 09:05:53 UTC (5,068 KB)
https://arxiv.org/pdf/2002.02130.pdf
It is unfortunate that Arecibo was always so squeamish about SETI and METI (but what about SETI@Home, I hear the cry. Yes, what about it? Where is all that data they collected and how much has been properly analyzed?). I can only imagine how far we might be if they and the science community in general took searching for intelligent extraterrestrial beings more seriously and had real funding for it.
https://arxiv.org/abs/2206.09820
[Submitted on 20 Jun 2022]
Earth through the looking glass: how frequently are we detected by other civilisations through photometric microlensing?
S. Suphapolthaworn, S. Awiphan, T. Chatchadanoraset, E. Kerins, D. Specht, N. Nakharutai, S. Komonjinda, A.C. Robin
Microlensing is proving to be one of the best techniques to detect distant, low-mass planets around the most common stars in the Galaxy. In principle, Earth’s microlensing signal could offer the chance for other technological civilisations to find the Earth across Galactic distances.
We consider the photometric microlensing signal of Earth to other potential technological civilisations and dub the regions of our Galaxy from which Earth’s photometric microlensing signal is most readily observable as the “Earth Microlensing Zone” (EMZ).
The EMZ can be thought of as the microlensing analogue of the Earth Transit Zone (ETZ) from where observers see Earth transit the Sun. Just as for the ETZ, the EMZ could represent a game-theoretic Schelling point for targeted searches for extra-terrestrial intelligence (SETI). To compute the EMZ, we use the Gaia DR2 catalogue with magnitude G<20 to generate Earth microlensing probability and detection rate maps to other observers.
Whilst our Solar system is a multi-planet system, we show that Earth's photometric microlensing signature is almost always well approximated by a binary lens assumption. We then show that the Earth is in fact well-hidden to observers with technology comparable to our own.
Specifically, even if observers are located around every Gaia DR2 star with G<20, we expect photometric microlensing signatures from the Earth to be observable on average only tens per year by any of them. In addition, the EMZs overlap with the ETZ near the Galactic centre which could be the main areas for future SETI searches.
Comments: 15 pages, 12 figures, 3 tables
Subjects: Earth and Planetary Astrophysics (astro-ph.EP); Astrophysics of Galaxies (astro-ph.GA); Instrumentation and Methods for Astrophysics (astro-ph.IM)
Cite as: arXiv:2206.09820 [astro-ph.EP]
(or arXiv:2206.09820v1 [astro-ph.EP] for this version)
https://doi.org/10.48550/arXiv.2206.09820
Submission history
From: Suphakorn Suphapolthaworn [view email]
[v1] Mon, 20 Jun 2022 14:54:11 UTC (18,906 KB)
https://arxiv.org/pdf/2206.09820.pdf
Exoplanet imaging could be humanity’s best chance to find extraterrestrial intelligence
by Justinas Vainilavi?ius
06 July 2022
https://cybernews.com/editorial/exoplanet-imaging-could-be-humanitys-best-chance-to-find-extraterrestrial-intelligence/
http://astrobiology.com/2022/07/viability-of-quantum-communication-across-interstellar-distances.html
Viability Of Quantum Communication Across Interstellar Distances
Source: quant-ph
Posted July 10, 2022 at 9:46 PM
The possibility of achieving quantum communication using photons across interstellar distances is examined. For this, different factors are considered that could induce decoherence of photons, including the gravitational field of astrophysical bodies, the particle content in the interstellar medium, and the more local environment of the Solar System.
The X-ray region of the spectrum is identified as the prime candidate to establish a quantum communication channel, although the optical and microwave bands could also enable communication across large distances. Finally, we discuss what could be expected from a quantum signal emitted by an extraterrestrial civilization, as well as the challenges for the receiver end of the channel to identify and interpret such signals.
Arjun Berera, Jaime Calderón-Figueroa
Comments: 18 pages. In Press Physical Review D
Subjects: Quantum Physics (quant-ph); General Relativity and Quantum Cosmology (gr-qc); High Energy Physics – Phenomenology (hep-ph)
Cite as: arXiv:2205.11816 [quant-ph] (or arXiv:2205.11816v1 [quant-ph] for this version)
https://doi.org/10.48550/arXiv.2205.11816
Submission history
From: Jaime Calderón Figueroa
[v1] Tue, 24 May 2022 06:25:44 UTC (57 KB)
https://arxiv.org/abs/2205.11816
Astrobiology, SETI, Technosignature, Interstellar
https://arxiv.org/abs/2205.11816
https://arxiv.org/pdf/2205.11816.pdf
Snooping on Alien Messages Passing Through the Solar System
JULY 9, 2022
BY LAURENCE TOGNETTI
Researchers at Penn State University have studied a new technique that could use a star’s ability to focus and magnify communications which could be passing through our own solar system, and has been accepted for publication in The Astronomical Journal and was part of a graduate course at Penn State covering the Search for Extraterrestrial Intelligence (SETI. The study describes our Sun as potentially acting as a kind of node as part of an interstellar communication network involving probes or relays near our Sun, acting like cellular telephone towers in space.
Full article here:
https://www.universetoday.com/156658/snooping-on-alien-messages-passing-through-the-solar-system/
The paper online here:
https://arxiv.org/abs/2206.14807
To quote:
Unfortunately, the students did not detect any signals of extraterrestrial origin in the wavelengths they observed, and since this study was a class project, the research carried out only involved one night of observations. However, the insight into how we might contact extraterrestrial civilizations beyond Earth no doubt proved invaluable to both the faculty and students involved in the project. This particular graduate-level course is only one of two in the world, with the other at the University of California, Los Angeles, that encourages students to conduct such radio-based SETI projects and publish their results in a scientific journal.
“This graduate course is the centerpiece of the Penn State Center for Extraterrestrial Intelligence,” said Wright. “Students come from a variety of disciplines, including astrobiology, astronomy, chemistry, and geophysics. This year, because it was a hybrid class, we even had a student from another university join us. One of the neat things about this class is that, because the SETI field is so young, it is possible for students to make a real contribution and publish research. It’s remarkable.”
What would a Kardashev Type 3 civilization sound like…
Radio telescope picks up persistent signal from a galaxy far far away
Anugraha Sundaravelu
Wednesday 13 Jul 2022 4:06 pm
https://metro.co.uk/2022/07/13/radio-telescope-picks-up-radio-signals-from-a-far-away-galaxy-16994134/
To quote:
This signal consisted of a four-day window of random bursts that then repeated every 16 days. The new discovery was picked up by a telescope in British Columbia, Canada on 21 December 2019.
The telescope, which is part of the Canadian Hydrogen Intensity Mapping Experiment (CHIME) was being manned by Dr Daniele Michilli when the mysterious signal appeared.
‘It was unusual. Not only was it very long, lasting about three seconds, but there were periodic peaks that were remarkably precise, emitting every fraction of a second – boom, boom, boom – like a heartbeat,’ said Dr Michilli who thinks the flashes might be coming from a distant radio pulsar or magnetar.