I sometimes imagine Claudio Maccone having a particularly vivid dream, a bright star surrounded by a ring of fire that all but grazes its surface. And from this ring an image begins to form behind him, kilometers wide, dwarfing him and carrying in its pixels the view of a world no one has ever seen. The dream is half visual, half diagrammatic, but it’s all about curving Einsteinian spacetime, so that light flows along the gravity well to be bent into a focus that extends into linear infinity.

My slightly poetic vision of what happens beyond 550 AU or so doesn’t do justice to the intrinsic beauty of the mathematics, which Maccone learned to unlock decades ago as he explored the concept of an ‘Einstein ring’ as fine-tuned by Von Eshleman at Stanford. When I met him (at one of Ed Belbruno’s astrodynamics conferences at Princeton in 2006), we and Greg Matloff and wife C talked about lensing at breakfast one morning. Even then he was afire with the concept. He’d been probing it since the late 1980s, and had submitted a mission proposal to the European Space Agency. He had written a short text that would later be expanded into the seminal Deep Space Flight and Communications (Springer, 2009).
Maccone said in his presentation at the Interstellar Research Group’s Montreal symposium that he was delighted to see the Sun’s gravitational focus moving into the hands of the next generation, citing the 2020 NASA grant to Slava Turyshev’s team at JPL, where a Solar Gravitational Lens mission is being worked out at the highest level of detail as an entrant into the sweepstakes known as the Heliophysics 2024 Decadal Survey. To see how far the concept has gone, have a look at, for example, Self-Assembly: Reshaping Mission Design, or A Mission Architecture for the Solar Gravity Lens, among numerous entries I’ve written on the JPL work.

Image: A meter-class telescope with a coronagraph to block solar light, placed in the strong interference region of the solar gravitational lens (SGL), is capable of imaging an exoplanet at a distance of up to 30 parsecs with a few 10 km-scale resolution on its surface. The picture shows results of a simulation of the effects of the SGL on an Earth-like exoplanet image. Left: original RGB color image with (1024×1024) pixels; center: image blurred by the SGL, sampled at an SNR of ~103 per color channel, or overall SNR of 3×103; right: the result of image deconvolution. Credit: Turyshev et al., “Direct Multipixel Imaging and Spectroscopy of an Exoplanet with a Solar Gravity Lens Mission,” Final Report NASA Innovative Advanced Concepts Phase II.
The astounding magnification we could achieve by using bent starlight was what drew me instantly to the concept when I first learned about it – how else to actually see not just pixels from an exoplanet around its star, but actual continents, weather patterns, oceans and, who knows, even vegetation on the surface? But at Montreal, after his praise for the JPL effort that could become our first attempt to exploit the gravitational lens if adopted by the Decadal survey, Maccone took a much more futuristic look at what humans might do with lensing, delving into the realm of communications. What about building a radio ‘bridge’?
The concept is even more audacious that reaching 650 AU with the payloads we’ll need to deconvolve imagery from another star. In fact, it’s downright science fictional. Suppose we achieve the technologies needed to send humans to Alpha Centauri. We have there in the form of Centauri A a G-class star much like the Sun (although we could also use the K-class star Centauri B). Both of these stars have their own distance from which gravitational lensing occurs, Align your spacecraft properly to look back towards the Earth from Centauri A and you can now connect to the ‘relay’ at the lensing distance from the Sun. You’ve drastically changed the communications picture by using lensing in both directions.
The consequences for contact and data transfer are enormous. Consider: If we want to talk to our crew now orbiting Centauri A and try to do so with one of the Deep Space Network’s 70-meter dish antennae using today’s standards for spacecraft communications, we’d have no usable signal to work with. Assume a transmitting power of 40 W and communications over the Ka band (32 GHz) at a rate of 32 kbps (these are the figures for the highest frequency used by the Cassini mission). The distances are too great; the power too weak. But if we factor in a receiver at the lensing point of Centauri A directly opposite to the Sun, we get the extraordinary gain shown in the diagram below.
This raises the eyebrows. Bit Error Rate expresses the quality of the signal, being the number of erroneous bits received divided by the total number of bits transmitted. Using a spacecraft at the solar gravitational lens distance from the Sun talking to one on the other side of Centauri A (alignment, of course, is critical here), we have a signal so strong that we have to go over 9 light years out before it begins to degrade. A radio bridge like this would allow communications with a colony at Alpha Centauri using power levels and infrastructure we have in place today.
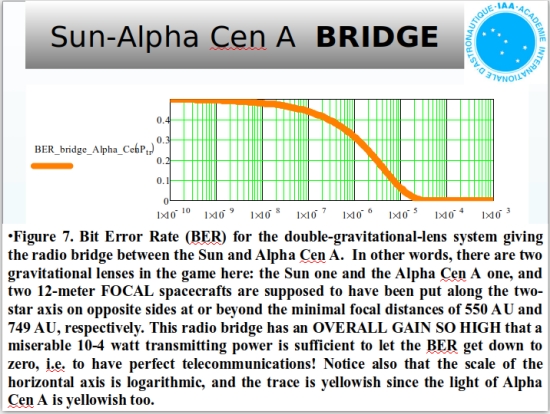
Obviously, this is a multi-generational idea given travel times to and from Alpha Centauri. But it’s a step we may well need to take if we can solve all the problems involved in getting human crews to another star. Maccone told the audience at Montreal that in terms of channel capacity (as defined by Shannon information theory), the Sun used as a gravitational lens allows 190 gigabits per second in a radio bridge to Centauri A as opposed to the paltry 15.3 kilobits per second available without lensing.
Realizing that any star creates this possibility, Maccone has lately been working on the question of how a starfaring society of the future might use radio bridges to plot out expansion into nearby stars. He is in fact thinking about the best ‘trail of expansion’ humans might use to keep links being built and used between colonies at these stars. This turns out to be no easy task: The first goal must be to convert the list of nearby stars being studied (the number is arbitrary) into Cartesian coordinates centered on each star (their coordinates are currently given in terms of Right Ascension and Declination with respect to the Sun). Maccone calls this an exercise in spherical trigonometry, and it’s a thorny one.
A network of radio bridges between stars could evolve into a kind of ‘galactic internet,’ a term Maccone uses with an ironic smile as it plays to the journalist’s need to write dramatic copy. Be that as it may, the SETI component is intriguing, given that older civilizations may even now be exploiting gravitational lensing. It would be an interesting thing indeed if we were to discover a bridge relay somewhere at our Sun’s gravitational lensing distance, for its placement would allow us to calculate where the receiving civilization must be located. Using a gravitational lens for communications is, after all, extraordinarily directional. Might we one day discover at the lensing distance from the Sun an artifact that can open access to a networked conversation on the interstellar scale?
Human expansion to nearby stars would likely be a matter of millennia, but given the age of the galaxy, it would represent just a sliver of time. Whether humanity can survive for far shorter timeframes is an immediate question, but I think it’s refreshing indeed to look beyond the current work on reaching the solar gravitational lens to the implications that would follow from exploiting it. The radio bridge is great science fiction material – we might even call it the stuff of dreams – but solidly rooted in physics if we can find the tools to make it happen.



That is broadband internet service. Higher than a number of ISPs can manage in the US, and far higher than available in many US rural areas. Pity we are stuck with the rather high latency. I imagine the communication would be 2-way streaming rather than on-demand.
I can just imagine the upset – “We can get broadband delivery to and from Alpha Cen, over 4 ly away, but not to my house outside city[X] in my state?”
Just not let it be managed by one of the big ISPs. ;-)
Given that the stars are always moving relative to each other, a narrow beam will inevitably need to be repositioned, with both transmitter and receiver moving around the sphere at a distance where the signal is best received and transmitted. Would the “backbones” of the “galactic internet” be between stars that are very stable wrt. each other to minimize the repositioning? Or, as I think was mentioned in another post, the use of black holes or even neutron stars to reduce the distance from the star to the SGl line? Another possibility is to have the equivalent of a Dyson swarm surrounding the star so that the repositioning is handled by switching the signal reception and [re]transmission to different comsats.
190 Gbps would allow for very short transients if simple messages like protocol handshakes were being sent.
Best is white dwarfs, close in SGL’s and plenty of power from the stars. If siruis b had a probe in orbit it could quickly change orbits using the two stars light and stellar winds. There are many WD’s around the solar neighbourhood as well so plenty of opportunities for comms.
Like many modern services, become more and more accustomed to thinking about them. Looking at the Sol based problem, had noticed that there were some drift problems due to the fact that the sun precesses driven by Jupiter and Saturn in circles of about a million kilometers. So that does cause targeting drift out at 550 AUs if you are fixed on another star or planet. With Alpha Centauri though, this gets a little more complicated, with a cycle of about 80 years of orbital motion about a center of mass with about 23 or so AUs average separation. In some ways this does not sound like much, but it could also be looked at like threading a needle.
But then the actual center of mass of a binary system is a lot more stable from a remote observer’s standpoint. And it is exposed out in space. I keep wondering if the GR properties associated with individual stars could be applied to barycenters. Here and there ( e.g. Pluto and Charon) they are not buried underneath overlying layers of baryonic matter.
A proposed test of General Relativity: place a GPS satellite at the Pluto Charon barycenter ( or adjusted for other satellites) and see what the time retardation is.
Poke at it. Maybe something serendipitous will result.
Use of a mass as a gravitational lens requires that it be effectively a point source of gravity at the distance where the Einstein ring forms. While any spherically symmetric mass would qualify, barycenters wouldn’t unless you were looking for an Einstein ring well outside the actual distribution of mass; The light isn’t attracted to the barycenter itself, it’s attracted to the various bodies, which only averages to being at the barycenter when you’re well outside the system as a whole.
The same reasoning would apply to any distribution of mass with a hole through the center. There’s no focusing effect inside a toroidal mass, for instance. For the same reason gravity declines to zero at the center of a spherical body.
So, yeah, if you had a tight multiple star system, from far enough away you’d get an Einstein ring around the system, but there could never be one *between* the stars.
The first step in a telescope 4ly wide…quite the interferometer
No matter how appealing a mission to the solar gravitational lens is for modern humans, on the cosmic scale it is just a crutch. The SGL sorts out light from different places to different spots in space, but all that light is passing by us anyway. When the number of desired vantages grows large enough, it should make more sense to spray out a networked swarm of detectors at least a few times the radius of the Sun. These should scan all EM frequencies, all the time, using quantum interferometry to extract all possible information to develop images in every possible direction — like our planet’s VLBI arrays, but with better transmission rate, electronics and deconvolution. I imagine graphene-like compounds might be a useful working material. They might look like cosmic dust. Can you imagine working out how to access an API for some the cosmic dust we see now, and all at once you can view all the archived astronomical records of the entire Universe?
But the detector swarm doesn’t solve the low-power transmission advantage of the solar gravity creating a parallel beam that in turn is focused at the target system to receive an extremely high bandwidth signal.
It seems to me that by defocusing the beam a little, the transmission can trade bandwidth for a less precise pointing transmission. If the receiving signal was just 19 kbps (like the olde modem dial-up system), the signal could be spread over an area with a radius 3000x larger. [This calculation may be wrong given that the receiver may not get the needed signal strength to avoid losses and not be able to get the focus needed for the fraction of the signal that can be collected at the SGL. I leave it to comms experts to correct this very crude estimate.]
The “interstellar internet” is a very nice theoretical means to send transmissions around the galaxy using lower power transmitters, bypassing the constraints applied to interstellar communication. It also implies that any “galactic club” could be extant, just not visible to use, as they are not using the technology we first envisaged back in the 1960s, but rather a more sophistical and elegant way of sending information throughout the galaxy, even to a galactic “empire” of a single civilization.
Even if the 190 Gbps bandwidth is too generous, it does imply a lot of data transmission that could be streamed across the stars. That is potentially a lot of simultaneous channels of different media sent in packets to specific destinations. The time delay between sending and receiving is potentially very great, although probably reasonable for nearby stars. It would certainly be sufficient as a tool to warn about predatory STL starships from a distant predator civilization.
I think this is a very interesting idea that I would like to see extended to determine how it could be achieved by an interstellar civilization[s], with solutions to ensure it remains robust (e.g. multiple routes, transmitter and receiving repositioning, protocols possibly extended from the Deep Space Network, etc.).
@Michael – I would like some pros and cons with numbers about using different stellar types as the nodes in the network. Where are the foci, orbital velocity to stay on a single SGL, requirement for multiple units around the same star to maintain a transmission, etc.
@Alex: I think a satellite swarm could achieve similar advantages on transmission, simply by broadcasting everything with the same phase relative to the target star. I’d compare the transmitter arrays on 5G cell phones, which can use “beamforming” to route signals through architectural obstacles without aiming any physical antenna. I think this paper addresses this application in orbit, though I don’t feel competent to compare the relative advantages of the two approaches: https://arxiv.org/pdf/2308.05055.pdf
“view all the archived astronomical records of the entire Universe?”
Reminds one of the lines:
Hold Infinity in the palm of your hand
And Eternity in an hour.
– William Blake
With such a low error rate we might even venture a transporter/teleport beam some day. Beam me out.
Let’s keep our “eyeballs peeled” for space rocks with a grid in their surface and/or an antenna. And avoid disturbing their orientation, trajectory and physical integrity.
Might the first of them contain the equivalent of two-way tickets to Stockholm?
Hi Paul
The distance to the Gravitational Lensing Zone (GLZ) is so large because the Sun is opaque to the EM radiation we use. But what if the Sun is transparent to the radiation involved? The Neutrino GLZ is much, much closer – somewhere out near Uranus’s radial distance.
How do you calculate this? I assu,e you mean the neutrino equivalent to the Einstein ring is inside the solar radius. But where? As the radius decreases, the gravitational force is also decreased linearly. Is there some optimum near the sun’s radius that maximizes the bending of the neutrinos?
Alex
https://www.sciencedirect.com/science/article/abs/pii/0375960188905713?via%3Dihub
IIUC, in the case of neutrinos passing through the sun, as g increases with radius, the whole of the sun’s volume acts as a convex lens to focus the rays about 3.5 bn km from the sun. So no Einstein ring.
What I am not clear about is that the sun emits neutrinos too, so is that local flux relatively unimportant at the distance of the focal point?
Now if only we had a neutrino detector that was small enough…
There’s a wonderful sci-fi novel – “Rose and Worm” by Robert Ibatullin – where a whole Galanet is built on gravitational lensing networks. It goes into much detail, i. e. what types of stars are the best for the nodes, how locals would react to discovery of routers, etc. Also, it gives a very credible and elaborate concept of structure and evolution of galactic society. And, finally, the plot itself is magnificent!
Gravity waves should also be concentrated, might be a good way to look at gravity waves from the big bang. Perhaps a large neutrino detector on one of Uranus’s moons.
Gravitational lens focusing power is inversely proportional to wavelength, which for typical GW sources is huge. There will be some focusing, but probably not enough to allow compact detectors even for high-frequency emissions.
Neutrinos are completely different matter, their wavelengths are comparable to gamma rays. And since Solar core is not convecting, there are less limitations to the focusing power. A direct look from Kuiper Belt into cores of stars and their remnants is completely possible.
It would allow us to perhaps use these SGL lines to observe neutron or pulsar stars with great accuracy allowing us to to have huge base lines to see gravity waves move through the universe. Even if we looked at stars across the universe their fleeting change in position could indicate a GW moving through spacetime. I have said before no matter where we point these scopes they will revel a wealth of information such is their power.
This is a very cool concept. Although news from Alpha Centauri A would still be 4.3 years late. Unless you’ve got warped time space or Stargates at the gravitational inflection point. Which would mean that you send radio signals as wave packets through or FTL warp packets.
How difficult would it be to identify as artificial such a low power signal smeared along an Einstein ring? Encryption and broadband transmission would make the signal even harder to identify. This network may be impossible to detect without an access key.
The gravitational lens only works with stars and exoplanets, because stars emit a huge amount of EMR in the visible light. Radio signals of low power would remain low power and would not increase in power by gravitational lens which is why we need a million watts of power just to send a signal to the nearest star. The gravitational lens only works on the large scale.
Hi Geoffrey
Actually the lensing works perfectly well for EM signals of any strength. That’s the whole point of Claudio Maccone’s work, which Paul has discussed here many times.
If I recall correctly, some or perhaps the early elaboration of gravitational lensing described the light sources as point sources. But another way of looking at this phenomenon is to consider light from a star or planet an expanding spherical wave front until it contacts the gravitational distortion of the sun or another star. If this is the case, it could be that the whole hemisphere of the sun is collecting photons from a star – and not just bending a point source image ( the local terrestrial effect).
If that is the case, and if it is highly efficient, then the whole Galaxy would be laced with very intense beams of energy slicing about the interstellar medium. A nearby star such as Alpha Centauri, though attenuated by distance, would be an example.
Whatever the efficiency of collection over a 700,000 km wide receiver, the rebroadcast would be very intense if beamed like a laser. And now and then something like that would rip through objects in the Oort Cloud. Hypothetical, but worth looking into.
Now the sun and Alpha Centauri would be just an ordinary example. If this model holds water, what would be going on surrounding a binary neutron star? Or in globular clusters? Or the galactic bulge? Would tend to heat up a lot of Cold Dark Matter, one would suspect. We might be able to gather data pro or con on this phenomenon with some conventional but “pointed” astronomical observation.
I am not sure about “intense beams”. The light does bend around the gravitational source which is why we see distant galaxies that appear brighter and often duplicated when a strong gravitational source is in front of the galaxy.
But the creation of parallel beams requires a source somewhere on the gravitational focal line. The farther away from the star, the greater the separation of the Einstein ring from the star, as g weakens. At some point it is too weak to produce a good focus on the focal line. For the majority of stars, even binaries, the separation of the stars is too great to create the light beam. It will occur for a minority of multiple star systems, although unless the eccentricity is low, any beam will turn on and off.
How many stars would meet the needed criterion of being inside the inner and outer edge of their focal lines? That would be an interesting statistic to determine. After that, what would be the probability of such a beam being intercepted by our system, and for how long? Is your idea a possible reason for the “Wow! signal”?
There should be intense beams of light from some favourable binary stars and distances between them. For example the magnification of sirius a by b would up to i think around 200 times at their nearest. Its the ratio between the distances between them and the focal distance of sirius b.
@wdk: Interesting notion! In a first search of Arxiv I didn’t find anything I could recognize as clearly relevant, but stumbled across an even odder situation: a system of three black holes in which the gravitational waves from two of them are lensed by a third further away. https://arxiv.org/abs/2209.06459 Alas, I understand virtually nothing of that paper. Maybe this could work in a sci-fi story as the explanation for a planet to abruptly have its orbit shifted or destabilized… though I bet this is a massive exaggeration.
Continuing on binary systems, lensing and GR, I’d like to submit the example the neutron- pulsar binary system. Some background:
Since m was initially discovered, the tightly bound neutron star and pulsar’s orbit has decreased in energy due to propagation of gravitational waves
described by Albert Einstein’s general theory of relativity.
The ratio of observed to predicted rate of orbital decay is calculated to
be 0.997 ± 0.002.[12] The total power of the gravitational waves
emitted by this system presently is calculated to be 7.35 × 10 to the 24th watts.
Below, follow some really accurate orbital parameters, from which has been
extracted the orbital decay rate which predicts an eventual merger.
Mass of neutron star companion: 1.387 M☉
Total mass of the system: 2.828378 M☉
Orbital period: 7.751938773864 hr
Eccentricity: 0.6171334
Semi-major axis: 1,950,100 km
Periastron separation: 46,600 km
Apastron separation: 3,153,600 km
Orbital velocity of stars at periastron (relative to center of mass): 450 km/s
Orbital velocity of stars at apastron (relative to center of mass): 110 km/s
In the Wikipedia article from which this was extracted, the Solar gravitational radiation induced by the planets was calculated as 5000 watts by comparison.
Now, since the pulsar and neutron stars are really distinguished mainly by one having a powerful magnetic field, and the other not, a simple question:
From where specifically in this system is all this gravitational radiation emanating?
If the magnetar and neutron stars orbits are decreasing towards the their barycenter, isn’t the source of the gravitational energy from the reduced potential gravitational energy of both stars wrt. the barycenter where the 2 stars will end up after merging?
However, as gravity is a curvature in spacetime, is it true to say that there is any “emission” at all? Just as ocean waves and electrical emh is not due to water (H2O) molecules or electrons moving with the wave or electrical current, is the energy of gravity waves not due to any emissions or losses of material from any of the stars (unlike the lost of Helium and photons emitted by the sun), but rather the loss of potential gravitational energy as the stars fall towards their barycenter?
https://en.wikipedia.org/wiki/Sticky_bead_argument
Although whether a rigid rod is sticky or not as it encounters the gravitational wave is likely a matter of scale – like the ‘great rip’ the gravitational stress on larger objects at sufficiently large scale would overcome molecular stresses, making the rod ‘elastic.’
@wdk: My understanding is limited, but look up gravitomagnetism. https://en.wikipedia.org/wiki/Gravitomagnetism for example; also look up the stress-energy tensor. Each planet and star emits no gravitational waves … when viewed from their own frame of reference. But from any other viewpoint, they tend to drag things a little in whatever direction they are going – not straight line gravity, but gravitomagnetism. (Since free fall, unlike a particle subject to electrical interaction, is always considered “rest”, this is called “frame dragging”) I suppose this isn’t a free source of energy because every other particle in the universe is simultaneously exerting gravitomagnetic effects the other way – you can’t wiggle the universe without it wiggling you back – slowing you down by action-reaction.
So I think if one star is moving at 1 km/s and another is at the moment orbiting past it at 2 km/s in the same direction, Earth (moving at the same speeds from their viewpoints) slows down the second star by gravitomagnetism a bit more than the first. The net decrease in the other star’s kinetic energy observed from either star in that system should match the yield of energy at Earth.
Interesting, will have to form some new neural connections to ponder: “Gravitomagnetic arguments also predict that a flexible or fluid toroidal mass undergoing minor axis rotational acceleration (accelerating “smoke ring” rotation) will tend to pull matter through the throat (a case of rotational frame dragging, acting through the throat). In theory, this configuration might be used for accelerating objects (through the throat) without such objects experiencing any g-forces.”
Wondering if this zero-g acceleration constitutes a space warp?
A. T.,
Two things here to which to respond.
1. Consider Alpha Centauri A or B as a point source of light in a telescope in a back yard, I guess, in the southern hemisphere. That 10 cm aperture telescope did not collect very much light. Now consider the proposition of Alpha Centauri flux spread out over four light years – but collected by the entire 1.4 million kilometer diameter of the sun. And then sent out in a focused beam on the other side of the sun. And then this going on all over the galaxy. If true, that’s quite a grid – and every once in a while it’s going to zap the crows that alight on the high tension wires, Or the debris in interstellar space. When we talk about dialing into that interstellar optics to get planetary images, there’s this other side of the coin.
2. On the second matter, the dissipation of orbital energy in a binary system via
gravitational radiation: I am not sure myself whether there is anything to detect or not. There might even be an explicit explanation of how that radiation is emitted – or it might be explained largely by the drop in system energy. Does the energy stream out of some sort of chute or simply manifest itself through a changed orbital geometry? But I think it worth investigation. Seemingly less significant experimental physics has been performed over the years – and breakthroughs often seem to hide in such corners. E.g., take background microwave noise. We assume that that the barycenter of a system of masses has no tangible effects, but some things about GR vs. Newtonian gravity are distinct. The warping of space, the velocity limit of light, etc. Newton says a hollow sphere is one where a spacecraft can drift, GR says that the mass draws down into the center. The Einstein-Schwarzschild solution to the light’s bent path assumes something like a point mass and a singularity in the sun. And yet one would be laughed out of a colloquium these days if you claimed there was indeed a black hole in its center.
We turn over every rock looking for a means to power voyages to the stars. Why not take a closer look at binary system barycenters?
Re point 1. I am not clear what you are describing. For a true single light source, the the light that reaches another star light years away, will be a near parallel beam within the gravitational field of the star. That light will focus along the gravitational focal line. For our sun, from the minimum, about 550 AU to a reasonable maximum, about 1000 AU where only the widest radius of the Einstein ring can still work. After the focus point for any given ring radius, the light rapidly diverges.
I this scenario, there is no “grid” of high-intensity light. From the posts and papers on this subject, the light at the focus is still pretty weak.
What I thought you were originally getting at was the case of close binaries. If out sun was in a binary system with its companion orbiting 550-1000 AU away. out sun could act as a lens to create a near parallel beam of our companion star’s light. Still not intense, but clearly it would increase the apparent luminosity of our sun as observed from some distance. If our companion star was a very different stellar type, any observer in the line of that beam would see our sun become very bright with a rather confusing spectrum. It would look like a yellow G2 but have the strongest spectral lines from the hidden companion star.
A the companion star orbits our sun around their barycencenter, the beam would sweep slowly around the sky. The observer in another star system, whose star is also moving relative to our system, would therefore see a transient brightening of our system which would end as the beam swept past the observer.
This requires binaries to be separated within their relative focal lines. For equal mass stars, there would be 2 beams, in opposite directions. For unequal mass stars, only one beam. For unequal mass stars with eccentric orbits, the beam might appear from one star, then eventually appear coming from the other star. If either beam was observed from a distance, the binaries would appear to brighten at different times. In most cases, I would think the brightening would be a single transient, seen a few times at best, then never again.
However, with a galaxy full of binaries, with some fraction close binaries that could emit beams, and with those beams intersecting other star systems, it just might be the case that every so often the observer would see a transient brightening of a star.
For an advanced civilization, a bright em source could orbit a black hole, with the beam acting like a lighthouse beam, perhaps sweeping the galactic plane, indicating the presence of the BH. That beam might just have the bandwidth to offer an abridged Encyclopedia Galactica, or at least a Hitchhikers Guide to the Galaxy. With the rapid orbit around the BH. the beam would be seen by an observer a number of times before it disappeared. Inclining the orbit to the galactic plane might even provide wider coverage of the sky illuminating more star systems, and perhaps even revisiting the same stars every 250 my. Creating these lighthouse beacons for many BHs would increase the chances of a beam intercepting a star system with an extant technological civilization.
If this situation was possible, then we really need an all-sky observing telescope to monitor the heavens all the time just in case we happen to detect such an anomalous brightening. We could then use our own high-resolution telescopes to inspect the source star/system to determine if it might be a technological source rather than a serendipitous natural one. A monochromatic laser as the light source would be a giveaway, as would a series of pulses with prime number lengths, each pulse containing a message, preferably in pictures rather than a language.
A.T.,
Regarding the above about what I was driving at with respect to a single light source, here is a more detailed explanation than earlier:
—-
Instead of the binary Alpha Centauri and with its specific distance from us, let us have a Sol like star at a parsec distance…
Treating the Earth and Sun as a model, say they existed as a mirror image twin a parsec away and as a stand-in at this convenient modeling distance. An Earth would be as much as an arcsecond away from this sun. Ignoring obtaining a detailed image of the planet, were the SGL to collect light with a focus on the center of the stellar hemisphere, then the flux we experience as 1360 watts/ meter^2 at 1 AU would be diluted or attenuated by distance to a level 1/(206,000)^2 less intense. But the concept potentially collects and transmits what falls on half of 4 pi r^2 surface area of the sun,Pi r^2, if treated as flat. For sake of argument, if this is the projected surface with radius of 7e8 meters, the diffuse energy of a star similar to the sun (roughly Alpha Centauri A) has an area of 1.54e18 square meters for collection. The result is a beam of 49.3 gigawatt (!) intensity, assuming no “real world” dissipation. In terms of collection, moving a panel two kilometers “upstream” from the focus expands the projection to 1 meter dimensions, and so forth.
Whether this is the actual case, or not, the theory appears to allow for something like this, a notion a number of correspondents have already suggested or explored.
A star like the sun or Alpha Centauri A at a parsec’s distance would be a relatively intense case for our night sky. Elsewhere, assuming this model, there could be more intense sources such as A stars such as Sirius or white dwarfs doing the same duty and generating similar beams. The collimated beams would be very narrow and their passage through a point in the celestial sphere fleeting. But if they exist and are tracked, they would be something significant to contend with either as a hazard or as a source of energy.
OK, I think I understand what you are getting at. I think I was getting misled by your use of “collimated beams” that gave me an image of intense beams of energy cutting across interstellar space. I think what you are saying is that the focal line of about 500 AU in our system (start of focus to noise dissipation) represents a potential high-energy “beam”.
In practice, I believe that is not the case, as the focal area is kilometers on a side. Prior posts on this have indicated that a meter telescope still has to take time to collect enough photons to build an image of a planet, but IDK what the case would be for an image of the star – would it be billions of times as intense? If it was, and your 50 GW intensity was correct, it would fry a telescope at the focus, let alone the optics.
If the focal diameter is 10 km, then the intensity per m^2 is 1/7.5E7 th. This would reduce the intensity to 2/3 KW/m^2. If the focal area was increased to 100 km diameter, that would reduce to 6 W/m^2. Thus while the total energy of the “beam” could be great, its intensity would not.
But suppose your calculations are correct. Also, suppose that a 50 GW “beam” exists on the SGL with a 10 km diameter. Imagine the usefulness of that beam being available to accelerate a sail ship for up to 500 AU. This beam would be available for all directions opposite to stars in the sky within some radius from the sun, or intensities. It used to be said that humans could see about 2500 stars with the naked eye. Assume just 250 of those stars was bright enough to produce a decent focal energy beam. Then we could send sails in 250 directions to explore the local ISM . Just how fast would their terminal velocity be before stowing the sails for cruise?
But wait, there’s more. The same effect applies to target stars. If they are also aligned with a star, then their focal line beams could be used to decelerate a sail. No need to do a flyby, as the sail could slow down with both this energy, and the target star’s direct output in the system. This would allow for a rendezvous with a planet.
Of course, the changing alignments of the SGL beam would mean that it must be tracked to some extent, but is this a major issue given the acceleration period?
I need to do some calculations. If your BoE calculations are within an order of magnitude, maybe there is an article, even a paper to be written. I think this is a novel idea to explore.
You have stimulated my little grey cells. (apologies to Agatha Christie).
wdk
I looked at this before and commented about this on this site, I forget when.
The problem sits with the image formed as its the ratio of the focal distances, i do feel the centre of the image formed would be very intense but I was assured it would not be as the energy is spread out across the image. It may be enough to power a low power device but it is quite small. However white dwarfs especially Sirius b would offer a lot of energy indeed along the focal line, a celestial light sabre.
Some BoE calculations.
Source: “A Telescope at the Solar Gravitational Lens Problems and Solutions” Geoffrey Landis https://ntrs.nasa.gov/api/citations/20180002197/downloads/20180002197.pdf
Image size at focus = X0 (F/d) where X0 is planet size. For the same Earth-sized planet, this creates am image size of 12.5 km. For a star like th3 sun, d => 1.5E3 km.
d => ~= 1E14 km. F=> ~= 1E11 km
d/F => ~= 1E3
——————————————————–
Assuming the light of the star is diminished by distance, the flux reaching our sun is approximately the flux at 1 AU/ distance^2. For a star 10 ly distant,emitting light like our sun at around 1300 W/m^2, that ~= 1300*(1AU/10ly)^2 =~ 1300*E-10 W/m^2
But the Einstein ring is only a fraction of the area of the sun, at about 1% of the sun’s area at best. So the total flux concentrated in te image at 550 AU is:
(flux at sun)*ER area/image area.
From Landis’ paper, the image size = X0*(F/d). => X0*1E-3. If X0 radius ~= 700,000 km
the image radius is about 700 km. If the ER area ~= 1E-2 of the sun, and the image area => 1E-6 of the sun.
The flux/m^2 at the image = (flux at sun)*(sun area/image area)*(ER area/sun area)
=> 1300*1E-10*1E6*1E-2 => 1300*1E-6 => 1.3E-3 W/m^2
If that calculation is correct, then the flux at the image is about 1/1000th W/m^2. That is a very low value. OK for a telescope to image a star, but not for pushing even the lightest of sails as I speculated might be possible. The total energy within the image :
=>1300E-10*Pi*(700,000)^2 W => 2E2 KW.
This is far less than the 50 GW you calculate.
[I note that Landis’ has a light amplification formula for a planet in teh paper, but I am not sure I buy it It has a value of 6400x for an Earthlike planet orbit a str 10 ly away. But if you replace the planet with a star, the value for the star would be just 64x its flux as received at the sun. No idea how that formula was derived.]
Bottom line:
We are calculating vastly different values for the energy of the energy at the focus for a distant star, as well as the energy density given the likely size of the focal image.
Simpler version:
Same scenario. A duplicate of our sun 4 ly away.
I ignore the issue of the Einstein Ring and assume the sun just acts as a convex lens.
1. The intensity of the duplicate stars flux/m^2 at aour sun is:
E1 = E0/d^2 w/M^2 [1] where E0 is the flux at 1 AU and d is the distance to our sun in AU.
2. The flux at our sun is concentrated in the image of the star at the focal point.
Using Taloff’s eqn for image size:
X1 =X0(F/d) where X0 = star’d diameter, X1 is the image diamter, and F is the focal length in AU.
Rearranging X0/X1 = d/F
For the area (X0/X1)^2 = (d/F)^2 [2]
This is effectively the concentration of the flux arriving at the sun into a focal image.
3. The 2 eqns are combined to:
E1 = (E0/d^2)(d^2/F^2) => E0/F^2. [3]
So now we see that the image intensity is only a function of the focal length. Distance is now irrelevant.
Using 1300 W/m^2 for E0 and 550 AU for teh focal length, we can see that the flux at the image is a tiny fraction of the stars flux at 1 AU.
e.g 1300/(550^2) => 0.0043 W/m^2 [4]
So clearly there is no intense beam at the focal line.
Can this be rescued by a different type of star? The energy flux per unit area emitted by a star is a function of its absolute temperature. The hottest stars include teh giant Rigel at 12,100 K and teh white dwarf Sirius B at 25,000 K.
Using Sirius B, the energy flux increase as a ratio of the sun
E_rigel/E_sun: = 25^4/5.8^4 = 345.
Plugging in to result [4] we get 1.48 W/m^2, just over 1/1000th of E0.
While the runway for accelerating a solar sail is long, there is also th eissue of a falling intensity as F increases, which average 1/2s the flux at 550 AU over the distance to 1100 AU.
This buys you nothing, so no free lunch in powering a sail using the light from a hot star focused at the SGL.
However, it may still work for stars where the focal line is close to the star, as F^2 is now much lower.
e.g. Sirius B has a focal line starting around 0.055 AU. So scaling implies a launch ramp or another 0.055 AU.
But at 0.055 AU, the flux at the focal point for another similar star is now
(1300*345*.0043)/(0.055)^2 = 8916 W/m^2.
But if you could get a sail that close to Sirius B, why not just use the star’s flux directly, which would be 232x greater, with a longer launch ramp?
In summary, the use of a gravitation focal line to accelerate a sail is a non-starter because the flux intensity at the focus is extremely low and is not even close to being compensated by the much longer acceleration phase.
A.T.,
Please excuse my delay. Over extended over here.
Admittedly, there is a whole lot of reasons to be skeptical of the gigawatt scenario described. Others noted reasons as well. So, proceeding based on hypotheses…
I believe there are a couple of divergences in our modeling. And perhaps the nature of the image transmitted if one aligns with a stellar target – or an exoplanet in its vicinity. From one to ten parsecs, there are significant arc second differences between the center of a star and an orbiting exoplanet in the HZ zone.
Also, there is the issue of whether the FOV extends over the entire area blocked by the sun from 550 AU – or something narrower.
But I suspect that to get an image of an exoplanet it is desirable to have an offset, and then continue to track focusing on the planet as the target. I am assuming a field of view based on the celestial circle carved by the solar radius at 550 AU. For a nearby (1 to 10 parsecs) both a star and an HZ exoplanet can be contained within it.
Making that distinction, focusing directly on the star would mean that stellar light would dominate – unless a stellar “coronagraph” is implemented to block it out. Though this could be a difficult proposition if our assumptions are correct. But the load could be reduced once planet position is discerned.
So, collecting the light of a star like the sun at 1 parsec away, the surface temperature at 700,000 km radius is about 5800 K. If this flux source is expanded ( no adds or subtractions) to 1 AU, the effective temperature is
400K. This is akin to 1360 watts/meter squared. Correspondingly, in the absence of a spherical lens, this energy would be further diffused at 1 parsec’s distance from the source to roughly ( 1/206,000)^2. of the 1 AU value.
I think I used the wrong ratio earlier, top of my head. But for reference,
a parsec is about number ofdegrees/ radian ( 57.3) times number of seconds per hour, or arc seconds per arc minute, arc minute in angular measure per “arc hour”.
OK, so that substantially reduces the intensity of radiative flux from 1360 watts/square meter to 3.2 e-8 watts/ square meter. Now, let’s assume the spherical lens is collecting over a pi radius square area of a solar cross section:
700 hundred million meters squared x pi:
1.5393 x 10 to the18 square meters.
The signal is amplified to 49 gigawatts – unless there are dissipating elements in the system.
Someone might argue that the stellar source light is a point source. Still would the operation of other telescopes is based on collecting photons, increased with aperture. As far as I can tell, based on a principle similar to what I just described, this is what would occur. If an exoplanet is targeted, then a similar collection of photons is undertaken, though I would recommend a focus on the exoplanet rather than the star. To remove extraneous light data and not to burn the optics out.
This is all very confusing. Let’s back back to basics.
1. Conservation of energy. The energy collected at the SGF telescope cannot be greater than the energy falling on the objective lens (Einstein ring or arc). It doesn’t matter how we deal with it.
2. Power is the rate of energy (first time derivative). 1 watt is 1 J/s, or 0.01 J over 100 seconds or 100 J over 0.01 seconds.
3. Flux is not energy or power. Flux is power flowing over an area. The smaller the area over which a radiant power is concentrated, the higher the flux. That’s how mischievous little imps like me used to incinerate insects with a magnifying lens. The concentration to a higher flux does not alter the power delivered.
4. For an Einstein ring or conventional lens there is a maximum flux at the focal point. That is because real sources are not points. The diameter of the image limits the flux.
HTH.
wdk,
The energy would be spread over the image of the star at the focal point, the magnification been the ratio of the distance to the star and the focal point of image in our case 550 AU. Although the flux is quite small in the milli watts it should be enough to power the bridge communicator if nano electronic are used. It would be interesting if these ideas could be tested with some ray simulation software as there maybe a more concentrated central beam of light with more power.
The light for the distant star is only acquired from the Einstein ring, not the whole surface of the focusing star. So the total energy is much reduced.
A telescope still needs a chronograph to exclude the light from the sun which is by far the strongest light source.
The 50 GW energy is spread out over the image size. For a planet, Matloff indicated a diameter of 12 km. Using the same formula I get 1400 km for a sun-like star. So the 50 GW is reduced to 1.66E-8 W/m^2. If the energy only from the Einstein ring is assumed, it might be several orders of magnitude lower.
However, I think you may be correct about the shape of the image. While the impression I get is that it is smeared out over the image area, the image may be more of a ring that is then deconvolved to extract the true image of the exoplanet or star. In which case, I would argue that there is no need to reduce the energy/m^2 from the baseline calculation but rather to increase it several orders of magnitude with the focused image an annulus. But even in this case, the energy seems very low to me. I would also stand by my belief that the actual energy reaching the focus via the ER is a fraction of the 50 GW you estimate, perhaps 0.5 GW, but this may be restricted to an annulus image at the focal point which would look like a dark circle with a thin bright perimeter but with a much more intense circle of light inside that ring coming directly from the sun with an intensity reduced to that at 550 AU.
Alex the energy is enough to have a BER of near zero so we could power our space craft without the need for onboard power.
A.T.,
As Project points out, LIGO detects a disturbance in space when something like two condensed objects collide or merge. And I would suppose that if something drastic occurred in the Hulse-Taylor pulsar’s vicinity, LIGO would detect that too. So, I would say that this is not simply a matter (sic) of potential energy leakage. However, crossing that bridge, I would gladly defer to the specialists on such matters as to what the grav wave frequency would be. Of course, with photons emitted from particles such as electrons, we associate them with the particles themselves, reducing their energy states – but on the other hand, we don’t have a clear notion ( in most cases) of where the electrons are …
A.T.,
Got your message on this. One way to look at this is: what it is, it is. And that includes the likelihood that these phenomena will not behave as BOE calculations suggest. More modeling or experiments required. But to explain my calculations in another way: The 1360 watts/meter^2 solar flux intensity we experience locally is a T^4 R^2 relation from the sun’s surface temperature of 5800 K to the 400 locally of 1 AU. Play the same game with the sun at 1 parsec and you have a spherical flux at 1 parsec WHEN collected by a solar area receiver, capable of producing 50 gigawatt. You mention the Einstein ring. That might just be a more reasonable limit. However, when i read the AAAS Science write up Einstein provided in the 1930s, he was only looking at a ray of light from a star. That did not necessarily preclude the collection we are talking about, however.
I also agree with you that the tracking involved for collecting the resulting beam would be taxing. And some of the intermediate experiments could be interesting too. E.g., when Pound and Devka did the time dilation experiments due to depth in a gravity field back in the 1950s, they were not anticipating GPS application.
I just did another simpler calculation using flux intensities to come to the conclusion that the flux at the focal point is minuscule. (see reply to my comment above).
Also, using your 50 GW value of collected photons, the flux density spread out over the image area is about 0.025 W/m^2 – assuming Matloff’s equation is correct.
The Einstein ring area is a fraction of the sun’s area, perhaps just 1%, which might reduce the flux density by a further 2 orders of magnitude.
So I don’t see any case where the SGL creates an intense beam even if the total energy is high because it is just too diffuse. It reminds me of the O’Neill suggestion for beaming solar power to Earth using microwaves. The ground antennas had to be huge to keep the intensity so low that it wouldn’t cook birds flying through the beam. As long as the antenna fully absorbed the microwaves, you could still use the sunlight to grow crops, or grass, and have grazing animals happily living underneath the antennas while the energy was harvested for powering civilization.
As far as using the flux at the SGL to launch solar sails, the very low intensity is a bust. It does almost nothing to accelerate a sail. Even using a very hot star like Sirius B as the distant star to focus on to increase the baseline flux intensity does not buy enough extra energy for the sail. So that idea is a bust too. Oh well… Better to travel the 8.6 ly to Sirius B and launch the sails directly from the star. The earlier post on using flybys of hot stars to accelerate sails might well target Sirius B as a potential [huge] accelerator.
I really need to read Maccone’s paper on communication to understand the gains from beaming from the SGL to a target to reduce power consumption for interstellar beaming. It may well have useful insights for the reverse situation, e.g. a close binary with the companion inside the SGL inner and outer bounds creating beams that can be seen throughout the galaxy, even beyond. That must be generating lots of beams in galaxy full of close binaries, with the beams pointed in random directions and observed as “transients”. We seem to have no problem observing gravitational lensing of galaxies which will not be transient, so I have to wonder if the sky is full of beams of which we may observe a few by chance if we are looking everywhere.
Alex at the 0.05AU start of the focal line Sirius b I believe has only 12 times the sun illumination but if it focuses light from Sirius A its about 82 times Sol’s at the nearest approach. Perhaps some stars may allow us to use the little power received to power the communicator bridges. The white dwarf also allows us to concentrate a lot of power using the bending process if a laser system is used. If say the power from Sirius A is converted to a laser light and then focused by bending around the WD we would have a very powerful beam accelerator indeed. As a tech species getting control over a white dwarf would be a great coup indeed, the Sirius system twice so !
Bear in mind that the energy focused by Sirius B is only from the Einstein Ring, a fraction of the energy impinging on the star.
I can see that a focal lens of Sirius B could then be made into a parallel beam with another lens, or collectors across the image and used to power a phased laser array.
Sirius B is 16 AU from Sirius A, so any light reaching Sirius B for focusing is already about 1/250th the intensity of the light near Sirius A. Then the total energy is further reduced by the fraction of light bent by the Einstein ring to reach a focal point behind Sirius B. As Sirius A is a large star, the light from the star will not be parallel at Sirius B so the focal image will be large. The area of the lens of the collector array will be larger than if the star was more like a point source.
Probably worth doing the numbers to determine if any arrangement buys you a more powerful beam than the one powered directly from collectors close to Sirius A.
[The whole point of the communication bridge is that the radio source travels across interstellar space as a perfectly parallel beam to be refocused at the destination, therefore mitigating the problem of the 1/r^2 reduction of beam strength of a non-parallel beam, even a laser. The focal length is much less than the interstellar distance which makes this attractive. Similarly, the gravity lens provides a lens of immense size to increase the resolution of the focused image, even as that image is very large and needs to be sampled and the exoplanet image deconvolved from the light in the Einstein ring. What you are buying is the resolving power in this case.]
At say 16 AU from Sirius A we would have 1/256 × 25 x 1300=127 W per square meter which will be bend towards a focal point at 0.05 AU. The magnification at 16 AU distant would be 320 times at 0.05 AU. So the whole image of Sirius A would be shrunk to a diameter of about 7200 km at 0.05 AU surely all that 127 W per square passing Sirius b will be concentrated down into that 7200 km diameter image. We only see the Einstein rings size because of the size of the aperture of looking at the image, an aperture the size of the image, 7200 km, would see an Einstein ring as big in area as the object, Sirius A.
If one looks at the classic diagram of a gravity lens, only the parallel rays from the source object that pass by the gravity source are focused. Therefore the energy that can be focused is the area of the Einstein Ring at any point along the SGL.
Any non-parallel ray will be focused as a point further along the SGL. I concede that a non-parallel ray will focus at the same point as a parallel ray from an ER with a greater radius once beyond the minimum focal point, albeit that the total image size increases.
As the initial idea of using the lens as a telescope was to use the photons to build an image with the resolution of the size of the ER, this is not so relevant with focusing energy. All that we are concerned with are the photons that can be concentrated from the ER [or ERs?], and how that energy is distributed at the focus – as a circle or ring and the distribution of the energy flux across the image. IDK what the answer is.
Note my next comment that points to the reference posted by Jeff Wright about power beaming that may answer the question.
I do find the magnification astonishing able to detect a 1 W laser beam from proxima’s distance. Also able to detect features on a neutron star if the wavelength is low enough, possible gravity wave detector?
https://arxiv.org/abs/2210.01568
In the current post on “Pinched Beams”, Jeff Wright has posted a link in teh comments about power beaming. It is by Maccone’s colleague and is very math-heavy. The claim is that using a gravity lens is a useful way to send power across interstellar space as the parallel beam is not divergent. However I cannot find any example values in a scan of the text, and it needs someone with good math skills to understand what he has done and what some concrete values would be.
Equation 44 for a two lens system indicates that even with 1 W been sent only approx 2.5 e-11 of that watt will be received, but there are a number of parameters that can be altered to improve that such as diameter of the reciever, telescope, wavelength, distance etc.
Increasing the transmitter and receiver sizes close to 10 km in diameter offer near perfect transmission of power according to the equations. There are a lot of squared functions in the equation that could be taken advantage of to improve transmittance.
Been off-line on this matter for a while. And note that there is still considerable controversy. But I suspect that that is OK. We have tossed around some interesting models of what is going on: sometimes ( including my case) based on misunderstanding, and in other instances, some interesting issues. Worth mulling as it were.
In my own case, I hope to better understand certain parts of the flow chart for such a device: the lens field of view, the collection of light and its transform into an annular signal eventually focused at a point. And then deconvoluted.
Best regards,
WDK