Every now and then I run into a paper that opens up an entirely new perspective on basic aspects of space exploration. When I say ‘new’ I mean new to me, as in the case of today’s paper, the relevant work has been ongoing ever since we began lofting payloads into space. But an aspect of our explorations that hadn’t occurred to me was the obvious question of how we coordinate time between Earth’s surface and craft as distant as Voyager, or moving as close to massive objects as Cassini. We are in the realm of ‘time transformations,’ and they’re critical to the operation of our probes.
Somehow considering all this in an interstellar sense was always much easier for me. After all, if we get to the point where we can push a payload up to relativistic speeds, the phenomenon of time dilation is well known and entertainingly depicted in science fiction all the way back to the 1930s. But I remember reading a paper from Roman Kezerashvili (New York City College of Technology) that analyzed the relativistic effects of a close solar pass upon a spacecraft, the so-called ‘sundiver’ maneuver. Kezerashvili and colleague Justin Vazquez-Poritz showed that without calculating the effects of General Relativity induced by the Sun’s mass at perihelion, the craft’s course could be seriously inaccurate, its destination even missed entirely. Let me quote this:
…we consider a number of general relativistic effects on the escape trajectories of solar sails. For missions as far as 2,550 AU, these effects can deflect a sail by as much as one million kilometers. We distinguish between the effects of spacetime curvature and special relativistic kinematic effects. We also find that frame dragging due to the slow rotation of the Sun can deflect a solar sail by more than one thousand kilometers.
Clearly, what seem like tiny effects get magnified as we examine their consequences on spacecraft moving under differing conditions of velocity and gravity. The measurement of time is a key aspect of this. And even the tiniest adjustments are critical if we are to build communication networks that operate accurately even in so close an environment as that between the Earth and the Moon. Thus the occasion for this musing, a paper from the Jet Propulsion Laboratory’s Slava Turyshev and colleagues that discusses how the effects of gravity and motion can be understood between the Earth and the network of assets we’re building around the Moon and on its surface. Exploration in this space will depend upon synchronizing our tools.
The Turyshev paper puts it this way:
As our lunar presence expands, the challenge of synchronizing an extensive network of assets on the moon and in cis-lunar space with Earth-based systems intensifies. To address this, one needs to establish a common system time for all lunar assets. This system would account for the relativistic effects that impact time measurement due to different gravitational and motion conditions, ensuring precise and efficient operations across cislunar space.
And in fact a recent memorandum from the White House Cislunar Technology Strategy Interagency Working Group was released on April 2 of this year noting the “policy to establish time standards at and around celestial bodies other than Earth to advance the National Cislunar S&T [Science and Technology] Strategy.” So here is a significant aspect of our growth into a cislunar culture that is growing organically out of our current explorations, and will be critical as we expand deeper into the system. One day we may go interstellar, but we won’t do it with a Solar System-wide infrastructure.
As an avid space buff, I should have been aware of this all along, especially since gravitational time dilation is easily demonstrated. A clock on the lunar surface, for example, runs a bit faster than a clock on Earth. Because time runs slower closer to a massive object, our GPS satellites have to deal with this effect all the time. Clearly, any spacecraft moving away from Earth experiences time in ways that vary according to its velocity and the gravitational fields it encounters during the course of its mission. These effects, no matter how minute, have to be plugged into operational software adjusting for the variable passage of time.
So moving from time and space coordinates in one inertial frame (the Earth’s surface), we need to reckon with their manifestation in another inertial frame, that aboard a spacecraft, to make clocks synchronize accurately and hence enable essential navigation, not to mention communications and scientific measurements. The necessary equations to handle this task are known in the trade as ‘relativistic time transformations,’ and it’s critical to have a reference system like the Solar System Barycentric coordinate frame (SSB) that is built around the center of mass of the Solar System itself. This allows accurate trajectory calculations for space navigation.
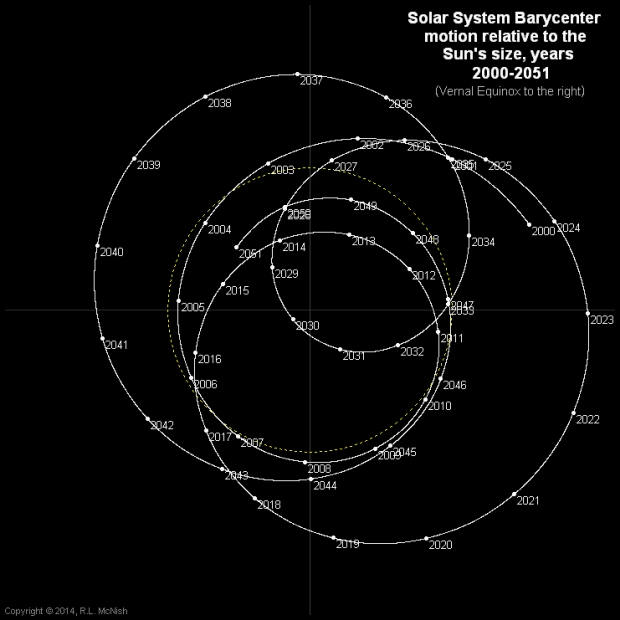
Image: The complexity of establishing reference systems for communications and data return is suggested by movements in the Solar System’s barycenter itself, shown here in a file depicting its own motion. Credit: Larry McNish / via Wikimedia Commons.
As you would guess, the SSB coordinate frame has been around for some time, becoming formalized as we began sending spacecraft to other planetary targets. It was a critical part of mission planning for the early Pioneer probes. Synchronization with resources on Earth occurs when data from a spacecraft are time-stamped using SSB time so that they can be converted into Earth-based time systems. Supervising all this is an international organization called the International Earth Rotation and Reference Systems Service (IERS), which maintains time and reference systems, with its central bureau hosted by the Paris Observatory.
‘Systems’ is in the plural not just because we have an Earth-based time and a Solar System Barycentric coordinate frame, but also because there are other time scales. We use Coordinated Universal Time as a global standard, and a familiar one. But there are others. There is, for example, an International Atomic Time (TAI – from the French ‘Temps Atomique International’), a standard that is based on averaging atomic clocks around the world. There is also a Terrestrial Time (TT), which adds to TAI a scale reflecting time on the surface of the Earth without the effect of Earth’s rotation.
But we can’t stop there. Universal Time (UT) adjusts for location, affected by the longitude and the polar motion of the Earth, both of which have relevance to celestial navigation and astronomical observations. Barycentric Dynamical Time (TDB, from ‘Temps Dynamique Barycentrique’) accounts for gravitational time dilation effects, while Barycentric Coordinate Time (TCB, from ‘Temps Coordonné Barycentrique’) is centered, as mentioned before, on the Solar System’s barycenter but excluding gravitational time dilation effects near Earth’s orbit. All of these transformations aim to account for relativistic and gravitational effects to keep observations consistent.
These time transformations (i.e., the equations necessary for accounting for these differing and crucial effects) have been a part of our space explorations for a long time, but they hover beneath the surface and don’t usually make it into the news. But consider the complications of a mission like New Horizons, moving into the outer Solar System and needing to account not only for the effects of that motion but the gravitational time dilation effects of an encounter not only with Pluto but the not insignificant mass of Charon, all of this coordinated in such a way that data returning to Earth can be precisely understood and referenced according to Earth’s clocks.
The Turyshev paper focuses on the transformations between Barycentric Dynamical Time and time on the surface of the Moon, and the needed expressions to synchronize Terrestrial Time with Lunar Time (TL). We’re going to be building a Solar System-wide infrastructure one of these days, an effort that is already underway with the gradual push into cislunar space that will demand these kinds of adjustments. These relativistic corrections will be needed to work in this environment with complete coordination between Earth’s surface, the surface of the Moon, and the Solar System’s barycenter.
The paper produces a new Luni-centric Coordinate Reference System (LCRS). We are talking about a lunar presence involving numerous landers and rovers in addition to orbiting craft. It is the common time reference that ensures accurate timing between all these vehicles and also allows autonomous systems to function while maintaining communication and data transmission. Moreover, the LCRS is needed for navigation:
An LCRS is vital for precise navigation on the Moon. Unlike Earth, the lunar surface presents unique challenges, including irregular terrain and the absence of a global magnetic field. A dedicated reference system allows for precise positioning and movement of landers and rovers, ensuring they can target and reach specific, safe landing sites. This is particularly important for resource utilization, such as locating and extracting water ice from the lunar poles, which requires high positional accuracy.
Precise location information through these time and position transformations will be, clearly, a necessary step wherever we go in the Solar System, and a vital part of shaping the activity that will build that system-wide infrastructure so necessary if we are to seriously consider future probes into the Oort Cloud and to other stars. Turyshev and team refer to all this as the establishment of a ‘geospatial context’ within which the placement of instruments can be optimized, but the work also becomes vital for everything from the creation of bases to necessary navigational tools. For the immediate future, we are firming up the steps that will give us a foothold on the Moon.
The paper is Turyshev et al., “Time transformation between the solar system barycenter and the surfaces of the Earth and Moon,” now available as a preprint. If you want to really dig into time transformations, the IERS Conventions document is available online. The Roman Kezerashvili paper cited above is R. Ya. Kezerashvili and J. F. Vazques-Poritz, “Escape Trajectories of Solar Sails and General Relativity,” Physics Letters B Volume 681, Issue 5 (16 November 2009), pp. 387-390 (abstract).



I’m trying to wrap my head around some of this. I know that velocity affects time and we can even detect that by the Doppler effect on light. I know that gravity affects time, again detectable by light wavelengths. What I don’t know is the issue of frames of reference. For example, a satellite orbiting the Earth is running slower due to the velocity, but is is also offset by running slightly faster as it is higher in the gravity well? Similarly, a spacecraft traveling to the outer planets will be traveling so that the gravity well is lessening (faster time?) yet it is also reducing velocity (also faster time?) . If it enters a gravity well like Jupiter, do both the new gravity well and increased velocity slow time?
For a spacecraft in the ISM, well away from the gravity well of stars, the time should be dependent on velocity alone. But we know it is still within the gravity well of the galaxy. What effect does that have? It is also rotating around the galaxy at a far higher velocity than with respect to the nearby stars. Does that have any effect? IOW, which frames of reference are relevant to do the calculations? [ Do I have to read the paper to find out, or is there a simple way to tease these effects apart? ]
This is a deeply informative piece. The idea of relativistic time corrections is fairly widely known for the GPS system, but all the other pieces to the puzzle are not, and news to me. The fact that several pieces are at the Paris Observatory is a holdover from work there starting in the 1880s, I believe.
The map of the barycenter motion shows that the time elapsed from the start of a loop to its return to the “same side” of the next loop is about 12 years (example: 2029 to 2042), which I take as due primarily to influence of Jupiter. Very interesting!
Time, like space, is perceptible only in the interval between two points. A photon leaving the Andromeda (or more remote) galaxy for the Earth at lightspeed will perceive its arrival here at the very instant at which it commenced its journey. In its frame of reference velocity has been stretched and time has been squashed, both to the max.
Likewise a spaceship having passed through the event horizon of a “mega” black hole (prior to spaghettification) will have time pass so slowly that eons of its time may take fractions of an outside observer’s second. Gravity slows their time down so much that tiny distances take so long to traverse that they don’t seem tiny anymore.
Yes, the time dilation is due to people on the surface of the Earth being in a gravity well so time moves slightly slow than spacecraft in orbit. GPS matters for locating the accurate position people on the surface of the planet like the Earth and the Moon as apposed to anything in orbit around it. If one has a hyperbolic trajectory or escape velocity none of that matters. Inertial and non inertial frames and Lorentz transformations do matter. The galaxy rotates at 500,000 miles per hour. Relativistic time dilation does not matter until one reaches one tenth light velocity. The orbits of the planets precess according to general relativity and that includes the Sun’s barycenter. I image that is factored into the long term accurate positions of the planets by the Jet Propulsion laboratory. I don’t get the Solar System Barycentric coordinate frame (SSB) idea though that is how it is used to predict accurate trajectories for our pioneer probes. I thought is was SSB was used for Astrometry.
Relativistic time dilation has to be accounted for well below 10 percent of lightspeed. We account for it with our current space probes and the software that empowers them. That’s very much what my article is about.
There are a variety of effects of gravitation to consider, however they tend to fall into one or both of these two categories:
– Long term error accumulation (e.g. GPS), where accuracy is paramount
– Short term errors at high frequencies and data rates
For example, when a spacecraft makes a close approach to a planet. Additional clock and oscillator sync is needed for DSN to lock onto the signal, for both reception and transmission, especially if the bandwidth is small due to SNR. The signal can shift right outside the filters!
At high data rates, the framing of bits will accumulate errors until sync is lost. The faster the rate the sooner it happens, and it’s worse at the GHz frequencies where spacecraft communication is done. For example, the baseband rate may be 1 Mbps and the additional error due to GR from a close approach will eventually corrupt every data frame. Receivers and transmitters must predict the time base, additional data rate change and frequency shift due to GR, in addition to the multitude of other factors.
That is routine.
Choosing a common reference clock is necessary, but it matters less what it is than that all agree. Choosing the reference matters in two respects: TOD/clock time, and relative duration of a second, whether calculated or measured. In any one application, one of these may matter more than the other. The impact of GR is universal and affects any pair of observers that are not in the same location and co-moving, whether inertial or accelerated.
“The impact of GR is universal and affects any pair of observers that are not in the same location and co-moving, whether inertial or accelerated.”
Exactly so!
Wikipedia article on orbital speed effect on time vs gravitational effects.
Time dilation
Here is the atomic clock of Paris and a web page that allows to see the sychronization of your computer in the thousandth of a second which is already huge…. and we are on earth! ;) Imagine then the compensations that would be needed to coordinate objects in deep space dotted with good big black holes and other neutron stars ! ;)
https://www.observatoiredeparis.psl.eu/-heure-legale-francaise-.html?lang=fr (english version available)
https://heurelegalefrancaise.fr/index.html?lang=en
From a technical point of view, we have a first line of research which is the cooling of our computers: more precision because more parameters also means more heat with our current technolgies. Will it be necessary to move towards superconductivity or other “quantum computers”?
will have to invent a new system of time reference, no longer in relation to our environment but for example by adopting a reference base like that of the supermassive black hole of our galaxy and then deducing time expansion scales according to other masses? it’s just an idea…
It reminds me of the Apollo 11 on-board computer whose computers are now thousands of times more powerful.
Very interesting. Thanks Paul
Over sufficiently large expanses or sufficiently precise measurements, both time and space are compressible,expandable and deformable with sufficient force.
The Strange Case of Quantum Time Loops And Testing Backward Time Travel
The big question is when, where and whether we might acquire control over the needed forces.
for me the question comes back to N. Kardashev and to pass in civilization of type II or III which means a technological evolution to master powerful sources of energy…
From a philosophical point of view, nothing says that the human species is predisposed to this; it is a somewhat pretentious anthropocentric vision in front of the powerful universal forces no ? but we have the right to dream ;)
I need some help with a thought experiment on GR and time.
Assume we are in the center of a homogenous universe defined bt the speed of light horizon. All the mass in the universe is nullified by being at the center so we have no gravitational slowing of time. Further, assume we are in intergalactic space so that there is effectively 0 net gravitational attraction of any nearby heterogeneity of mass, say from a galaxy, star, rogue planet, nebula, etc.
If we compare clocks to anywhere else in space, our clock runs the fastest. Is that correct, or not?
Second. Imagine that we have 2 entangled particles. One is on earth, the other the moon. Clocks normally run slightly faster on the moon. But how does entanglement affect the 2 entangled particles. Are their respective clocks also different or now forced to be the same?
I apologize for my ignorance in this matter, but GR physics is not something I have fully understood beyond the popsci basics.
@Alex,
I would answer yes to the first question: our clock would work faster than the others in this homogeneous universe out of gravity because influenced by the central mass of the universe but it does ask two other questions:
What would be the reference time that we would have to use? that of the center subject to gravity or the other, that of zero gravity (or almost since the entire mass of the universe will necessarily have an influence on time regardless of the distance from the center at least if we reason in Einstein’s physics)?
What would be the notion of time in such a universe without influence of gravity? We can imagine that at the limit of horizon we would have a time almost equal to zero in other words a frozen universe? It makes no sense…
let’s go further: a star is born and explodes as a supernovea on our horizon at “zero” time: what would the observer see in the center of the universe: the star at its birth, or at its death? Would he see slow or fast? Would he only see something? your universe would be rather nightmarish but the thought experience is fun.
To answer the second question, I think we should define a 3rd referential. or go in a universe with 10 or 15 dimensions and there I am not able:)
Alex you can never be at the centre of the universe, it’s as if the entire universe is on an ever accelerating bubble. You can only see the universe relative to other parts at the speed of light limit, an horizon if you like.
First off, the universe you posit is impossible. However it was generally believed to be the case before we knew better. Einstein quickly realized that after developing GR and introduced λ, a non-zero term, in essence a constant of integration. Its purpose (with value to be determined at the time) was to prevent the catastrophe of all those masses from attracting and collapsing together. Not long after, Einstein realized his mistake when it was discovered the universe was expanding. Of course, λ has a renewed focused in modern cosmology. But that’s another story.
The universe has no clocks! This may be a difficult idea for some to accept. All we have are the laws of physics and measurements. We build devices according to those laws that, by suitable choice of a physical process, measure time. Photons and other particles don’t wear wristwatches!
If I build a clock and you build a clock, and we then establish that they are synchronized, we are in a position to measure time, after a fashion. We can read the measurement of our own clocks and each other’s. In practice the latter can be quite difficult, but we can run with it for a thought experiment. Imagine that we can measure the tick-tocks at a distance.
Assume that you an I are in this flat (momentarily stable) cosmos and far from any masses, when we measure the ticking of our own and each other’s clocks, they will be in sync. The sum of those ticks (the time of day, if you like) will not agree because it takes time for the ticks to travel between us, and that’s true no matter how close we may be. If you want to be really pedantic about it, they will not be in sync because both are in the gravity wells of our own bodies and we likely don’t have the same mass!
As soon as you start moving (a period of acceleration and an optional return to inertial motion) we will measure the ticks as falling out of sync. If your net motion is towards me, I will measure your clock ticking faster. That is not even considering relativistic effects. I’ll leave the rest as an exercise.
QM treats spacetime as a background, not integrated into the theory: we don’t yet (maybe never) have a GUT. Particles, entangled or not, travel accordingly. If we are in relative motion, or in different gravitational wells, measured travel time and, in the case of photons, wavelength will be affected. When you measure the entangled photon I send you, you may then send me a message telling me what you measured and when according to your clock. I can then do some calculating if I know the particulars of our locations, motions and gravitational environments. There is no universal clock to provide the one true answer. All we can do is measure physical phenomenon.
Is this helpful?
Just as every point on the surface of a sphere is a center for the surface, so too every point in a hypersphere is a center for that hypersphere, and presuming homogenous isotropy throughout, any point will have no gravitational distinction from any other point within that hypersphere.
Entanglement makes itself manifest “instantly” in the other particle when one particle of a pair is measured. However, defining “instantly” at a remove of billions of light-years may be quite problematic.