Centauri Dreams
Imagining and Planning Interstellar Exploration
SETI and Gravitational Lensing
Radio and optical SETI look for evidence of extraterrestrial civilizations even though we have no evidence that such exist. The search is eminently worthwhile and opens up the ancillary question: How would a transmitting civilization produce a signal strong enough for us to detect it at interstellar distances? Beacons of various kinds have been considered and search strategies honed to find them. But we’ve also begun to consider new approaches to SETI, such as detecting technosignatures in our astronomical data (Dyson spheres, etc.). To this mix we can now add a consideration of gravitational lensing, and the magnifications possible when electromagnetic radiation is focused by a star’s mass. For a star like our Sun, this focal effect becomes useful at distances beginning around 550 AU.
Theoretical work and actual mission design for using this phenomenon began in the 1990s and continues, although most work has centered on observing exoplanets. Here the possibilities are remarkable, including seeing oceans, continents, weather patterns, even surface vegetation on a world circling another star. But it’s interesting to consider how another civilization might see gravitational lensing as a way of signaling to us. Indeed, doing so could conceivably open up a communications channel if the alien civilization is close enough, for if we detect lensing being used in this way, we would be wise to consider using our own lens to reply.

Or maybe not, considering what happens in The Three Body Problem. But let’s leave METI for another day. A new paper from Slava Turyshev (Jet Propulsion Laboratory) makes the case that we should be considering not just optical SETI, but a gravitationally lensed SETI signal. The chances of finding one might seem remote, but then, we don’t know what the chances of any SETI detection are, and we proceed in hopes of learning more. Turyshev argues that with the level of technology available to us today, a lensed signal could be detected with the right strategy.
Image: Slava Turyshev (Jet Propulsion Laboratory). Credit: Asteroid Foundation.
“Search for Gravitationally Lensed Interstellar Transmissions,” now available on the arXiv site, posits a configuration involving a transmitter, receiver and gravitational lens in alignment, something we cannot currently manage. But recall that the effort to design a solar gravity lens (SGL) mission has been in progress for some years now at JPL. As we push into the physics involved, we learn not only about possible future space missions but also better strategies for using gravitational lensing in SETI itself. We are now in the realm of advanced photonics and optical engineering, where we define and put to work the theoretical tools to describe how light propagates in a gravity field.
And while we lack the technologies to transmit using these methods ourselves (at least for now), we do have the ability to detect extraterrestrial signals using gravitational lensing. In an email yesterday, Dr. Turyshev offered an overview of what his analysis showed:
Many factors influence the effectiveness of interstellar power transmission. Our analysis, based on realistic assumptions about the transmitter, shows that substantial laser power can be effectively transmitted over vast distances. Gravitational lensing plays a crucial role in this process, amplifying and broadening these signals, thereby increasing their brightness and making them more distinguishable from background noise. We have also demonstrated that modern space- and ground-based telescopes are well-equipped to detect lensed laser signals from nearby stars. Although individual telescopes cannot yet resolve the Einstein rings formed around many of these stars, a coordinated network can effectively monitor the evolving morphology of these rings as it traces the beam’s path through the solar system. This network, equipped with advanced photometric and spectroscopic capabilities, would enable not only the detection but also continuous monitoring and detailed analysis of these signals.
We’re imagining, then, an extraterrestrial civilization placing a transmitter in the region of its own star’s gravitational lens, on the side of its star opposite to the direction of our Solar System. The physics involved – and the mathematics here is quite complex, as you can imagine – determine what happens when light from an optical transmitter is sent to the star so that when it encounters the warped spacetime induced by the star’s mass, the diffracted rays converge and create what scientists call a ‘caustic,’ a pattern created by the bending of the light rays and their resulting focused patterns.
In the case of a targeted signal, the lensing effect emerges in a so-called ‘Einstein ring’ around the distant star as seen from Earth. The signal is brightened by its passage through warped spacetime, and if targeted with exquisite precision, could be detected and untangled by Earth’s technologies. Turyshev asks in this paper how the generated signal appears over interstellar distances.
The answer should help us understand how to search for transmissions that use gravitational lensing, developing the best strategies for detection. We’ve pondered possible interstellar networks of communication in these pages, using the lensing properties of participating stellar systems. Such signals would be far more powerful than the faint and transient signals detectable through conventional optical SETI.
Laser transmissions are inherently directional, unlike radio waves, the beams being narrow and tightly focused. An interstellar laser signal would have to be aimed precisely towards us, an alignment that in and of itself does not resolve all the issues involved. We can take into account the brightness of the transmitting location, working out the parameters for each nearby star and factoring in optical background noise, but we would have no knowledge of the power, aperture and pointing characteristics of a transmitted signal in advance. But if we’re searching for a signal boosted by gravitational lensing, we have a much brighter beam that will have been enhanced for best reception.
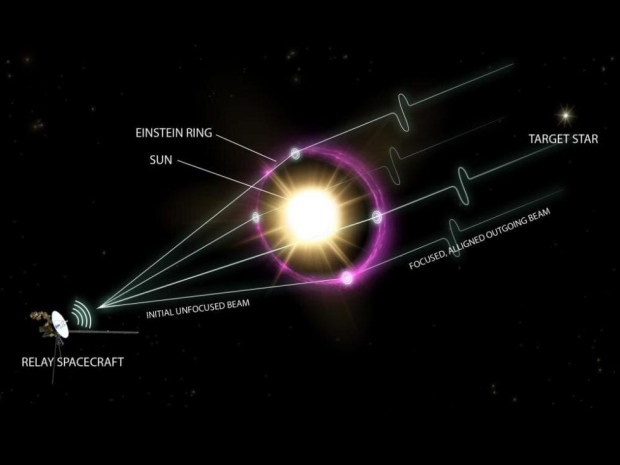
Image: Communications across interstellar distances could take advantage of a star’s ability to focus and magnify communication signals through gravitational lensing. A signal from—or passing through—a relay probe would bend due to gravity as it passes by the star. The warped space around the object acts somewhat like a lens of a telescope, focusing and magnifying the light. Pictured here is a message from our Sun to another stellar system. Possible signals from other stars using these methods could become SETI targets. Image credit: Dani Zemba / Penn State. CC BY-NC-ND 4.0 DEED.
Mathematics at this level is something I admire and find beautiful much in the same way I appreciate Bach, or a stunning Charlie Parker solo. I have nowhere near the skill to untangle it, but take it in almost as a form of art. So I send those more mathematically literate than I am to the paper, while relying on Turyshev’s explanation of the import of these calculations, which seek to determine the shape and dimensions of the lensed caustic, using the results to demonstrate the beam propagation affected by the lens geometry, and the changes to the density of the EM field received.
It’s interesting to speculate on the requirements of any effort to reach another star with a lensed signal. Not only does the civilization in question have to be able to operate within the focal region of its stellar lens, but it has to provide propulsion for its transmitter, given the relative motion between the lens and the target star (our own). In other words, it would need advanced propulsion just to point toward a target, and obviously navigational strategies of the highest order within the transmitter itself. As you can imagine, the same issues emerge within the context of exoplanet imaging. From the paper:
…we find that in optical communications utilizing gravitational lenses, precise aiming of the signal transmissions is also crucial. There could be multiple strategies for initiating transmission. For instance, in one scenario, the transmission could be so precisely directed that Earth passes through the targeted spot. Consequently, it’s reasonable to assume that the transmitter would have the capability to track Earth’s movement. Given this precision, one might question whether a deliberately wider beam, capable of encompassing the entire Earth, would be employed instead. This is just [a] few of many scenarios that merit thorough exploration.
Detecting a lensed signal would demand a telescope network optimized to search for transients involving nearby stars. Such a network would be capable of a broad spectrum of measurements which could be analyzed to monitor the event and study its properties as it develops. Current and near-future instruments from the James Webb Space Telescope and Nancy Grace Roman Space Telescope to the Vera C. Rubin Observatory’s LSST, the Thirty Meter Telescope and the Extremely Large Telescope could be complemented by a constellation of small instruments.
Because the lens parameters are known for each target star, a search can be constructed using a combination of possible transmitter parameters. A search space emerges that relies on current technology for each specific laser wavelength. According to Turyshev’s calculations, a signal targeting a specific spot 1 AU from the Sun would be detectable with such a network with the current generation of optical instruments. Again from the paper:
Once the signal is detected, the spatial distribution of receivers is invaluable, as each will capture a distinct dataset by traveling through the signal along a different path… Correlating the photometric and spectral data from each path enables the reconstruction of the beam’s full profile as it [is] projected onto the solar system. Integrating this information with spectral data from multiple channels reveals the transmitter’s specific features encoded in the beam, such as its power, shape, design, and propulsion capabilities. Additionally, if the optical signal contains encoded information, transmitted via a set of particular patterns, this information will become accessible as well.
While microlensing events created by a signal transmitted through another star’s gravitational lens would be inherently transient, they would also be strikingly bright and should, according to these calculations, be detectable with the current generation of instruments making photometric and spectroscopic observations. Using what Turyshev calls “a spatially dispersed network of collaborative astronomical facilities,” it may be possible not only to detect such a signal but to learn if message data are within. The structure of the point spread function (PSF) of the transmitting lens could be determined through coordinated ground- and space-based telescope observations.
We are within decades of being able to travel to the focal region of the Sun’s gravitational lens to conduct high-resolution imaging of exoplanets around nearby stars, assuming we commit the needed resources to the effort. Turyshev advocates a SETI survey along the lines described to find out whether gravitationally lensed signals exist around these stars, pointing out that such a discovery would open up the possibility of studying an exoplanet’s surface as well as initiating a dialogue. “[W]e have demonstrated the feasibility of establishing interstellar power transmission links via gravitational lensing, while also confirming our technological readiness to receive such signals. It’s time to develop and launch a search campaign.“
The paper is Turyshev, “Search for gravitationally lensed interstellar transmissions,” now available as a preprint. You might also be interested in another recent take on detecting technosignatures using gravitational lensing. It’s Tusay et al., “A Search for Radio Technosignatures at the Solar Gravitational Lens Targeting Alpha Centauri,” Astronomical Journal Vol. 164, No. 3 (31 August 2022), 116 (full text), which led to a Penn State press release from which the image I used above was taken.

Medusa: Deep Space via Nuclear Pulse
The propulsion technology the human characters conceive in the Netflix version of Liu Cixin’s novel The Three Body Problem clearly has roots in the ideas we’ve been kicking around lately. I should clarify that I’m talking about the American version of the novel, which Netflix titles ‘3 Body Problem,’ and not the Chinese 30-part series, which is also becoming available. In the last two posts, I’ve gone through various runway concepts, in which a spacecraft is driven forward by nuclear explosions along its route of flight. We’ve also looked at pellet options, where macroscopic pellets are fired to a departing starship to impart momentum and/or to serve as fusion fuel.

All this gets us around the problem of carrying propellant, and thus offers real benefits in terms of payload capabilities. Even so, it was startling to hear the name Stanislaw Ulam come up on a streaming TV series. Somebody was doing their homework, as Freeman Dyson liked to say. Ulam’s name will always be associated with nuclear pulse propulsion (along with the Monte Carlo method of computation and many other key developments in nuclear physics). It was in 1955 that he and Cornelius Everett performed the first full mathematical treatment of what would become Orion, but the concept goes back as far as Ulam’s initial Los Alamos calculations in 1947.
Image: Physicist and mathematician Stanislaw Ulam. Credit: Los Alamos National Laboratory.
Set off a nuclear charge behind a pusher plate and the craft attached to that plate moves forward. Set off enough devices and you begin to move at speeds unmatched by any other propulsion method, so the deep space concepts that Freeman Dyson, Ted Taylor and team discussed began to seem practicable, including human missions to distant targets like Enceladus. Dyson pushed the concept into the interstellar realm and envisioned an Orion variant reaching Alpha Centauri in just over a century. So detonating devices is a natural if you’re a writer looking for ways to take current technology to deep space in a hurry, as the characters in ‘3 Body Problem’ are.

Johndale Solem’s name didn’t pop up on ‘3 Body Problem,’ but his work is part of the lineage of the interstellar solution proposed there. Solem was familiar with Ted Cotter’s work at Los Alamos, which in the 1970s had explored ways of doing nuclear pulse propulsion without the pusher plate and huge shock absorbers that would be needed for the Orion design. Freeman Dyson explored the concept as well – both he and Cotter were thinking in terms of steel cables unreeled from a spacecraft as it spun on its axis. Dyson would liken the operation to “the arms of a giant squid,” as cables with flattened plates at each end would serve to absorb the momentum of the explosions set off behind the vehicle. Familiar with this work, Johndale Solem took the next step.
Image: Physicist Johndale Solem in 2014. Credit: Wikimedia Commons.
Solem worked at Los Alamos from 1969 to 2000, along the way authoring numerous scientific and technical papers. In the early 1990s, he discussed the design he called Medusa, noting in an internal report that his spacecraft would look something like a jellyfish as it moved through space. He had no interest in Orion’s pusher plate because examining the idea, he saw only problems. For one thing, you couldn’t build a pusher plate big enough to absorb anything more than a fraction of the momentum from the bombs being detonated behind the spacecraft. To protect the crew, the plate and shock absorbers had to be so massive as to degrade performance even more.
The solution: Replace the pusher plate with a sail deployed ahead of the vehicle. The nuclear detonations are now performed between the sail and the spacecraft, driving the vehicle forward. The sail would receive a much greater degree of momentum, and it would be equipped with tethers made so long and elastic that the acceleration would be smoothed out. I quoted Solem some years back on using a servo winch in the vehicle which would operate in combination with the tethers. Let’s look at that again, from the Los Alamos report:
When the explosive is detonated, a motorgenerator powered winch will pay out line to the spinnaker at a rate programmed to provide a constant acceleration of the space capsule. The motorgenerator will provide electrical power during this phase of the cycle, which will be conveniently stored. After the space capsule has reached the same speed as the spinnaker, the motorgenerator will draw in the line, again at a rate programmed to provide a constant acceleration of the space capsule. The acceleration during the draw-in phase will be less than during the pay-out phase, which will give a net electrical energy gain. The gain will provide power for ancillary equipment in the space capsule…
This is hard to visualize, so let’s look at it in two different ways. First, here is a diagram of the basic concept:
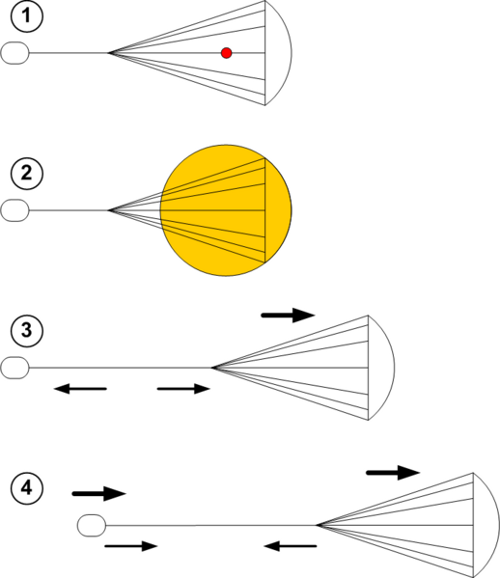
Image: Medusa in operation. Here we see the design 1) At the moment of bomb explosion; 2) As the explosion pulse reaches the parachute canopy; 3) Effect on the canopy, accelerating it away from the explosion, with the spacecraft playing out the main tether with its winch, braking as it extends, and accelerating the vehicle; 4) The tether being winched back in. Imagine all this in action and the jellyfish reference becomes clear. Credit: George William Herbert/Wikimedia.
Second, a video that Al Jackson pointed out to me, made by artist and CGI expert Nick Stevens, shows what Medusa would look like in flight. I recall Solem’s words when I watch this:
One can visualize the motion of this spacecraft by comparing it to a jellyfish. The repeated explosions will cause the canopy to pulsate, ripple, and throb. The tethers will be stretching and relaxing. The concept needed a name: its dynamics suggested MEDUSA.
Bear in mind as you watch, though, that Solem’s Los Alamos report speaks of a 500-meter canopy that would be spin-deployed along with 10,000 tethers. The biggest stress that suggested itself to readers when we’ve discussed Medusa in the past is in the tethers themselves, which is why Solem made them as long as he did. Even so, I became rather enthralled with Medusa early when I first encountered the idea, an interest reinforced by Greg Matloff’s statement (in Deep Space Probes): “Although much analysis remains to be carried out, the Medusa concept might allow great reduction in the mass of a nuclear-pulse starprobe.” With Dyson having given up on Orion, Medusa seemed a way to reinvigorate nuclear pulse propulsion, although to be sure, Dyson’s chief objection to Orion when I talked with him about it was the sheer impracticality of the concept, an issue which surely would apply to Medusa as well.
Like so much in the Netflix ‘3 Body Problem,’ the visuals of the bomb runway sequence are well crafted. In fact, I find Liu Cixin’s trilogy so stuffed with interesting ideas that my recent re-reading of The Three Body Problem and subsequent immersion in the following two novels have me wanting to explore his other work. I haven’t yet attempted the Chinese series, which is longer and presents the daunting prospect of dealing with a now familiar set of plot elements with wholly different actors. I’ll need to dip into it as Netflix ponders a second season for the American series.
Anyway, notice the interesting fact that what you have as a propulsion method on ‘3 Body Problem’ is essentially Medusa adapted to a nuclear bomb runway, with the sail-driven craft intercepting a series of nuclear weapons. As each explodes, the spacecraft is pushed to higher and higher velocities. I’m curious to know how the Chinese series handles this aspect of the story, and also curious about who introduced this propulsion concept, which I still haven’t located in the novels. I’m not aware of a fusion runway combined with a sail anywhere in the interstellar literature. Nice touch!
The Los Alamos report I refer to above is Solem’s “Some New Ideas for Nuclear Explosive Spacecraft Propulsion,” LA-12189-MS, October 1991 (available online). Solem also wrote up the Medusa concept in “Medusa: Nuclear Explosive Propulsion for Interplanetary Travel,” JBIS Vol. 46, No. 1 (1993), pp. 21-26. Two other JBIS papers also come into play for specific mission applications: “The Moon and the Medusa: Use of Lunar Assets in Nuclear-Pulse Propelled Space Travel,” JBIS Vol. 53 (2000), pp. 362-370 and “Deflection and Disruption of Asteroids on Collision Course with Earth,” JBIS Vol. 53 (2000), pp. 180-196. To my knowledge, Freeman Dyson’s ‘The Bolo and the Squid,’ a 1958 memo at Los Alamos treating these concepts, remains classified.

Fusion Pellets and the ‘Bussard Buzz Bomb’
Fusion runways remind me of the propulsion methods using pellets that have been suggested over the years in the literature. Before the runway concept emerged, the idea of firing pellets at a departing spacecraft was developed by Clifford Singer. Aware of the limitations of chemical propulsion, Singer first studied charged particle beams but quickly realized that the spread of the beam as it travels bedevils the concept. A stream of macro-pellets, each several grams in size, would offer a better collimated ‘beam’ that would vaporize to create a hot plasma thrust when it reaches the spacecraft.

Even a macro-pellet stream does ‘bloom’ over time – i.e., it loses its tight coherency because of collisions with interstellar dust grains – but Singer was able to show through papers in The Journal of the British Interplanetary Society that particles over one gram in weight would be sufficiently massive to minimize this. In any case, collimation could also be ensured by electromagnetic fields sustained by facilities along the route that would measure the particles’ trajectory and adjust it.
Image: Clifford Singer, whose work on pellet propulsion in the late 1970s has led to interesting hybrid concepts involving on-board intelligence and autonomy. Credit: University of Illinois.
Well, it was a big concept. Not only did Singer figure out that it would take a series of these ‘facilities’ spaced 340 AU apart to keep the beam tight (he saw them as being deployed by the spacecraft itself as it accelerated), but it would also take an accelerator 105 kilometers long somewhere in the outer Solar System. That sounds crazy, but pushing concepts forward often means working out what the physics will allow and thus putting the problem into sharper definition. I’ve mentioned before in these pages that we have such a particle accelerator in the form of Jupiter’s magnetic field, which is fully 20,000 times stronger than Earth’s.
We don’t have to build Jupiter, and Mason Peck (Cornell University) has explored how we could use its magnetic field to accelerate thousands of ‘sprites’ – chip-sized spacecraft – to thousands of kilometers per second. Greg Matloff has always said how easy it is to overlook interstellar concepts that are ‘obvious’ once suggested, but it takes that first person to suggest them. Going from Singer’s pellets to Peck’s sprites is a natural progression. Sometimes nature steps in where engineering flinches.
The Singer concept is germane here because the question of fusion runways depends in part upon whether we can lead our departing starship along so precise a trajectory that it will intercept the fuel pellets placed along its route. Gerald Nordley would expand upon Singer’s ideas to produce a particle stream enlivened with artificial intelligence, allowing course correction and ‘awareness’ at the pellet level. Now we have a pellet that is in a sense both propellant and payload, highlighting the options that miniaturization and the growth of AI have provided the interstellar theorist.
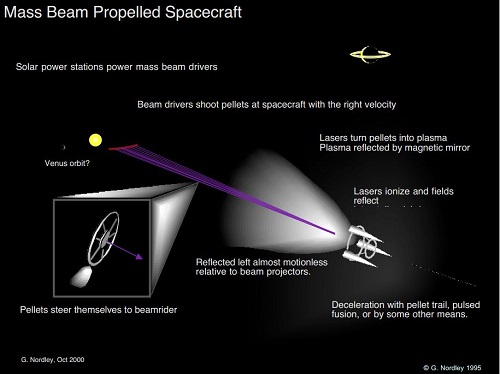
Image: Pushing pellets to a starship, where the resulting plasma is mirrored as thrust. Nordley talks about nanotech-enabled pellets in the shape of snowflakes capable of carrying their own sensors and thrusters, tiny craft that can home in on the starship’s beacon. Problems with beam collimation thus vanish and there is no need for spacecraft maneuvering to stay under power. Credit: Gerald Nordley.
Jordin Kare’s contributions in this realm were striking. A physicist and aerospace engineer, Kare spent years at Lawrence Livermore National Laboratory working on early laser propulsion concepts and, in the 1980s, laser-launch to orbit, which caught the attention of scientists working in the Strategic Defense Initiative. He would go on to become a spacecraft design consultant whose work for the NASA Institute for Advanced Concepts (as it was then called) analyzed laser sail concepts and the best methods for launching such sails using various laser array designs.
Kare saw ‘smart pellets’ in a different light than previous researchers, thinking that the way to accelerate a sail was to miniaturize it and bring it up to a percentage of c close to the beamer. This notion reminds me of the Breakthrough Starshot sail concept, where the meter-class sails are blasted up to 20 percent of lightspeed within minutes by a vast laser array. But Kare would have nothing to do with meter-class sails. His notion was to make the sails tiny, craft them out of artificial diamond (he drew this idea from Robert Forward) and use them not as payload but as propulsion. His ‘SailBeam’, then, is a stream of sails that, like Singer’s pellets, would be vaporized for propulsion as they arrived at a departing interstellar probe.

Kare was a character, to put it mildly. Brilliant at what he studied, he was also a poet well known for his ‘filksongs,’ the science fiction fandom name for SF-inspired poetry, which he would perform at conventions. His sense of humor was as infectious as his optimism. Thus his DIHYAN, a space launch concept involving reusable rockets (if he could only see SpaceX’s boosters returning after launch!). DIHYAN, in typical Kare fashion, stood for “Do I Have Your Attention Now?” Kare’s role in the consideration of macro-scale matter sent for propulsion is secure in the interstellar literature.
And by the way, when I write about Kare, I’m always the recipient of email from well-meaning people who tell me that I’ve misspelled his name. But no, ‘Jordin’ is correct.
We need to talk about SailBeam at greater length one day soon. Kare saw it as “the most engineering-practical way to get up to a tenth of the speed of light.” It makes sense that a mind so charged with ideas should also come up with a fusion runway that drew on his SailBeam thinking. Following on to the work of Al Jackson, Daniel Whitmire and Greg Matloff, Kare saw that if you could place pellets of deuterium and tritium carefully enough, a vehicle initially moving at several hundreds of kilometers per second would begin encountering them with enough velocity to fire up its engines. He presented the idea at a Jet Propulsion Laboratory workshop in the late 1980s.
We’re talking about an unusual craft, and it’s one that will resonate not only with Johndale Solem’s Medusa, which we’ll examine in the next post, but also with the design shown in the Netflix version of Liu Cixin’s The Three Body Problem. This was not the sleek design familiar from cinema starships but a vehicle shaped more or less like a doughnut, although a cylindrical design was also possible. Each craft would have its own fusion pellet supply, dropping a pellet into the central ‘hole’ as one of the fusion runway pellets was about to be encountered. Kare worked out a runway that would produce fusion explosions at the rate of thirty per second.
Like Gerald Nordley, Kare worried about accuracy, because each of the runway pellets has to make a precise encounter with the pellet offered up by the starship. When I interviewed him many years back, he told me that he envisioned laser pulses guiding ‘smart’ pellets. Figure that you can extract 500 kilometers per second from a close solar pass to get the spacecraft moving outward at sufficient velocity (a very optimistic assumption, relying on materials technologies that are beyond our grasp at the moment, among other things), and you have the fusion runway ahead of you.
Initial velocity is problematic. Kare believed the vehicle would need to be moving at several hundreds of kilometers per second to attain sufficient velocity to begin firing up its main engines as it encountered the runway of fusion pellets. Geoff Landis would tell me he thought the figure was far too low to achieve deuterium/tritium ignition. But if it can be attained, Kare’s calculations produced velocities of 30,000 kilometers per second, fully one-tenth the speed of light. The fusion runway would extend about half a light day in length, and the track would run from near Earth to beyond Pluto’s orbit.
And there you have the Bussard Buzz Bomb, as Kare styled it. The reference is of course to the German V-1, which made a buzzing, staccato sound as it moved through English skies that those who heard it would come to dread, because when the sound stopped, you never knew where it would fall. You can’t hear anything in space, but if you could, Kare told me, his starship design would sound much like the V-1, hence the name.
In my next post, I’ll be talking about Johndale Solem’s Medusa design, which uses nuclear pulse propulsion in combination with a sail in startling ways. Medusa didn’t rely on a fusion runway, but the coupling of this technology with a runway is what started our discussion. The Netflix ‘3 Body Problem’ raised more than a few eyebrows. I’m not the only one surprised to see the wedding of nuclear pulse propulsion, sails and runways in a single design.
Clifford Singer’s key paper is “Interstellar Propulsion Using a Pellet Stream for Momentum Transfer,” JBIS 33 (1980), pp. 107-115. He followed this up with “Questions Concerning Pellet-Stream Propulsion,” JBIS 34 (1981), pp. 117-119. Gerald Nordley’s “Interstellar Probes Propelled by Self-steering Momentum Transfer Particles” (IAA-01-IAA.4.1.05, 52nd International Astronautical Congress, Toulouse, France, 1-5 Oct 2001) offers his take on self-guided pellets. Jordin Kare’s report on SailBeam concepts is “High-Acceleration Micro-Scale Laser Sails for Interstellar Propulsion,” Final Report, NIAC Research Grant #07600-070, revised February 15, 2002 and available here. You might also enjoy my SailBeam: A Conversation with Jordin Kare.

The Interstellar Fusion Runway Evolves
Let’s talk about how to get a spacecraft moving without onboard propellant. As noted last week, this is apropos of the design shown in the Netflix streaming video take on Liu Cixin’s novels, which the network titles ‘3 Body Problem.’ There, a kind of ‘runway’ is conceived, one made up of nuclear weapons that go off in sequence to propel a sail and its payload. The plan is to attain 0.012 c and reach an oncoming fleet that is headed to Earth but will not arrive for another four centuries.
This is an intriguing notion, and one with echoes in the interstellar literature. Because Johndale Solem mixed sails and nuclear weapons in a design called ‘Medusa’ that he described in a Los Alamos report back in 1991, although its roots go back decades earlier, as I’ll discuss in an upcoming article. Mixing sails, nuclear weapons and a fusion runway is an unusual take, a hybrid concept that caught my eye immediately, as it did that of Al Jackson, who alluded to runways in a paper in the 1970s. I’ve just become aware of a Greg Matloff paper from 1979 on runways as well.
So let’s start with the runway concept and in subsequent posts, I will be looking at how Medusa evolved and consider whether the hybrid concept of ‘3 Body Problem’ is worth pursuing. Jackson’s paper, written with Daniel Whitmire, is one we’ve considered before in these pages. The concept is to power up a starship by a laser but use reaction mass gathered from the interstellar medium, collecting the latter with a ramscoop. Here the model draws on Robert Bussard’s ramjet notions, originally published in 1960 and more or less immortalized in Poul Anderson’s novel Tau Zero. Jackson and Whitmire’s version was one of several variants on Bussard’s original concept and offered a number of performance benefits.

Image: The interstellar ramjet, as envisioned by British artist Adrian Mann. Variants have appeared in the literature to get around the drag issue induced by the ramscoop design. A fusion runway seeds fuel along a track that the craft follows as it accelerates.
You’ll notice that this is also a hybrid concept, combining ramjet capabilities with laser beaming. Lasers had already been considered for beaming a terrestrial or Solar System-based laser at the departing craft, which could deploy a lightsail to draw momentum from the incoming photons. Jackson and Whitmire found the latter method inefficient. Their solution was to beam the laser at a ramjet that would use reaction mass obtained from a Bussard-style magnetic ram scoop. The ramjet uses the laser beam as a source of energy but, unlike the sail, not as a source of momentum.
Jackson and Whitmire were a potent team, and this is one of their best papers. These methods could be used to reach 0.14 c, allowing the vehicle to switch into full ramjet mode at that point. And because the laser is a source of energy rather than momentum, it can also be used as a means to decelerate on the return trip. For our purposes today, I turn to the last part of the paper, which outlines other starship concepts that grow out of the laser beaming analysis. Here is the relevant passage:
Another possibility would be to artificially make a fusion ramjet runway. Micron-size frozen deuterium pellets could be accelerated electrostatically or electromagnetically beginning several years prior to take-off at which time a fusion ramjet with a relatively modest scoop cross section (perhaps a physical structure) would begin acceleration.
So we have a spacecraft that collects its fuel along the way. As opposed to the ‘pure’ ramjet, which scoops up interstellar material and is dependent on the medium through which it moves, this fusion runway ramjet would know exactly the trajectory to take to collect the needed fuel pellets as it accelerates. Bear in mind the original Bussard ramjet problem of having to reach a certain percentage of lightspeed before being able to ignite its fusion engine. Problem solved.
In recent correspondence, Jackson pointed out that the idea harkens back to the German Vergeltungswaffe 3 (“Vengeance Weapon 3”), which was a gun originally designed to bombard London but only saw use against Allied targets in Luxembourg in 1945 (the bunkers at the Pas-de-Calais were destroyed by bombing raids). Multiple solid-fuel rocket boosters were ignited by the gases pushing the projectile as it moved in staged fashion through the barrel. The French Army had considered plans for such a staged cannon as far back as 1918, and the idea dates to the 19th Century.

Image: The prototype V-3 cannon at Laatzig, Germany (now Zalesie, Poland) in 1942. Credit: Bundesarchiv, Bild 146-1981-147-30A / CC-BY-SA 3.0.
Greg Matloff picked up on the Jackson and Whitmire paper in a 1979 paper in The Journal of the British Interplanetary Society which he was kind enough to pass along to me. The Jackson/Whitmire fusion runway would, he believed, improve ramjet performance and alleviate aerodynamic drag, which is a problem that sharply reduces a Bussard vehicle’s acceleration. He considered in the paper a fusion fuel released as fuel pellets moving in the direction of the destination star, with the ramjet moving up from behind to capture and fuse the pellets. In one scenario, tanker craft would be launched over a 50 year period to produce a runway 0.1 light years long.
Matloff as well as Jackson and Whitmire considered other variations on the interstellar ramjet idea, and I want to just mention these before moving on. From the Matloff paper:
As Whitmire and Jackson have mentioned, the performance of a ramjet might be of interest just above the photosphere of the Sun, n a high-energy, high-particle environment. More prosaically, a ramscoop could be utilized near the Earth to collect fusion fuel from the solar wind over a few decades. Then, if the fuel is utilized to power a ram-augmented interstellar rocket (RAIR), such an approach might be competitive in any discussion of the difficulties and merits of the various ramjet derivatives.
A Sun-skimming ramjet is one I had never seen discussed until I read Jackson and Whitmire. It would make for a lively hard SF tale, that’s for sure. Given the problems with ramjet drag that have been wrestled with in the subsequent literature, it’s worth considering Matloff’s idea of solar wind fuel collection at much lower speeds in the inner system. In any case, the fusion runway notion offers one way to collect a known supply of fuel over the length of a runway that would launch an interstellar craft.
When I wrote my Centauri Dreams book early in the century, I was unaware of both the papers we’ve looked at today, and focused on the only runway concept that was then known to me, the so-called ‘Bussard Buzz Bomb’ of the free-thinking Jordin Kare. Kare is, alas, no longer with us, but I enjoyed a long conversation with him on his runway concept, and I want to cover that in the next post before moving on to Johndale Solem’s Medusa.
The Jackson/Whitmire paper on laser-powered ramjets is “Laser Powered Interstellar Ramjet,” Journal of the British Interplanetary Society Vol. 30 (1977), 223-226. Al Jackson: A Laser Ramjet Reminiscence presents Al’s thoughts on this paper as written for this site. Greg Matloff’s paper on fusion runways is “The Interstellar Ramjet Acceleration Runway,” JBIS Vol. 32 (1979), 219-220. The ToughSF site offers a detailed explanation of runway concepts in Fusion Highways in Space.

Interstellar Propulsion in ‘3 Body Problem’
You never know when a new interstellar propulsion concept is going to pop up. Some of us have been kicking around fusion runway ideas, motivated by Netflix’s streaming presentation of the Liu Cixin novel The Three Body Problem. There Earth is faced with invasion from an extraterrestrial civilization, but with centuries to solve the problem because it will take that long for the fleet to arrive. Faced with the need to get as much information as possible about the invaders, scientists desperately search for a way to get human technology up to 1.2 percent of lightspeed to intercept the fleet.

Image: 20 different examples of periodic solutions to the three body problem. Credit: Perosello/Wikimedia Commons. CC BY-SA 4.0.
So how would you do that with technology not much more advanced than today’s? The Netflix show’s solution is ingenious, though confusing for those who assume that the Netflix ‘3 Body Problem’ is based solely on the first of the Cixin novels. Actually it edges into the rest of the trilogy, which includes 2008’s The Dark Forest and 2010’s Death’s End. The whole sequence is known as Remembrance of Earth’s Past, and I had to dig into not just The Three Body Problem but The Dark Forest to find much discussion of any kind of propulsion.
Now we’re in a dark wood indeed. For in The Dark Forest (the title is an allusion to the Fermi paradox, usually linked with concerns over METI), the idea of a precursor scouting of the alien invasion fleet does not appear, nor does it appear in the first novel. What we do get is a lot of confusing discussion, such as this:
“If controlled nuclear fusion is achieved, spacecraft research will begin immediately. Doctor, you know about the two current research forks: media-propelled spacecraft and non-media radiation-drive spacecraft. Two opposing factions have formed around these two directions of research: the aerospace faction advocates research into media-propelled spacecraft, while the space force is pushing radiation-drive spacecraft… The fusion people and I are in favor of the radiation drive. For my part, I feel that it’s the only plan that enables interstellar cosmic voyages.”
The book’s many references to a ‘radiation drive’ seem to be referring to antimatter. What Cixin calls ‘media-propelled spacecraft’ is opaque to me, and I’d welcome reader comments on what it represents. Then there is a ‘curvature drive’ that appears in the final volume of the trilogy, but let’s leave that out of the discussion today. Perhaps it’s a kind of Alcubierre concept, but in any case I want to focus on fusion runways and sails for now, because the Netflix eight-part video presents the idea of sending a relatively small payload toward the invasion fleet using a form of nuclear pulse propulsion.
Here the presentation is accurate if rudimentary but the idea is fascinating. Because I don’t find this in the novels, I am wondering about where, along the route to production, the show acquired a technology made famous originally by Project Orion, with its sequence of nuclear explosions visualized as occurring behind a spacecraft’s huge shock absorbers. Wonderfully, the idea opens up to multiple interstellar propulsion ideas in the literature, including Johndale Solem’s Medusa concept and various fusion runway notions that emerged decades ago, one by my friend Al Jackson and Daniel Whitmire, another by Jordin Kare, who christened his concept the ‘Bussard buzz bomb.’
So we’ve got a lot to talk about. And out of the blue Adam Crowl wrote to remind me of something Martyn Fogg pointed out in 2017, when I wrote about Medusa then. Here’s Martyn’s comment:
Suppose these Solem sails were to have a small hole in their centre, they could be steered accurately, and that nuclear propulsion charges could be lined up perfectly in space, perhaps by laser guidance. Then one might imagine an ‘Interstellar Solem Sail Runway’ which would impart a jolt of pulse propulsion each time its sail overtook each charge, thereby accelerating the outgoing ship as a whole up to interstellar cruse velocity. The vessel would only need fuel to decelerate at the target system: a considerable reduction in the mass it would need to carry.
Talk about prescient! Because this is what shows up on the Netflix series.
I’m slammed for time this morning and have way too many ideas floating around as well as tabs open in various screens, so I’m going to break here and pick up this discussion next week, when I want to get into the details of fusion runways, and then I want to relate all this to Solem’s Medusa work by way of illustrating not only how ingenious all these ideas are, but how striking the design in the screen version of the Three Body Problem turns out to be. The designs we’ll be discussing are some of the most innovative that have come out of the interstellar effort thus far.

Deep Space Trajectories: Exiting the Heliosphere
Eugene Parker, after whom the Parker Solar Probe was named, seems to have been the first to have accurately predicted the stream of particles emitted by the Sun that forms the ‘solar wind.’ Parker made the call in a 1958 paper, when solar sailing was just being noised about for the first time, so it wouldn’t have struck him that the term was a bit incautious. Today, when solar sailing is operational, people often assume the solar wind drives solar sails, when in fact the operating principle for solar sails is the momentum generated by photons, which are themselves massless. But streaming particles are indeed a kind of ‘wind,’ and there are magnetic sail concepts tailored for them too.
As always, we have to be careful about terminology, especially given the significance of the solar wind in defining our Solar System’s environment. Solar transients likewise have to be considered, because in addition to solar flares, we have to factor in coronal mass ejections (CMEs) and the particles accelerated by both of these. All of this as well as the interplanetary magnetic field shapes our star’s interactions with the local interstellar medium, creating the plasma envelope called the heliosphere. Only the Voyager spacecraft have returned data from the LISM, and they’re not very far into it.
We’ve looked at the Interstellar Probe concept in these pages before. The result of countless hours and numerous contributors at the Johns Hopkins Applied Physics Laboratory and elsewhere, the study was created for the Solar and Space Physics Decadal Survey and extensively analyzes everything from the launch vehicle to instrumentation for a mission that would exit the heliosphere and reach as far as hundreds of AUs within 50 years. Given that our knowledge of the realm beyond the heliosphere is almost entirely the result of remote sensing and indirect measurements, having an actual spacecraft on the scene would take us far beyond our modeling.
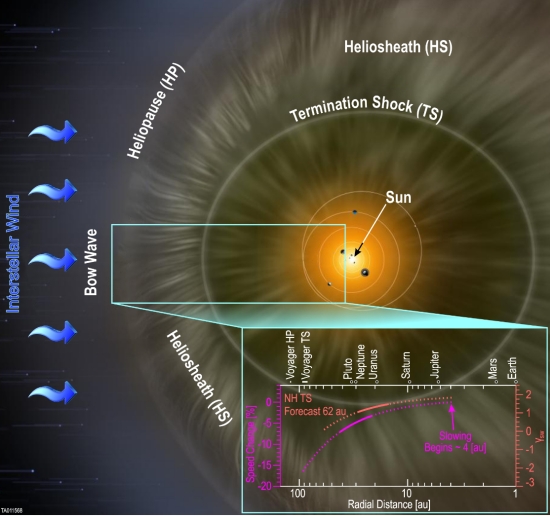
Image: The SWAP instrument aboard New Horizons has confirmed that the solar wind slows as it travels farther from the Sun. This schematic of the heliosphere shows that the solar wind begins slowing at approximately 4 AU radial distance from the Sun and continues to slow as it moves toward the outer solar system and picks up interstellar material. Current extrapolations reveal the termination shock may currently be closer than found by the Voyager spacecraft. However, increasing solar activity will soon expand the heliosphere and push the termination shock farther out, possibly to the 84-94 AU range encountered by the Voyager spacecraft. Credit: Southwest Research Institute; background artist rendering by NASA and Adler Planetarium.
Because I’m talking about the outer boundaries of the heliosphere today, a quick word about how remote sensing ‘sees’ them is appropriate. We have data from the IBEX satellite (Interstellar Boundary Explorer) covering an entire solar cycle from 2009 through 2019. Although it’s in Earth orbit, IBEX detects energetic neutral atoms (ENAs) from the outer regions of the heliosphere, the zone where solar wind particles begin to collide with those of the even less understood interstellar wind. We are in essence mapping a region by sending a signal – actually using the Sun’s ‘signal,’ the particles of the solar wind – deep into the edge of the system and trying to make sense out of the return echoes. The IMAP (Interstellar Mapping and Acceleration Probe), set for launch in 2025, will further examine this region from its own vantage at the L1 Lagrange point.
We can draw a lot of conclusions from the data from such missions, but not enough. Sarah Spitzer (University of Michigan), lead author of a paper on a just released study that analyzes how best to exit the heliosphere, notes the significance of the JHU/APL work: “Without such a mission, we are like goldfish trying to understand the fishbowl from the inside.”
Indeed. Considered as a kind of shield, the heliosphere acts as a brake on galactic radiation, but predicting its effects, and even more significantly its shape and size over time, is all but impossible. We tend to refer to the heliosphere as a ‘bubble,’ but it’s a poor term given that the shape changes with solar output and interactions with the LISM. A variety of potential shapes for the heliosphere remain in play in the literature. Have a look at the figure below, which represents just one of the numerous possibilities.
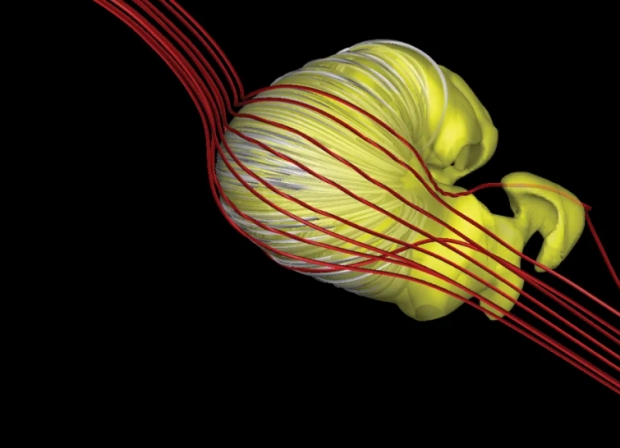
Image: One recent study of the heliosphere’s shape posited a croissant-shape or small spherical shape with tail lobes. Credit: Figure adapted from Merav Opher et al., 2020.
As Spitzer and colleagues note:
Small variations in model parameters and properties measured in the nose of the heliosphere, the leading edge in the direction of the Sun’s motion through the LISM, lead to significant differences in the projected shape. The global response of the heliosphere is additionally expected to fluctuate with solar activity and therefore solar cycle…, which is yet another element in the interplay of heliosphere–interstellar interactions and another factor in our uncertainty of the overall shape. The main features of the shape of the heliosphere include the nose; the tail, which can be defined relative to the Sun as the region of the heliosphere found in the direction opposite the Sun’s motion through the LISM; the size of the heliosphere; and the behavior of the magnetic field lines at the heliospheric boundaries. All of these properties, including the size of the heliosphere, vary vastly in different proposed shapes and models of the heliosphere, which range in size anywhere from hundreds to thousands of au and in shape from comet- or magnetosphere-like or otherwise with extended tails… to spherical to croissant-shaped with multiple tail lobes…
Bear in mind that the heliosphere is a moving target. As recently as 60,000 years ago, the Sun entered what is called the Local Interstellar Cloud, and is now considered to be at that cloud’s edge or perhaps beyond it and in contact with surrounding clouds. The JHU/APL Interstellar Probe study notes that within 2000 years, our system will likely be within a completely different interstellar environment. The heliosphere will adjust. Let me quote the Interstellar Probe report on this, because the effects are startling when we consider the Sun’s 20 revolutions around the galactic core since its formation:
The orders-of-magnitude differences in interstellar properties have had dramatic consequences for the penetration of interstellar gas, dust, and galactic cosmic rays (GCRs) that have affected elemental and isotopic abundances, chemical atmospheric evolution, and perhaps even biological evolution. Along the evolutionary path, high interstellar cloud densities and ionization fractions have likely compressed the heliosphere down to below 25 au… Evidence is emerging for supernovae explosions as recent as 3 million years ago at only 20–50 pc from the Sun that probably compressed the heliosphere even below the orbit of Saturn and perhaps more, exposing the terrestrial planets to almost the full force of interstellar material and GCRs…
The GCR’s referenced above are galactic cosmic rays, high energy particles and heavy nuclei that can prove lethal to biology. The shielding effects of the heliosphere are all too easy to take for granted until we consider its malleable nature, so the more we learn about what affects it the better. The JHU/APL work highlights a probe trajectory that will not only sample the local interstellar medium but give us the ‘look back’ capability to see it as a whole, with the probe exiting the heliosphere at approximately 45 degrees off the heliopause nose direction.
This trajectory is attractive because it allows the heliopause and local interstellar medium to be reached within a reasonable timeframe, which in this context means something less than 50 years with current propulsion technologies. It also offers what the authors call “somewhat of a side view of the heliopause,” though one in the direction of the nose, and it allows the IBEX ribbon, a still puzzling region of enhanced Energetic Neutral Atom (ENA) emission in the outer heliosphere, to be probed.
But a trajectory through the IBEX ribbon center is only one of those that Spitzer and team analyze, ranging from the heliosphere nose to various angles out of the heliotail, the trailing part of the heliosphere in relation to the Sun’s motion through the medium. Here again I’m reminded of how little we know of the heliosphere’s shape, for some estimates of the heliotail have it extending more than 5000 AU downwind of the Sun. Hence the value of this paper, which assembles what our indirect observing methods have so far produced by way of data on the various defined parts of the heliosphere.
To facilitate mission planning, the paper proposes continued indirect measurements of ENA and the pickup ions (PUI) that facilitate a stronger ENA flux, emphasizing the heliotail, and measurements of interstellar ions that penetrate the heliosphere, including cosmic rays in the heliotail region. For the in situ measurements, the authors point out that the largest differences between the suggested shapes of the heliosphere would appear in the tail region. Our probe would thus do best to exit through the side of the heliosphere’s tail. Better still, the authors say, would be a two-spacecraft Interstellar Probe mission option reminiscent of the twin Voyager missions, one moving toward the nose, the other in the direction of the heliotail.
A great idea, but try to get that through the various funding entities… Even so:
Only a study of the tailward region of the heliosphere will give definitive evidence for the complete shape, which impacts how the heliosphere interacts with the LISM and therefore how the LISM impacts the composition of the heliosphere. Therefore, complementary in situ and indirect interstellar measurements must be made tailward within the heliosphere. These measurements can be made through the use of intentional instrumentation requirements for outer heliosphere missions. Additionally, it would be beneficial for the Interstellar Probe mission to either consider a trajectory through the heliotail, via the flank, or to comprise a unified mission of two spacecraft, in which a second Interstellar Probe would be launched with a tailward trajectory, perhaps intersecting one of the proposed…tail lobes.
The paper is Spitzer et al, “Complementary interstellar detections from the heliotail,” Frontiers in Astronomy and Space Sciences (08 February 2024). Full text.


